2025-04-10：选择矩阵中单元格的最大得分。用go语言，给你一个由正整数构成的二维矩阵 grid。 你的任务是从这个矩阵中选择一个或多个单元格，满足以下条件： 1.被选的单元格不能来自同一行。_goland grid

2025-04-10：选择矩阵中单元格的最大得分。用go语言，给你一个由正整数构成的二维矩阵 grid。

你的任务是从这个矩阵中选择一个或多个单元格，满足以下条件：

1.被选的单元格不能来自同一行。

2.选中的单元格的值必须互不相同。

你需要计算所选单元格值的总和，并返回可以获得的最大得分。

1 <= grid.length, grid[i].length <= 10。

1 <= grid[i][j] <= 100。

输入： grid = [[1,2,3],[4,3,2],[1,1,1]]。

输出： 8。

解释：

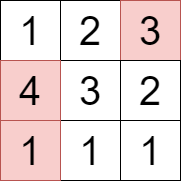
选择上图中用彩色标记的单元格，对应的值分别为 1、3 和 4 。

题目来自leetcode3276。

解题步骤描述

1. 解析输入矩阵：

   • 给定一个二维矩阵 grid，由正整数组成。首先，我们需要了解这个矩阵的结构以及其中的数字。

2. 构建位置映射：

   • 创建一个映射 pos，用于存储每个正整数值在矩阵中出现的行号。这里我们用位操作来记录行号。例如，如果数字 x 出现在第 i 行，则在 pos[x] 中的 i 位置会被设置为 1（通过位运算记录）。

3. 构建图结构：

   • 将问题转化为图论中的最大流（或最小费用流）问题。图由源点 S，目标点 T 以及中间的数字节点和行节点组成。
   • 每个唯一的数字 x 会对应一个节点，数字节点与行节点之间有边，表示该数字可以在某一行中被选中。
   • 从源点 S 到每个数字节点的边容量为 1，边的花费为 -x（用来表示选择这个数字的得分）。
   • 每个行节点到目标点 T 之间也有边，容量为 1。

4. SPFA算法实现最短路径学习：

   • 通过 SPFA（Shortest Path Faster Algorithm）算法来计算从源点 S 到目标点 T 的最短路径，这是一个动态更新路径成本的过程。
   • 每次找到一条有效路径后，更新边的流量。此时，要确保所选的数字未在同一行中。

5. 流量调整：

   • 在找到一条有效路径后，计算最大流量 minF（这条路径上的流量最小值）。
   • 根据路径更新每条边的流量，确保选择的数字互不相同且不在同一行。

6. 计算总得分：

   • 每次找到路径后，根据路径的成本更新总得分，最终得到选中数字的最大得分。

时间复杂度与空间复杂度分析

• 时间复杂度：

  • 假设 n 是矩阵的行数，m 是列数。构建位置映射和图结构的复杂度为 O(n * m)，而 SPFA 的最坏时间复杂度为 O(VE)，其中 V 是图的节点数量，E 是图的边数量。由于节点总数为 O(n * max_value)，边的数量也与节点数量成正比，因此总复杂度为 O(n * m * (nm + max_value))，可简化为 O(n^2 * m) 或类似的表达根据具体实现。

• 空间复杂度：

  • 在构建图时，存储边的列表也需要 O(V + E) 的空间，最终可以认为空间复杂度是 O(n * max_value + n + m)，其中 n * max_value 是存储所有数字的并行性，而 n、m 是行列的总数，简化后可视作 O(n * max_value)。

综上所述，此算法在小规模矩阵（1 <= grid.length, grid[i].length <= 10）的条件下表现良好，能够高效解决选取单元格的最大得分问题。

Go完整代码如下：

package mainimport (\"fmt\"\"math\"\"math/bits\")func maxScore(grid [][]int) int {pos := map[int]int{}for i, row := range grid {for _, x := range row {// 保存所有包含 x 的行号（压缩成二进制数）pos[x] |= 1 << i}}// 建图k := len(pos)m := len(grid)// rid 为反向边在邻接表中的下标type neighbor struct{ to, rid, cap, cost int }g := make([][]neighbor, k+m+2)addEdge := func(from, to, cap, cost int) {g[from] = append(g[from], neighbor{to, len(g[to]), cap, cost})g[to] = append(g[to], neighbor{from, len(g[from]) - 1, 0, -cost})}S := k + mT := k + m + 1i := 0for x, posMask := range pos {for t := uint(posMask); t > 0; t &= t - 1 {j := bits.TrailingZeros(t)addEdge(i, k+j, 1, 0)}addEdge(S, i, 1, -x)i++}for j := range grid {addEdge(k+j, T, 1, 0)}// 下面是费用流模板dis := make([]int, len(g))type vi struct{ v, i int }fa := make([]vi, len(g))inQ := make([]bool, len(g))spfa := func() bool {for i := range dis {dis[i] = math.MaxInt}dis[S] = 0inQ[S] = trueq := []int{S}for len(q) > 0 {v := q[0]q = q[1:]inQ[v] = falsefor i, e := range g[v] {if e.cap == 0 {continue}w := e.tonewD := dis[v] + e.costif newD < dis[w] {dis[w] = newDfa[w] = vi{v, i}if !inQ[w] {inQ[w] = trueq = append(q, w)}}}}// 循环结束后所有 inQ[v] 都为 false，无需重置return dis[T] < math.MaxInt}minCost := 0for spfa() {minF := math.MaxIntfor v := T; v != S; {p := fa[v]minF = min(minF, g[p.v][p.i].cap)v = p.v}for v := T; v != S; {p := fa[v]e := &g[p.v][p.i]e.cap -= minFg[v][e.rid].cap += minFv = p.v}minCost += dis[T] * minF}return -minCost}func main() {grid := [][]int{{1, 2, 3}, {4, 3, 2}, {1, 1, 1}}results := maxScore(grid)fmt.Println(results)}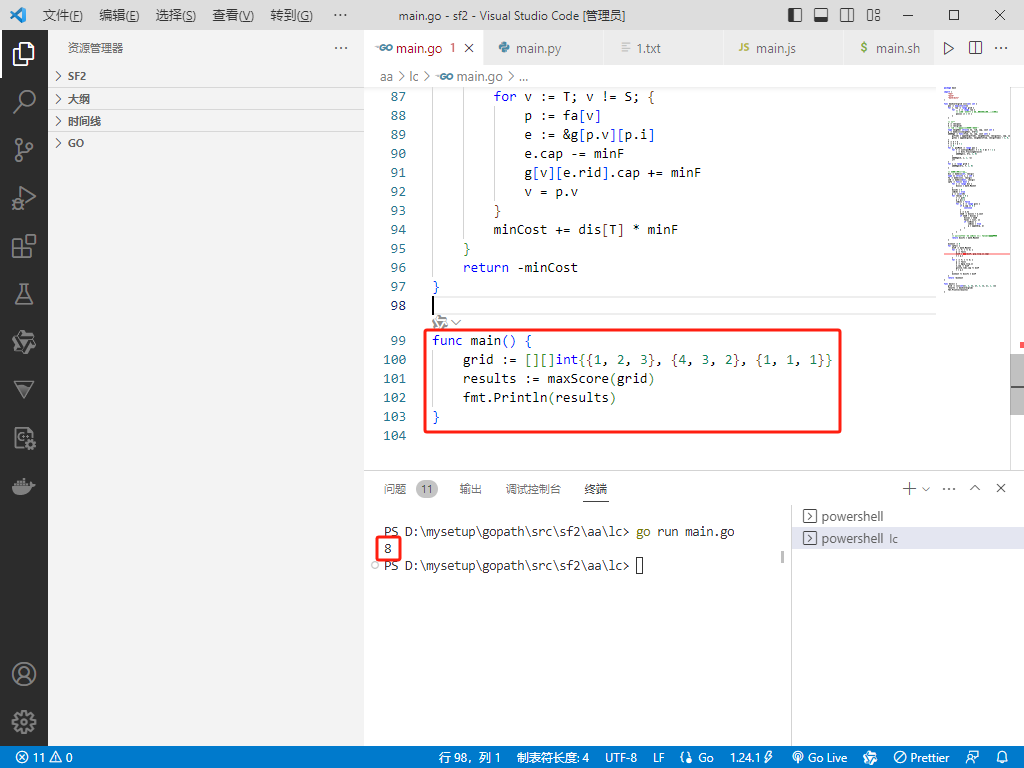

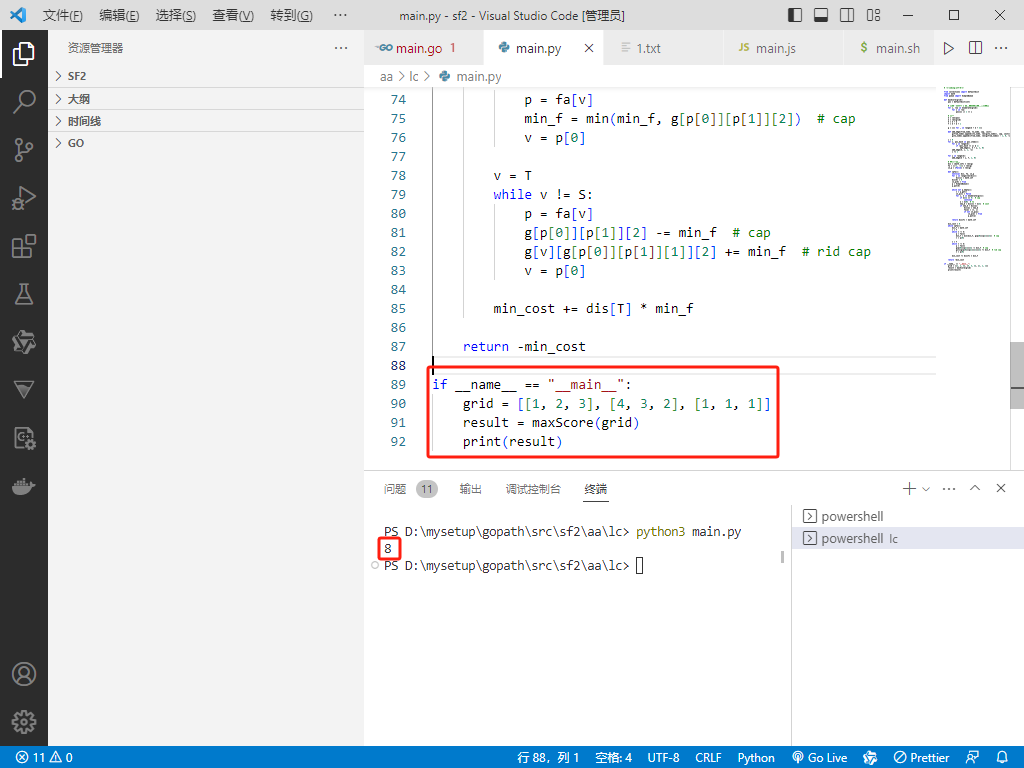
Python完整代码如下：

# -*-coding:utf-8-*-from collections import defaultdictimport mathfrom queue import SimpleQueuedef maxScore(grid): pos = defaultdict(int) # 保存所有包含 x 的行号（压缩成二进制数） for i, row in enumerate(grid): for x in row: pos[x] |= 1 << i # 建图 k = len(pos) m = len(grid) S = k + m T = k + m + 1 g = [[] for _ in range(k + m + 2)] def add_edge(from_node, to_node, cap, cost): g[from_node].append([to_node, len(g[to_node]), cap, cost]) g[to_node].append([from_node, len(g[from_node]) - 1, 0, -cost]) i = 0 for x, pos_mask in pos.items(): for j in range(m): if (pos_mask >> j) & 1: add_edge(i, k + j, 1, 0) add_edge(S, i, 1, -x) i += 1 for j in range(m): add_edge(k + j, T, 1, 0) # 费用流模板 dis = [math.inf] * len(g) fa = [(-1, -1)] * len(g) in_q = [False] * len(g) def spfa(): nonlocal dis, fa, in_q for i in range(len(dis)): dis[i] = math.inf dis[S] = 0 in_q[S] = True q = SimpleQueue() q.put(S) while not q.empty(): v = q.get() in_q[v] = False for i, e in enumerate(g[v]): if e[2] == 0: # cap  continue w = e[0] # to new_d = dis[v] + e[3] # cost if new_d < dis[w]:  dis[w] = new_d  fa[w] = (v, i)  if not in_q[w]: in_q[w] = True q.put(w) return dis[T] < math.inf min_cost = 0 while spfa(): min_f = math.inf v = T while v != S: p = fa[v] min_f = min(min_f, g[p[0]][p[1]][2]) # cap v = p[0] v = T while v != S: p = fa[v] g[p[0]][p[1]][2] -= min_f # cap g[v][g[p[0]][p[1]][1]][2] += min_f # rid cap v = p[0] min_cost += dis[T] * min_f return -min_costif __name__ == \"__main__\": grid = [[1, 2, 3], [4, 3, 2], [1, 1, 1]] result = maxScore(grid) print(result)