【烧脑算法】拓扑排序:从“依赖”到“序列”,理解题目中的先后逻辑
目录
前言
题目
1557. 可以到达所有点的最少点数目
210. 课程表 II
2115. 从给定原材料中找到所有可以做出的菜
2392. 给定条件下构造矩阵
802. 找到最终的安全状态
1591. 奇怪的打印机 II
LCR 114. 火星词典
1203. 项目管理
总结
前言
拓扑排序将一些数据按照一定的先后顺序进行排序。
把拓扑排序想象成一个黑盒,给它一堆杂乱的先修课约束,它会给你一个井井有条的课程学习安排。
这一种在图上的「排序」,可以把杂乱的点排成一排。前提条件是图中无环,从而保证每条边都是从排在前面的点,指向排在后面的点。即对于任意有向边 x→y,x 一定在 y 之前。
拓扑排序实际上类似于BFS,从入度为0的节点一层层的向外进行扩展,知道全部扩完或不能再扩为止。
PS:本篇博客中的所有题目均来自于灵茶山艾府 - 力扣(LeetCode)分享的题单
题目
1557. 可以到达所有点的最少点数目



通过示例一可以转换为:最终返回值是[0,3]
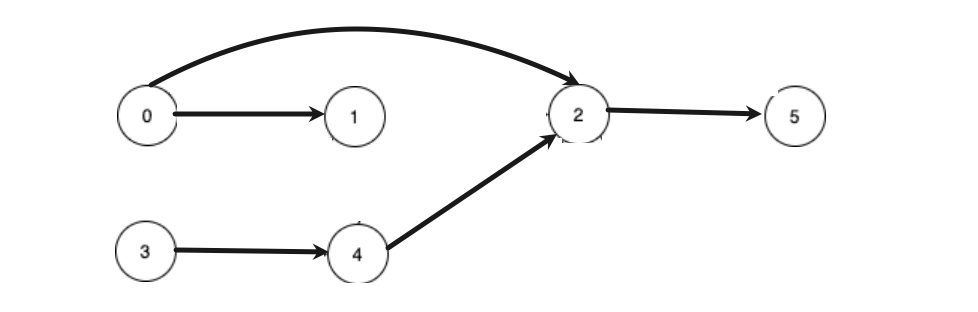
通过图二可以转化为:最终返回值是[0,2,3]。
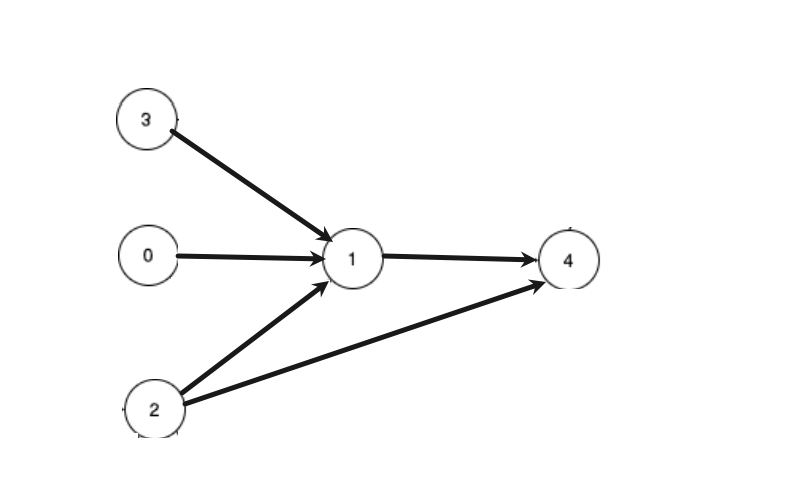
通过以上两个图的展示我们好像发现了一些规律,只要是没有箭头指向的好像就是答案。是不是这样呢???
- 如果y指向x:y->x,那么x必定不属于最小点集,y可能是最小点集,取决于有没有其他点指向y;
- 如果没有数字指向z,那么为了包含所有点,z必须属于最小点集。
综上所述:对于入度为0,即没有点指向的点属于最小点集。
class Solution {public: vector findSmallestSetOfVertices(int n, vector<vector>& edges) { //找出所有 没有数字指向的数 vector ret; unordered_set s; //统计被其他点指向的点 for(auto& tmp:edges) s.insert(tmp[1]); for(int i=0;i<n;i++) if(s.count(i)==0) ret.push_back(i); //如果该点没有被指向就属于最小点集 return ret; }};210. 课程表 II

根据题意可以画一个有向无环图,画示例2:

可以看到我们每次学习都是从最后重要的开始学的,所以可以理解为:
- 对于有其他数字指向的课程,有前置条件不能选择;
- 对于没有数字指向的课程,没有前置条件了,可以选择。
所以可以理解为,对于入度为0的课程可以进行修读,对于入度不为0的课程不能修读。每次选择后该图都会改变,课程的选择是在动态变化的。
class Solution {public: vector findOrder(int numCourses, vector<vector>& nums) { //动态的拓扑排序 vector ret; unordered_set learned; //统计已经学习过的课程 while(ret.size()<numCourses) //每一次循环进行找一次入度为0的课程 { unordered_set s; for(auto& tmp:nums) if(!learned.count(tmp[1])) s.insert(tmp[0]); //有前置条件的课程 if(s.size()==numCourses-ret.size()) return {}; //如果都有前条件,说明学不成了 for(int i=0;i<numCourses;i++) { if(!s.count(i)&&!learned.count(i)) { ret.push_back(i); learned.insert(i); } } } return ret; }};可以通过多次循环找入度为0得到节点,但是使用多次循环必定会造成有多余重复的遍历,明明在学习完一门课程后就可以判断与其相邻的课程时候可以进行学习了,为什么还要重新找一边呢。
所以可以进行优化,可以使用一个队列来实现,让队列中存放入度为0的课程,从队列中选择课程进行学习,学完后判断相邻的课程是否可以进行学习,如果可以就继续入队列。
class Solution {public: vector findOrder(int numCourses, vector<vector>& nums) { //进行优化 vector ret; vector each(numCourses); queue q; //记录可以学习的课程 unordered_map<int,vector> m; for(auto& tmp: nums) { each[tmp[0]]++; m[tmp[1]].push_back(tmp[0]); } for(int i=0;i<numCourses;i++) if(!each[i]) q.push(i); //将可以学习的课程入队列 while(!q.empty()) { int _sz=q.size(); for(int i=0;i<_sz;i++) { int x=q.front(); q.pop(); ret.push_back(x); auto& tmp=m[x]; for(int i=0;i<tmp.size();i++) if(--each[tmp[i]]==0) q.push(tmp[i]); } } if(ret.size()==numCourses) return ret; else return {}; }};2115. 从给定原材料中找到所有可以做出的菜


与上面的拓扑排序类似,只不过此题增加了一个语境:根据已有原料判断可以制作那些菜。可以先将原料可以制作的菜进行存储,在记录每个食物需要的原料个数。通过已有原料将可以通过该原料制作的菜所需的原料数-1,如果原料数将为0就说明可以进行制作了。
class Solution {public: vector findAllRecipes(vector& recipes, vector<vector>& ingredients, vector& supplies) { //依旧是拓扑排序,只不过将数字更改为了字符串,但是原理不变 unordered_map need_dish; //记录每一个菜需要的原料个数 unordered_map<string ,vector> dish_made; //记录每个原料可以做什么菜 int n=recipes.size(); for(int i=0;i<n;i++) //记录每一个原料可以做那些菜,并记录每一个菜需要多少原料 { string& rp=recipes[i]; auto& nums=ingredients[i]; need_dish[rp]=nums.size(); for(auto& str:nums) dish_made[str].push_back(rp); } queue q; for(auto& sp:supplies) if(need_dish.count(sp)==0) q.push(sp); //将不需要其他制作的原料入队列 vector ret; while(!q.empty()) { int sz=q.size(); for(int i=0;i<sz;i++) { auto dish=q.front(); q.pop(); auto& nums=dish_made[dish]; //nums存储该dish可以做那些菜 for(auto& str:nums) { if(--need_dish[str]==0) //将可以制作的菜原料-1,如果所有原料都有了,就可以进行制作了 { ret.push_back(str); q.push(str); } } } } return ret; }};2392. 给定条件下构造矩阵


此题的每个顺序都有优先级顺序,所以需要先确定最下面的才能依次往上确定,确定最右边的才能依次往左确定。
所以可以只用两次拓扑排序,来确定从下往上的顺序,以及从左往右的顺序,随后再将数据进行整合即可;
注意:对于在同一行的数据,我们不需要进行多余的考虑,就算只是同一行的数据我们也对其分上下,因为一共有k行,每个数占一行是肯定够用的。
class Solution {public: vector<vector> buildMatrix(int k, vector<vector>& rowConditions,vector<vector>& colConditions) { // 将行和列分开处理,先确定行的关系,在确定列的关系 vector row; // 数组记录上下顺序,数组从小到大 向上 vector col; // 数组记录左右顺序,数组从小到大 向右 //使用函数记录从下往上和,从右往左的数据 function<void(vector&,vector<vector>&)> turn =[&](vector& dir,vector<vector>& condition) { unordered_map low; // 记录每个数其下面或右边还有几个没有排序的数据 unordered_map<int, vector> up; // 记录每个数下面或右边还有几个数据 for (auto& tmp : condition) { int a = tmp[0], b = tmp[1]; low[a]++; up[b].push_back(a); } queue q; // 记下面没有数字的数 for (int i = 1; i <= k; i++) { if (low.count(i) == 0) { q.push(i); dir.push_back(i); } } while (!q.empty()) { int sz = q.size(); for (int i = 0; i < sz; i++) { int a = q.front(); q.pop(); auto& nums = up[a]; for (auto x : nums){ if (--low[x] == 0) //如果下面的数据都已经排好序了,当前位置也可以进行排序了 { dir.push_back(x); q.push(x); } } } } }; turn(row,rowConditions); //统计从下往上的顺序 turn(col,colConditions); //统计从右往左的顺序 if(row.size()!=k||col.size()!= k) return {}; unordered_map r; //使用两个map确定每个数的横纵做横纵坐标位置 unordered_map l; for(int i=0;i<k;i++) { r[row[i]]=k-1-i; //因为是从下往上的,从右往左的,所以最终结果要反过来 l[col[i]]=k-1-i; } vector<vector> ret(k,vector(k)); for(int i=1;i<=k;i++) ret[r[i]][l[i]]=i; return ret; }};802. 找到最终的安全状态
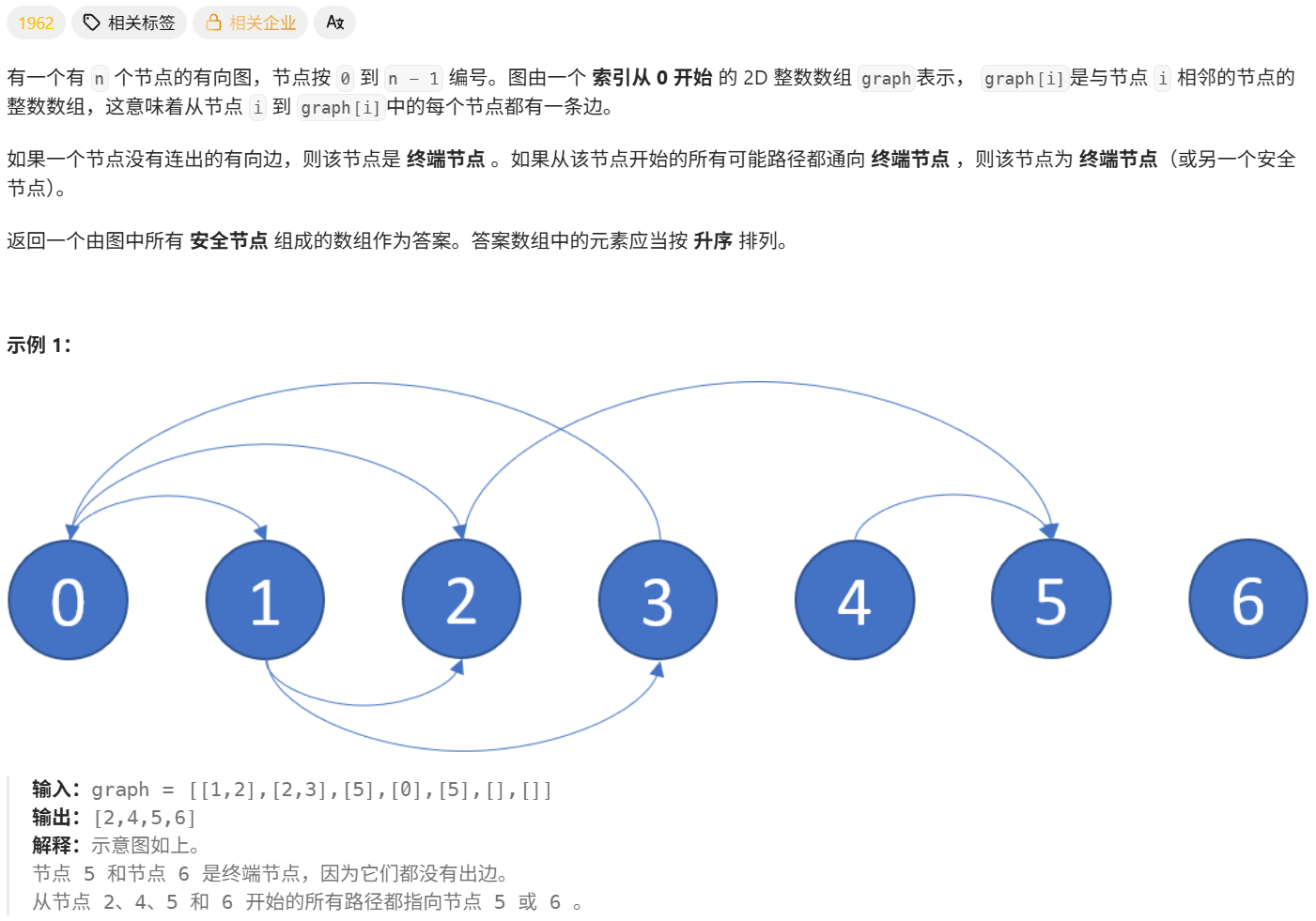
此题依旧是常规的拓扑排序,只不过此题是反过来的,不是从起点位置开始出发,而是从中终点开始找起点。
从终端节点开始出发,看最终能拓展到多少个节点上,当拓展的节点已经每一指向的时候就说明其所有路径都指向终端节点。
class Solution {public: vector eventualSafeNodes(vector<vector>& graph) { //就是所有节点中没有指向的节点以及指向的全是终端节点的节点 int n = graph.size(); unordered_map m; //存放每一个节点指向多少节点 unordered_map<int,vector> each; //记录每个节点被那些节点所指向 for(int i = 0; i < n; i++) { auto& nums = graph[i]; if(nums.size()) m[i] = nums.size(); for(auto& x : nums) each[x].push_back(i); } queue q; //记录没有被指向的节点 for(int i = 0; i < n; i++) if(m.count(i)==0) q.push(i); vector ret; while(q.size()) { int sz = q.size(); for(int k = 0; k<sz ; k++) { int f = q.front(); q.pop(); ret.push_back(f); auto& nums = each[f]; for(auto& x :nums) if(--m[x] == 0) q.push(x); //已经没有指向的节点了,是终端节点 } } sort(ret.begin(),ret.end()); return ret; }};1591. 奇怪的打印机 II

此题有一些难度,算是拓扑排序的应用。
打印机的颜色是一层层的往上添加的,所以我们可以将打印机的颜色一层层的往外取,而在取的时候因为数字是互相关联的,要有顺序的取,该顺序就可以使用拓扑排序,从最上面开始取,依次往下取,看最后时候所有的颜色都取出来了。
如何统计数字的上下层呢???
- 关于数字,先统计数字的上下左右四个边缘;
- 依次遍历矩阵,记录当前数字x,再依次遍历所有数字k,看当前数字是否在其他数字的范围内,如果在则当前数字x覆盖在k的上面,依次进行即可找出所有的覆盖关系;
- 通过覆盖关系,统计每个数字被覆盖的次数;
- 再使用拓扑排序。
具体实现可见以下代码:
class Solution {public: bool isPrintable(vector<vector>& targetGrid) { int n = targetGrid.size(),m=targetGrid[0].size(); int num = 0; for(int i = 0 ;i < n;i++) for(int j = 0 ;j < m;j++) num=max(num,targetGrid[i][j]); //找出矩阵中最大的数 vector col(num+1,true); //用来标记有哪些数字被使用 vector<vector> part(num+1,vector(4,-1)); //0:left 1:up 2:down 3:right for(int i = 0;i < n;i++) { for(int j = 0; j < m ;j++) { int k = targetGrid[i][j]; part[k][0] = part[k][0]==-1?j:min(part[k][0],j); part[k][1] = part[k][1]==-1?i:min(part[k][1],i); part[k][2] = part[k][2]==-1?i:max(part[k][2],i); part[k][3] = part[k][3]==-1?j:max(part[k][3],j); col[k] = false; //对使用过的数字进行标记 } } vector<set> l(num+1); //记录每个数字覆盖了那些数字,此处使用set的目的是为了去重 for(int i = 0;i < n;i++) { for(int j = 0;j < m;j++) { int x = targetGrid[i][j]; for(int k = 1;k <= num ;k++) { if(part[k][0] <= j && part[k][1] = i && part[k][3] >= j && k != x) //x覆盖了k l[x].insert(k); } } } unordered_map count_m; //记录每个数字被覆盖了几次 for(int i = 1;i <= num ;i++) { auto& st = l[i]; for(auto& x: st) count_m[x]++; } queue q; //记录没有被覆盖的数字 for(int i = 1;i <= num;i++) if(count_m.count(i)==0 && col[i]==false) q.push(i); //从最外层开始取,看是否可以取出来 while(!q.empty()) { int sz = q.size(); for(int i = 0; i < sz; i++) { int f = q.front(); q.pop(); col[f]=true; //将颜色去除 auto& st = l[f]; for(auto& x: st) if(--count_m[x]==0) q.push(x); } } return col==vector(num+1,true); //检查是否所有元素都被去除 }};LCR 114. 火星词典


通过将每个字符串进行对比就可以知道所有已知字符的大小关系这样就能构建出图,如果是有向无环图就说明字符的大小关系是合法的,如果出现环就说明不合法。
所以可以使用拓扑排序得到结果:
- 遍历所有的字符串,整理大小关系;
- 统计字符串种出现了那些字符;
- 根据已有字符和字符的大小关系,对字符进行拓扑排序;
- 检查排序后要进行返回的字符串长度是否等于出现的字符个数。
以上是大体思路,但是还有很多细节,可见下面代码实现:
class Solution {public: string alienOrder(vector& words) { //使用拓扑排序,通过将每个字符串进行对比就可以知道所有已知字符的大小关系 //这样就能构建出图,如果是有向无环图就说明字符的大小关系成立,否则不成立 vector<vector> ch; //存储字符之间的关系,其中0下标字符小于1下标字符 int n=words.size(); for(int i=0;i<n;i++) { for(int j=i+1;j<n;j++) { string& s1=words[i]; string& s2=words[j]; int sz1=s1.size(),sz2=s2.size(); int pos1=0,pos2=0; while(pos1<sz1&&pos2<sz2&&s1[pos1]==s2[pos2]) pos1++,pos2++; if(pos2==sz2&&pos1!=sz1) return {}; //如果s2走完了,s1还没走完这种情况是不应该的 if(pos1!=sz1) ch.push_back({s1[pos1],s2[pos2]}); } } //此时所有的比较结果都已经存储起来了 vector m(26); //存储每一个字符前面还有多少比他小的 vector<vector> ln(26); //记录每一个字符后面还有多少比他大的 for(auto& tmp:ch) { m[tmp[1]-\'a\']++; ln[tmp[0]-\'a\'].push_back(tmp[1]-\'a\'); } int count[26],num=0; //记录所有已经出现的字符 for(auto& str:words) for(auto& ch:str) if(++count[ch-\'a\']==1) num++; queue q; //记录前面已经没有比他大的位置 string ret; //记录答案 for(int i=0;i<26;i++) if(m[i]==0&&count[i]) q.push(i); while(!q.empty()) { int sz=q.size(); for(int k=0;k<sz;k++) { int x = q.front(); ret.push_back(\'a\'+x); q.pop(); auto& tmp=ln[x]; for(auto& a:tmp) if(--m[a]==0) q.push(a); } } return num==ret.size()?ret:\"\"; //比较返回的字符串是不是包含全部已经出现的字符 }};1203. 项目管理


对于项目的排列顺序的先后使用一个拓扑排序就行了,但是如何保证每一组的项目相邻呢???
- 如果一个组的谁有项目都可以做了,那就可以让他们所有的项目一起做;
- 但是如果当前项目依赖于其他项目并且该项目不属于向前小组怎么办???此时就需要保证依赖的小组所有项目已经完成了。==那这不又是一个依赖关系嘛,当前小组如果想做项目,其依赖的所有项目的小组都已经做完了所有的工作。==
所以此题需要考虑两个依赖关系:1)项目的依赖关系;2)小组的依赖关系。
步骤:
- 先统计每个项目的前置项目个数,和每个项目后面的具体项目;
- 统计每个小组的前置小组的个数,和每个小组后面的具体小组;
- 对项目进行拓扑排序,看项目能否构成有向无环图;
- 对小组进行拓扑排序,看小组能否个构成有向无环图;
- 如果两个都能构成就说明一定有答案,因为小组的图是根据羡慕的依赖关系制作的;
- 将小组的顺序和项目的顺序进行整合,得到答案。
注意:-1的小组应该如何处理???
此处可以将-1的小组也带上编号,带上额外的其他编号,这些编号的小组没有前置小组所以并不会影响结果。
class Solution { vector topologicalSort(vector& prev,vector<vector>& back,int sz) { vector ret; queue q; //记录可以做的项目或小组 for(int i=0;i<sz;i++) if(!prev[i]) q.push(i); while(q.size()) { int n=q.size(); for(int i=0;i<n;i++) { int x=q.front(); q.pop(); ret.push_back(x); for(auto& a:back[x]) if(--prev[a]==0) q.push(a); } } return ret.size()==sz?ret:vector(); }public: vector sortItems(int n, int m, vector& group, vector<vector>& beforeItems) { for(auto&x: group) if(x==-1) x=m++; //将-1的小组带上编号 vector prev_grp(m); //记录每个小组前置的小组个数 vector<vector> back_grp(m); //记录每个小组后面的小组 vector prev_item(n); //记录每个项目的前置项目 vector<vector> back_item(n); //记录每个项目后面的项目 for(int i=0;i<n;i++) { int g=group[i]; //所属组 auto& nums=beforeItems[i]; //前置项目 prev_item[i]=nums.size(); //前置项目的个数 if(nums.size()) { set s; for(auto& obj:nums) { back_item[obj].push_back(i); //i项目在ojb项目的后面 int prev=group[obj]; //前置项目的所属组 if(!s.count(prev)&&prev!=g) { prev_grp[g]++; back_grp[prev].push_back(g); } s.insert(prev); } } } vector grp=topologicalSort(prev_grp,back_grp,m); vector itm=topologicalSort(prev_item,back_item,n); if(grp.empty()||itm.empty()) return {}; vector ans; //将小组中项目的先后顺序进行整合 vector<vector> each_obj(m); for(auto& it:itm) each_obj[group[it]].push_back(it); for(auto& g:grp) ans.insert(ans.end(),each_obj[g].begin(),each_obj[g].end()); return ans; }};总结
对于拓扑排序类型的题目处理来做也不是很复杂,也有一定的套路:
- 先根据已有信息,将每个数的关系记录下来,包括前面数据的个数,以及后面具体的数据;
- 从入度为0的开始依次向外进行扩展。
- 检查最终的答案是否与预期结果一样。
对于有些比较难的拓扑排序题目,可能不止存在一个关系,可能存在多个关系,比如最后一题,此时就需要对每个关系进行分类,整合。


