贪心算法的 “反直觉” 时刻(一):重新认识局部最优



专栏:算法的魔法世界
个人主页:手握风云
目录
一、贪心算法简介
二、例题讲解
2.1. 柠檬水找零
2.2. 将数组和减半的最少操作次数
2.3. 最大数
2.4. 摆动序列
一、贪心算法简介
贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。它是一种解决优化问题的方法。贪心算法的核心思想是“活在当下,只顾眼前”。它在每一步都做出局部最优的选择,并期望这些局部最优选择能够最终导向全局最优解。
贪心算法的核心就是对于贪心策略的提出:1. 把解决问题的过程分为若干步;2. 解决每一步的时候,都选择当前看起来最优的解法;3. 希望得到全局最优解。
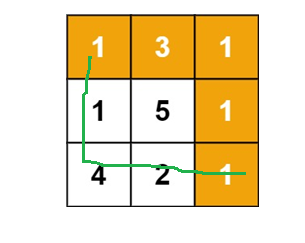
贪心算法的可以应用于找零问题,比如拿50块钱去买4块钱的东西,商家需要找46块钱,我们希望找回的纸币的张数最少,我们可以先用两张20的来凑40块钱,再用5块和1块来凑剩下的6块。第二个场景是最短路径,在力扣的第64题最小路径和中,我们按照贪心的思路来,局部最优,3>1先向下走一步,5>4再向下走一步,接下来只能向右走到达终点,路径和为9。第三个场景,完全背包问题,我们可以根据体积提出贪心策略,就往背包里装体积最小的物品,也可以根据最大价值提出贪心策略,一开始就往背包里面装最大价值的物品,甚至可以根据体积与价值之比提出贪心策略。
贪心算法的难点:1. 贪心算法不同于双指针、二分、模拟、分治等可以举一反三的算法,因为每一道题的贪心策略没有一个标准,导致提出的贪心策略不同;2. 贪心策略的正确性证明,因为贪心算法会因为一时的贪婪和短浅的目光,只能得到一个局部最优解,但并非是全局最优解。
对于贪心算法的证明,我们可以用到数学中任意见到的证明方法。
二、例题讲解
2.1. 柠檬水找零

这道题的要求是模拟一个柠檬水摊的找零过程。每一杯柠檬水的售价为5美元,顾客会按顺序给你5美元、10美元或20美元。你需要给每个顾客正确找零,也就是说净交易是每位顾客向你支付5美元。一开始你手头没有任何零钱。
我们需要先分情况讨论,顾客可以给我们5、10、20美元的钞票。如果是5美元,直接收下;如果是10美元,则找给顾客5美元,当然前提是自己手头上有5美元;如果是20美元时,则可以分为可以找一张10美元和一张5美元,或者是三张5美元,所以如何保留手头上的5美元成了关键。如果手拿20美元的顾客后面有一个手拿10美元的顾客,如果我们优先把5美元找给前一位,会导致后面无法正常找零,所以贪心策略就是手头上有10美元,优先找给手拿20美元的顾客。
完整代码实现:
class Solution { public boolean lemonadeChange(int[] bills) { // 定义5美元和10美元的数量 int five = 0, ten = 0; for (int i : bills) { if (i == 5) { five++; } else if (i == 10) { if (five == 0) { return false; } five--; ten++; } else { if (five != 0 && ten != 0) { five--; ten--; } else if (five >= 3) { five -= 3; } else { return false; } } } return true; }}贪心策略的证明:本题用到的是交换论证法,在不破环最优解的最有性质的前提下,能够将最优解调整为贪心解。5美元的账单不用找零,10美元的账单只能找5美元,贪心的关键在于20美元账单的找零。第一种情况,在最优解后面的账单中,压根没有用到10美元的找零,那我们就可以提前使用10美元执行贪心策略;另一种情况最优解的后面用到贪心解里的10美元,此时依旧不会受到影响,能够正确找零。
2.2. 将数组和减半的最少操作次数

题目要求给定一个正整数数组nums,通过选择数组中的任意一个数并将其减小到恰好一半的操作,使得数组和至少减少一半的最少操作次数。每次操作后,可以继续对减半过的数进行操作。需要返回的最少操作次数使得数组和至少减少一半。
贪心策略就是每次找出数组中的最大元素进行减半,但如果去遍历数组找到最大值,时间复杂度会非常恐怖,所以我们可以借助大根堆来实现。
完整代码实现:
class Solution { public int halveArray(int[] nums) { // 创建一个最大堆 PriorityQueue heap = new PriorityQueue((a, b) -> b.compareTo(a)); double sum = 0.0; for (int i : nums) { heap.offer((double) i); sum += i; } sum /= 2; // 初始化计数器 int count = 0; while (sum > 0) { // 从堆中取出最大的元素,并将其除以2 double t = heap.poll() / 2.0; // 将数组的总和减去除以2后的元素 sum -= t; count++; heap.offer(t); } return count; }}贪心策略的证明:本题用到的依然是交换论证法。从左向右依次扫描我们减半的数字,当第一次遇到不一样的数字时,因为贪心解始终是挑最大的数,所以x一定大于y。如果x在最优解中没有用到,如果我们用x替换了y,那么x一定也可以让数组最小和减半;如果x在最优解中使用过,我们把x减半的时机提前了,此时交换x和y减半的操作依然不影响最小操作数。
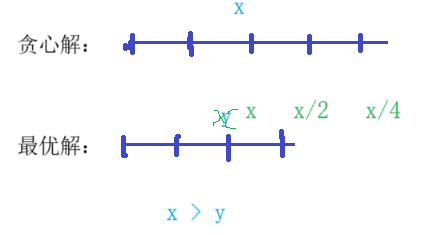
2.3. 最大数

这道题目要求我们给定一组非负整数,重新排列每个数的顺序,使其组成一个最大的整数。需要注意的是,输出结果可能非常大,所以我们需要返回一个字符串而不是整数。
本题的算法原理与排序算法及其类似。排序的本质,就是确定元素的先后顺序。我们之前学到的排序算法,如果我们要想让数据成升序排列,如果a>b,那么a在前,b在后,a=b,顺序无所谓,如果ab且b>c,那么我们可以推出a>c)。这是我们特别容易忽略的一点,ab>ba,bc>cb,我们可以推出a在b的前面,b在c的前面,而我们如何推出a在c的前面呢。
完整代码实现:
class Solution { public String largestNumber(int[] nums) { int n = nums.length; String[] strs = new String[n]; // 将数字转换为字符串并存储到字符串数组中 for (int i = 0; i { return (b + a).compareTo(a + b); }); StringBuffer ret = new StringBuffer(); for (String s : strs) { ret.append(s); } // 如果排序后的第一个字符为\'0\',则说明所有数字都为0 if (ret.charAt(0) == \'0\') { return \"0\"; } return ret.toString(); }}证明贪心策略的正确性,需要用到离散数学里的全序关系中的全序性、反对称性与传递性。先证明全序性:假设a有x为,b有y位,那么ab就可以表示为10^y*a+b,ba可以表示为10^x*b+a,通过上面两个元素可以进行比较,具有全序性。证明反对称性:可以根据“夹逼定理”推断出ab>=ba且ba>=ab,则ab=ba。证明传递性:这里需要注意要把0当作1位数,我们依然可以按照上面的思路推导出传递性。
2.4. 摆动序列

给定一个整数数组,找到最长的连续子序列,使得序列中相邻元素的差值交替正负。例如,对于数组 nums = [1,7,4,9,2,5],其中一种摆动子序列是 [1,7,4,9,2,5],因为差值序列为[6,-3,5,-7,3],交替为正负。
我们这里用折线图的形式来表示数组元素的变化情况。当我们把折线图画出来之后,就可以从宏观角度找出极值点。我们贪心的策略就是尽可能地找出更多的点来形成摆动序列,如果我们跳过这些波峰和波谷的,那么得到的子序列长度一定不是最长的。贪心策略就是统计出波峰以及波谷的数量。
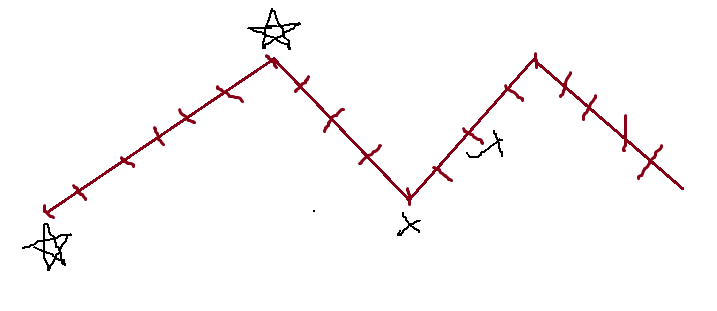
接下来的难点就是如何统计个数。如果是波峰,那我们就看这个元素的与左侧之差为正,与右侧之差为负;如果是波谷,那我们就看这个元素的与左侧之差为负,与右侧之差为正。但还有一个比较麻烦的点:如果相邻元素是相同的,左边这两种情况就不存在波峰与波谷,但右边这两种情况存在波峰和波谷。我们可以使用全局变量left来忽略掉中间相同的元素,只考虑最左侧和左右侧的元素。如果left=0,则可增可降;left0,表示单调递增。
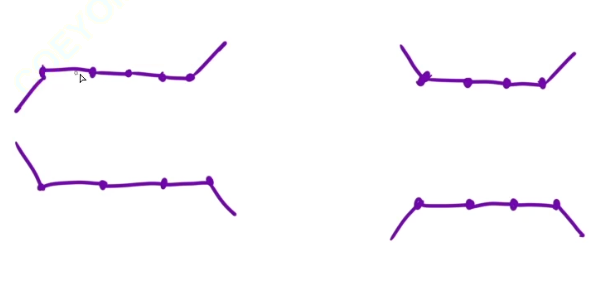
完整代码实现:
class Solution { public int wiggleMaxLength(int[] nums) { int n = nums.length; // 如果数组长度小于2,直接返回数组长度 if (n < 2) { return n; } // 初始化结果为0,左值为0 int ret = 0, left = 0; for (int i = 0; i < n - 1; i++) { int right = nums[i + 1] - nums[i]; // 如果差值为0,跳过 if (right == 0) { continue; } // 如果左值乘以差值小于等于0,结果加1 if (left * right <= 0) { ret++; } // 更新左值为差值 left = right; } return ret + 1; }}

