数据结构 --- 堆

堆 --- Heap

• 前言
• 一、整体结构
• 二、相关方法
• • 1.初始化
  • 2.销毁
  • 3.入堆
  • 4.向上调整算法
  • 5.出堆
  • 6.向下调整算法
  • 7.打印
  • 8.判空
  • 9.取堆顶元素
  • 10.获取堆元素个数
• 三、堆排序
• • 1.思想及代码
  • 2.时间复杂度

前言

堆是一种特殊的数据结构，是一个底层用数组实现的完全二叉树。堆有两种分类：大堆（也叫大根堆）和小堆（也叫小根堆），大堆就是双亲节点的大小要大于其左右孩子节点，小堆就是双亲节点的大小要小于其左右孩子节点，例如下图：

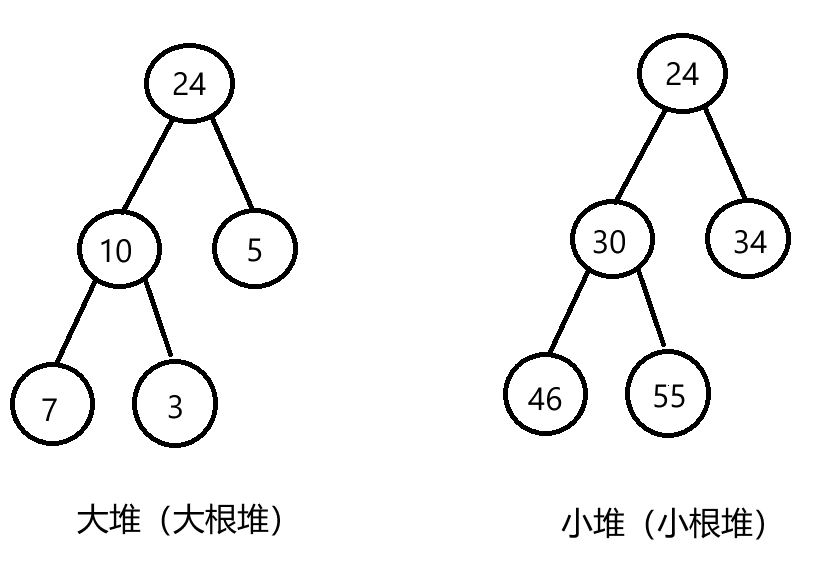
本此实现使用C语言实现。

一、整体结构

本次实现堆结构底层采用数组的形式，共有三个属性，指向数组的指针arr，实际元素个数size和空间容量capacity。

// 堆的结构typedef int HPDataType;typedef struct Heap{HPDataType* arr; // 指向数组的指针int size;  // 实际元素个数int capacity; // 空间容量}Hp;

二、相关方法

1.初始化

堆的初始化方法就是将其数组置为NULL，size和capacity置为0。

// 初始化void HPInit(Hp* php){php->arr = NULL;php->size = php->capacity = 0;}

监视窗口观察：

这里的hp是实参，代码中php是形参。

2.销毁

堆的销毁就是将数组中动态开辟的空间释放掉，之后置为NULL，之后再将size和capacity恢复为0。

// 销毁void HPDestroy(Hp* php){// 堆非空才销毁，为空没必要销毁if (php->arr){// 堆的空间都是动态开辟出来的free(php->arr);php->arr = NULL;}php->size = php->capacity = 0;}

3.入堆

入堆操作是在堆尾进行的，并且操作进行结束后，堆整体的结构不能改变，即不能改变小堆或者大堆的结构，所以最后会进行数据的调整，此时就要使用向上/向下调整算法了。
入堆整体三个要点：
1）首先判断是否需要扩容
扩容操作就是当堆的size等于capacity时，这种情况需要扩容，使用realloc进行2倍扩容，当最开始向空堆插入数据时，capacity等于0，此时将其设定初始值，最后扩容完成后需更新数组的指向（动态开辟的空间是临时空间）和容量大小。
2）堆尾入数据
堆尾就是刚好size处的位置，再此位置插入数据即可。
3）调整堆中的数据，以满足整体堆结构
调整数据是向上调整算法，因为插入的数据是在树的底部，所以是向上调整。详细解释请看第4小点。

// 入堆 --- 堆尾入数据void HPPush(Hp* php, HPDataType x){assert(php);// 首先判断是否需要扩容if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* temp = (HPDataType*)realloc(php->arr, sizeof(HPDataType) * newcapacity);if (temp == NULL){perror(\"realloc!!!\");exit(1);}php->arr = temp;php->capacity = newcapacity;}// 数据入堆php->arr[php->size] = x;// 确保入堆数据后依旧是大堆/小堆，需要向上调整数据AdJustUp(php->arr, php->size);php->size++;}

演示向一个空堆push7个数据：

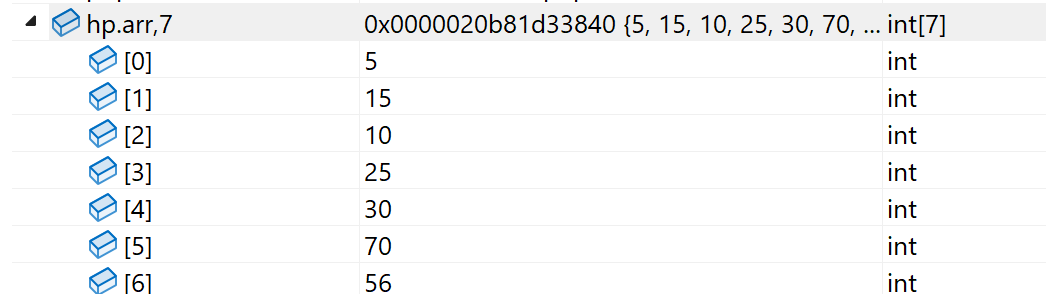
最终此堆成为的是一个小堆结构，因为入堆代码里面的向上调整算法设定的是小堆。

最后别忘记了加加size。
时间复杂度：
只有AdJustUp方法内有循环，并且child的走向只由树的深度决定，还有在一颗深度为h的二叉树中，节点总个数n = 2^h - 1，所以深度h = log以2为底n+1的对数，所以入堆的时间复杂度O(n) = logn。

4.向上调整算法

由二叉树的性质可有：假设孩子节点（child）的标号为i，则双亲节点（parent）的标号为(i-1) / 2。知晓这条性质即可写出向上调整算法。
图解：

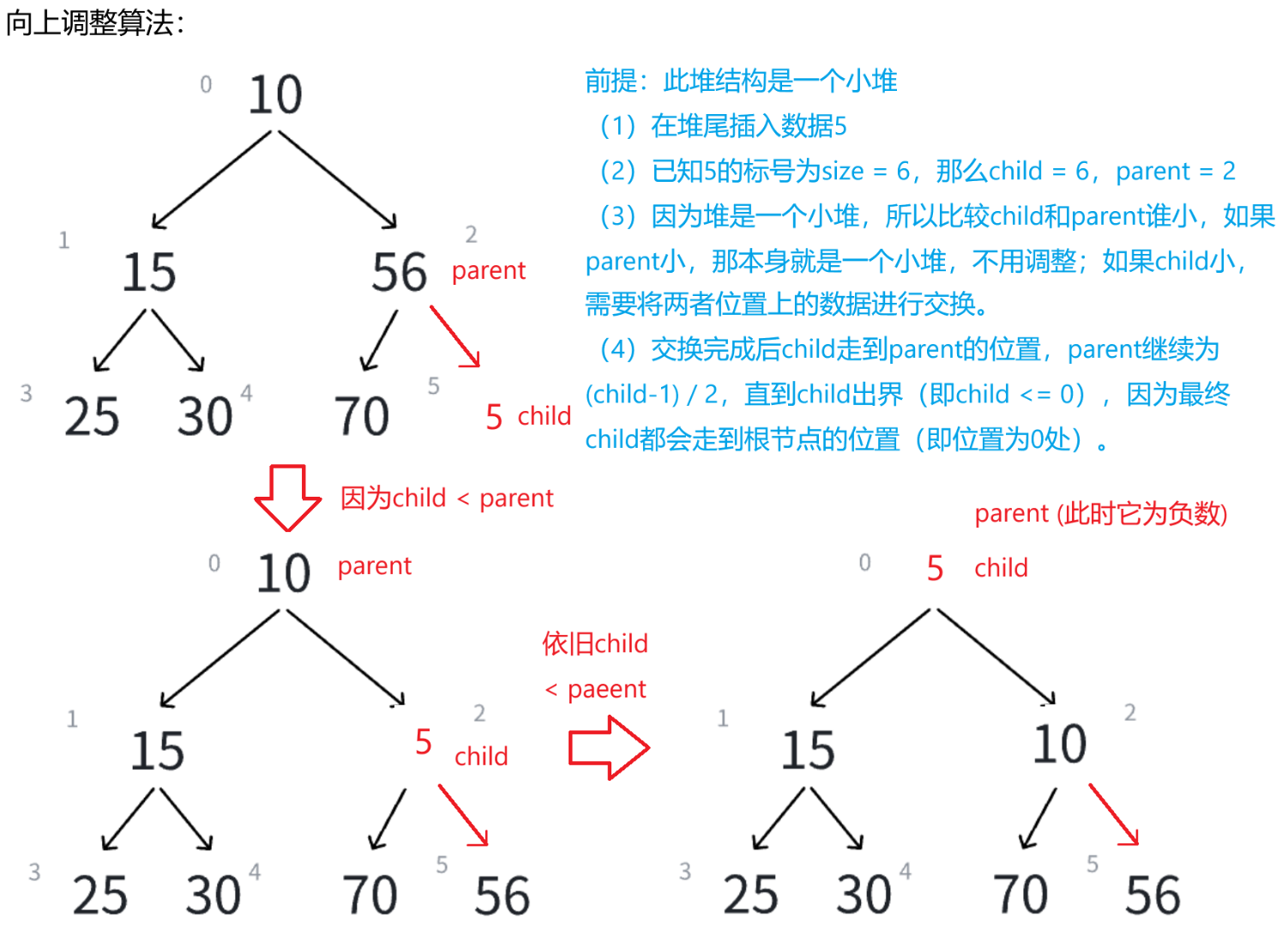
// 向上调整算法void AdJustUp(HPDataType* arr, int child){// 父（双亲）节点的标号int parent = (child - 1) / 2;// 小堆：<// 大堆：>while (child > 0){if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}

5.出堆

对于堆这种结构，是在堆顶出数据，只不过底层是数组的情况下，堆顶出数据效率很低，所以这里就先将堆顶和堆尾的数据交换，底层数组的情况下，尾部出数据效率很高，所以这里先交换，再将size减减，即出掉堆顶数据，最后再将剩余元素调整回堆结构即可，此时调整算法使用的是向下调整算法。

// 出堆 --- 堆顶出数据void HPPop(Hp* php){assert(!HPEmpty(php));// 为了不破坏堆的整体结构，先将堆顶和堆尾的数据交换Swap(&php->arr[0], &php->arr[php->size - 1]);// 再将size减减，出掉堆顶数据--php->size;// 同样确保交换堆顶数据和堆尾数据后依旧是大堆/小堆，需要向下调整数据AdJustDown(php->arr, 0, php->size);}

演示：

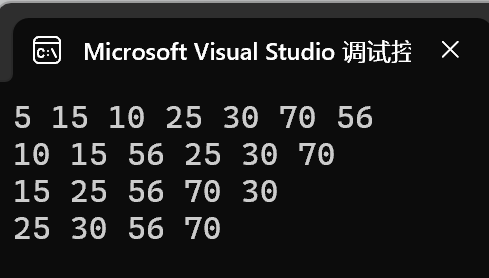
将堆顶元素出掉后，剩余元素回调整，恢复成大堆或者小堆结构。

6.向下调整算法

这里的向下调整算法是知晓根节点的标号，获得左右孩子的标号，再进行比较和交换，使其成为一个堆结构。
由二叉树的性质可知，假设双亲节点（parent）的标号为i，则左孩子节点（child）的标号为 i * 2 + 1，右孩子节点的标号就为child+1。根据此性质即可推出向下调整算法。
图解：

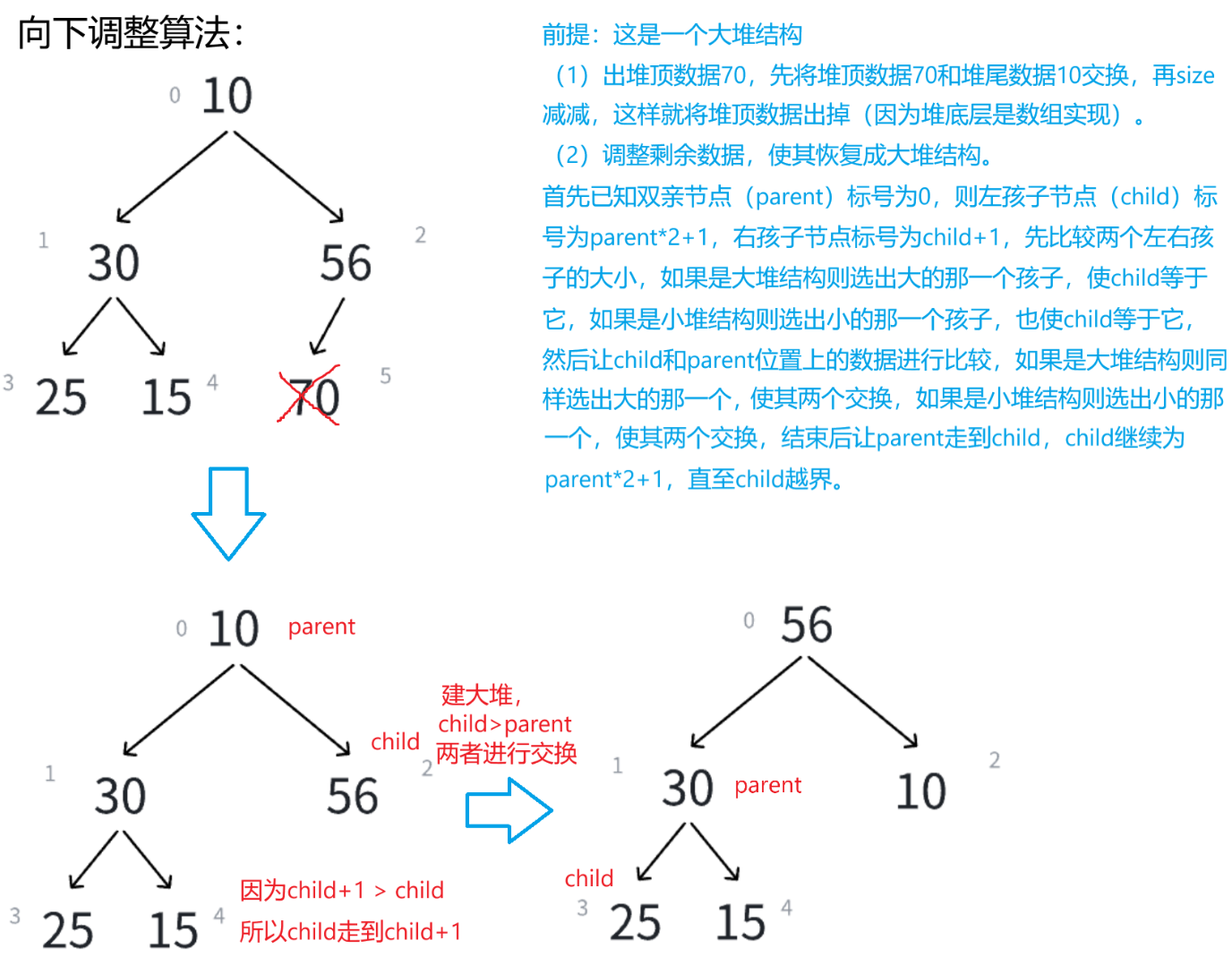
// 向下调整算法// parent是根节点的标号，n是堆的元素个数void AdJustDown(HPDataType* arr,int parent,int n){// 左孩子节点的标号// 右孩子节点的标号 = 左孩子节点的标号 + 1int child = parent * 2 + 1; // 左孩子while (child < n){// 这里要确保有右孩子，没有右孩子则child+1会越界// 大堆：<// 小堆：>if (child + 1 < n && arr[child] < arr[child + 1]){child++;}// 大堆：>// 小堆：<if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}

7.打印

打印即将底层数组的元素一一打印出来。

// 打印void HPPrint(Hp* php){for (int i = 0; i < php->size; i++){printf(\"%d \", php->arr[i]);}printf(\"\\n\");}

8.判空

判空即是堆中是否有数据，看size属性是否为0。

// 判空bool HPEmpty(Hp* php){assert(php);return php->size == 0;}

9.取堆顶元素

取堆顶元素也就是取出数组第一个元素，即下标为0的元素。

// 取堆顶元素HPDataType HPTop(Hp* php){assert(!HPEmpty(php));return php->arr[0];}

10.获取堆元素个数

由于堆结构本身就有size属性，直接返回size即可。

// 获取堆元素个数int HPsize(Hp* php){assert(php);return php->size;}

三、堆排序

1.思想及代码

这里的堆排序只是借助堆的思想，而不是借助堆这一个结构。
相当于对数组进行改造，改造成为堆，再进行排序。
有三个要点：
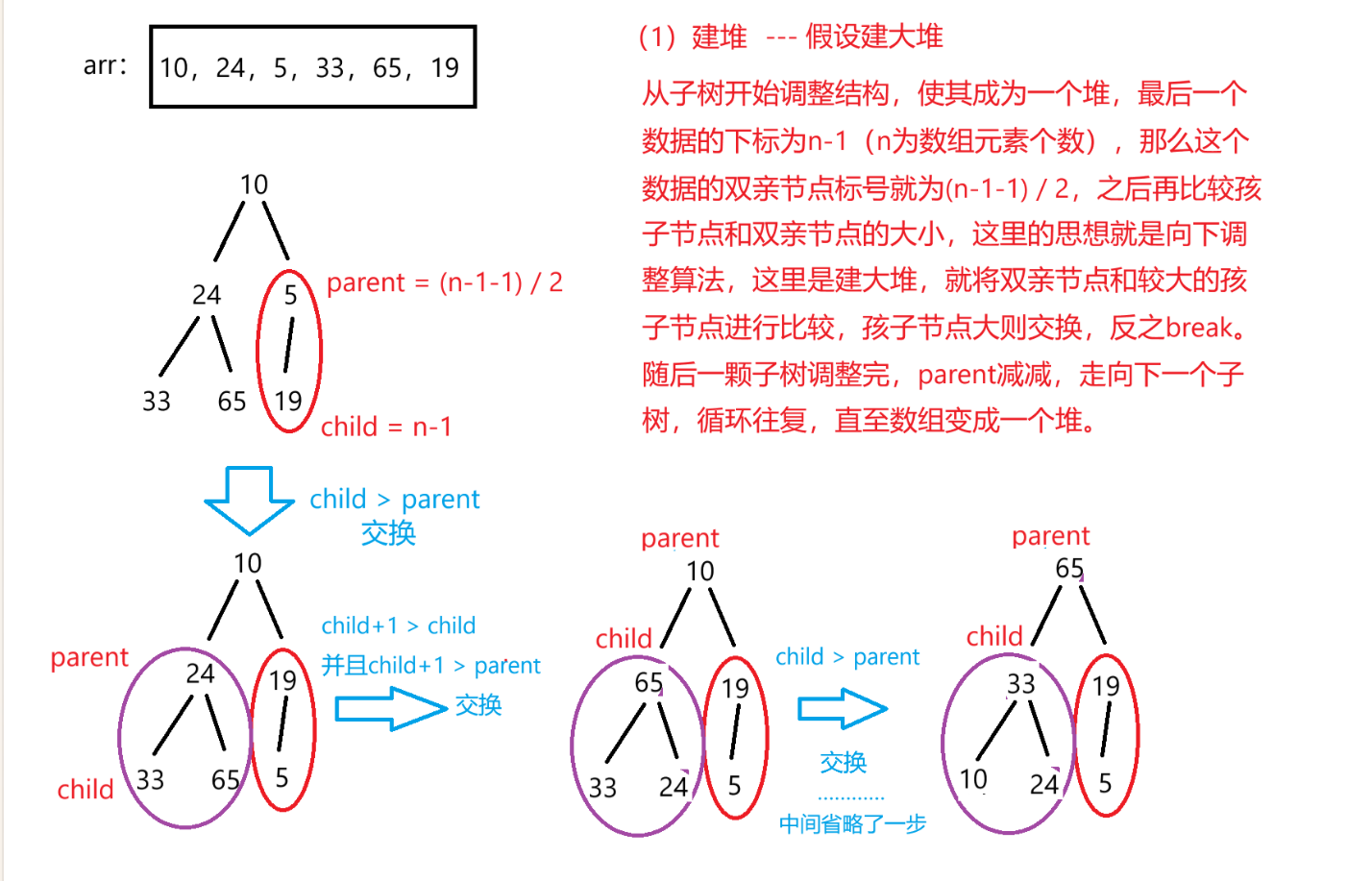
1）先将数组建成一个堆结构。
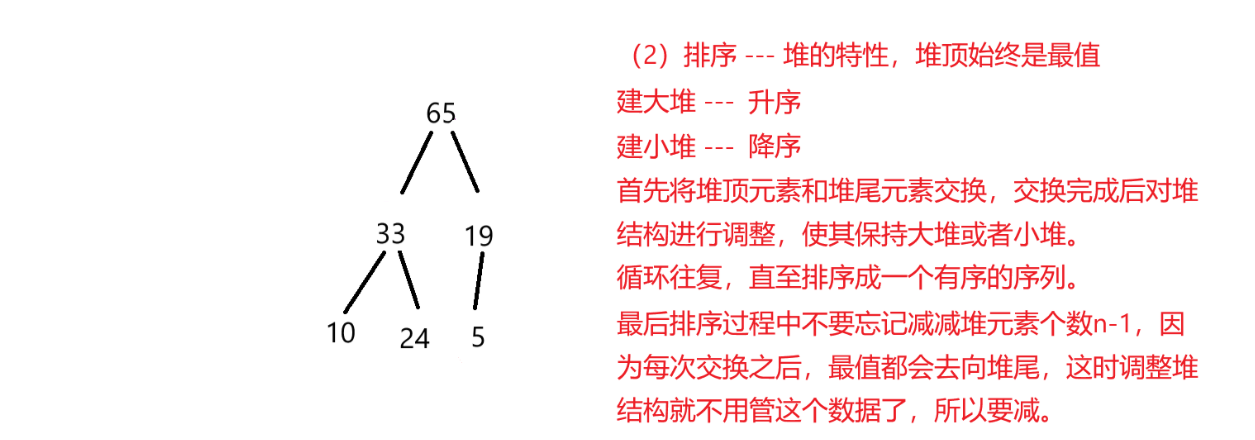
2）排序之前优先将堆顶和堆尾的数据进行交换，此时堆尾就是存储着堆的最值，此时就不用管他了，直接将其有效元素个数减1，再将剩下的数据恢复为堆结构，如此循环往复，直至数组成为有序的序列。
3）建大堆 - - - 排完序后是升序序列，建小堆 - - - 排完序后是降序序列。

向下调整建堆图解：


向上调整建堆图解：

// 堆排序// 借助堆的思想，而不是借助堆的结构void HPSort(int* arr, int n){// 建堆 --- 将arr数组改造成堆// 向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdJustDown(arr, i, n);}// 向上调整建堆for (int i = 0; i < n; i++){AdJustUp(arr, i);}// 堆排序// 先将堆顶和堆尾数据进行交换，int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdJustDown(arr, 0, end);end--;}}

演示：
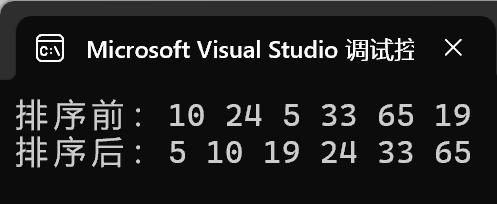
建成大堆，排序后是升序序列。

建成小堆，排序后是降序序列。

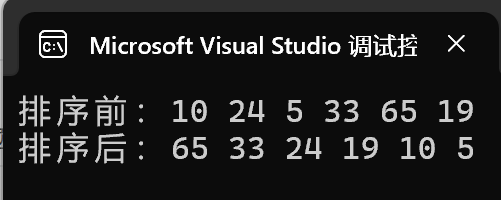
2.时间复杂度

堆是一颗完全二叉树，这里为了更加方便的探究时间复杂度，使用满二叉树进行研究（满二叉树也是完全二叉树），时间复杂度本身也是一种估计求值，多一些节点少一些节点都无关紧要。
1）向下调整建队时间复杂度：

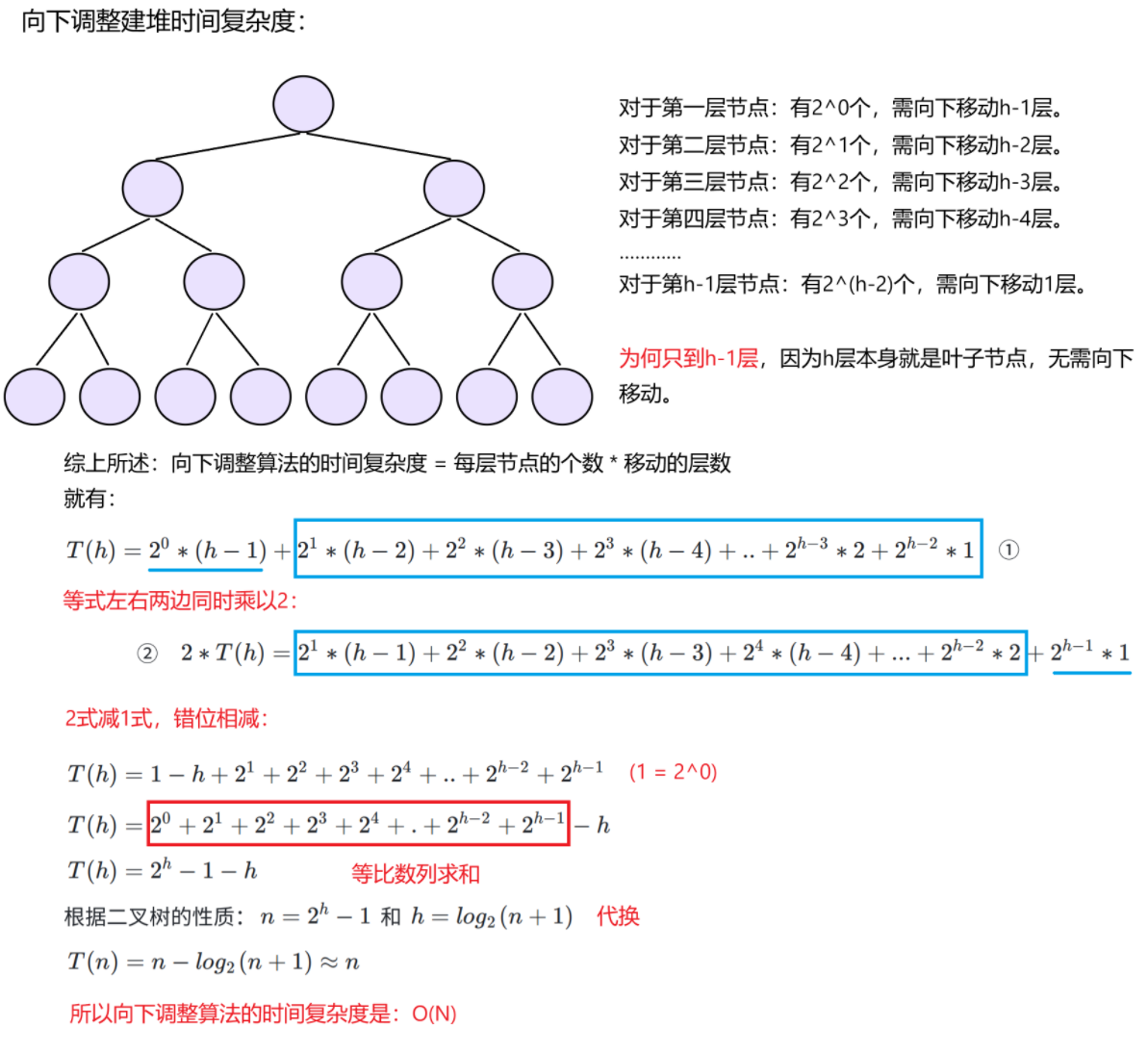
总结：对于向下调整建堆，由于是向下调整数据，越往下调整虽然节点变多但是调整的层数变少。

2）向上调整建队时间复杂度：

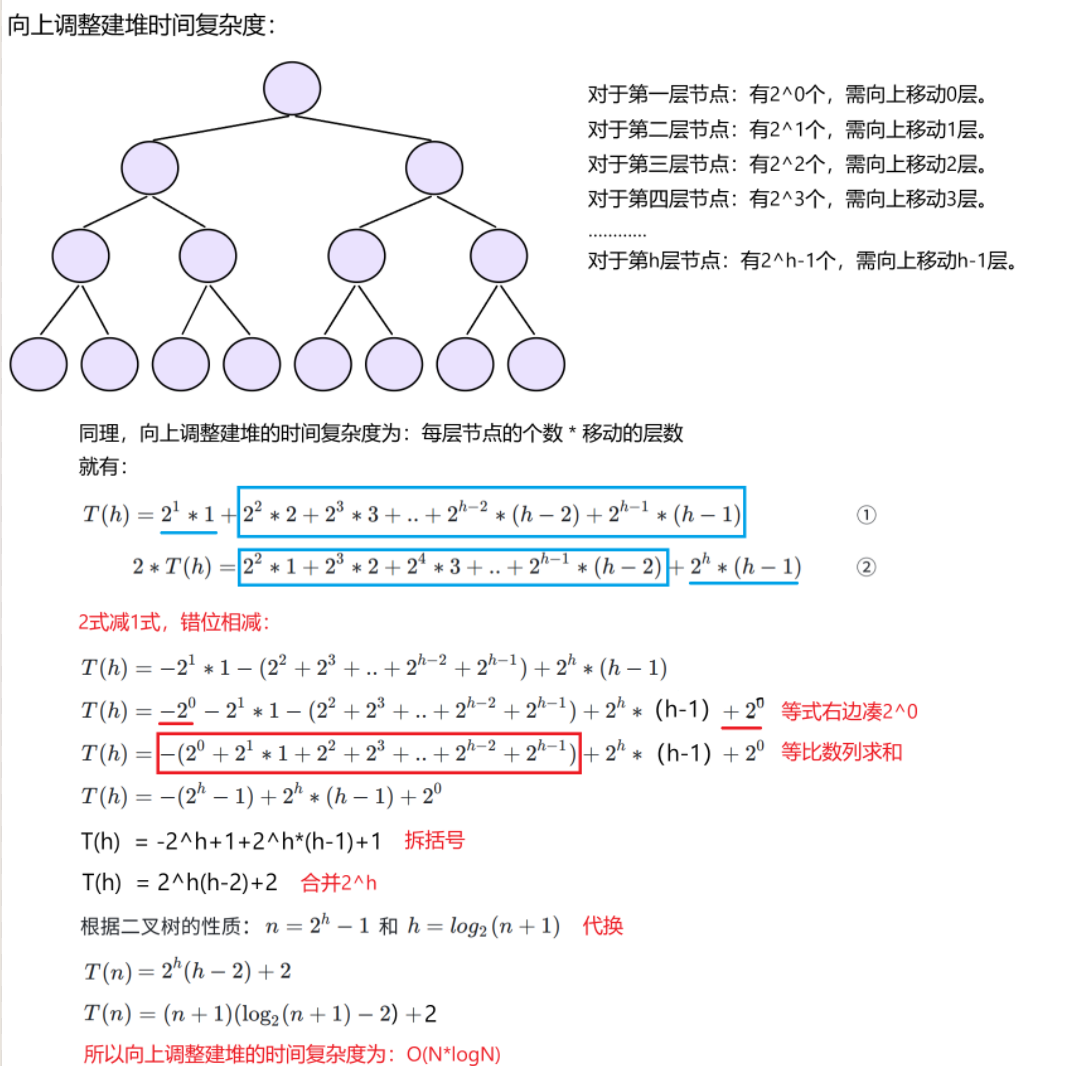
总结：对于向上调整建堆，由于是向上调整数据，越往上调整虽然节点变少，调整的层数也变少，但是其决定性作用下层节点既多，调整的层数也多。

所以结合上述两次总结向下调整建堆的时间复杂度要优于向上调整建堆的时间复杂度。

3）堆排序的时间复杂度
综上，取最坏时间复杂度(NlogN)，结合向下调整算法的时间复杂度(logN)，所以堆排序的时间复杂度即为O(NlogN)。