阳光算法:一种比RRT*更快的平面移动机器人复杂场景下路径规划算法
本方法由燕山大学机械国重教师邓英杰、徐艺菲共同提出,构建了一种全新的基于采样的平面路径规划算法,其工作原理完全不同于现有RRT系列算法,更加适合解决迷宫等复杂地形下的全局路径规划问题。该算法非常简捷,效率较高,其计算复杂度经证明比RRT*更低。目前,该算法已发表在如下期刊,且源代码已开源。
Y. Deng and Y. Xu, Sunlight Algorithm: A Novel Shortest Path Planning Technique for Unmanned Surface Vehicles With Enhanced Search Efficiency, IEEE Transactions on Intelligent Transportation Systems, 2025,doi: 10.1109/TITS.2025.3590007.
传统路径规划算法包括:基于网格的算法和基于采样的算法两大类。基于网格的算法,如A*、Dijkstra、快速行进算法等均需要依托地图网格进行路径寻优,算法精度受到网格精度的影响。基于采样的算法,以RRT及其变体为代表,具有不需要环境建模,计算速度快的优点。RRT*算法作为RRT的里程碑式改进,被证明具有渐近最优性,目前已经被广泛应用在各个路径规划领域。在RRT*基础上的改进,如Q-RRT*、F-RRT*等也被认为是具有重要学术意义的研究。然而,作者在进行RRT*算法应用时,发现:RRT*在复杂场景下的路径搜索效率很低,通常需要迭代上万次才能找到最优路径,且当采样点数目过多时,RRT*的Rewire机制会严重制约算法的速度。
那么,有没有一种在复杂环境下,又快又好的路径规划算法呢?现在很多关于路径规划的研究侧重于将多种新颖的方法结合,或者将深度强化学习技术引入,已经很少有人关注基础但又实用的路径规划算法研究了。作者在观看完电影《普罗米修斯》后,对其中无人机洞穴地形扫描的科幻场景印象深刻,其中,无数个小无人机通过不断对洞穴中的各个方向探测扫描,逐步建立起整个洞穴的地图信息。如果我们把无人机作为光子,从起点发射无数个光子,每个光子照射到边界后,在该位置重新发射无数个光子,不断重复该过程,那么绝对也能从起点找到一条到终点的最短路径,无论该环境有多复杂。该思路模拟阳光的照射行为,于是将其起名为:阳光算法。如果我们在每个点发射无数条光线,那么光子采样到的点也有无数个,计算量也太大了,根本不合理。在算法运行中,其实并不需要无数条光线,假设0-360度范围内,每间隔1度发射1条光线,采样效果也很好,如图1左侧所示。另外,并不是每个被照射的点都有意义,最短的路径永远出现在拐角处,我们只需要采集地形或障碍边缘的切点就好了,如图1右侧所示。
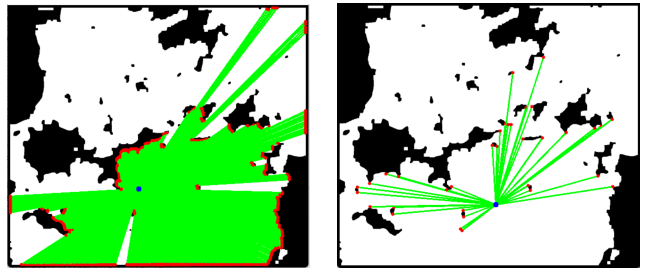
图1 左图为360度照射采样,右图为切点采样(蓝色点是太阳,红色点是采样点)
好了,了解了基本原理,下面开始讲作者发明的这个算法,这个算法非常简单,包括3段主要代码,又简单又实用,只要高中的数学知识就够了。还记得上一段讲的那个切点吗?这个切点的采样是有讲究的,作者通过判断相邻两根光线的长度差来判断是否存在切点。如果长度差超过一个阈值,则说明切点存在,切点位置的选择方法为:在相邻两根光线中长度较长那根光线的方向上,拓展一个长度较短那根光线的长度+1个前向距离的长度。如图2所示。
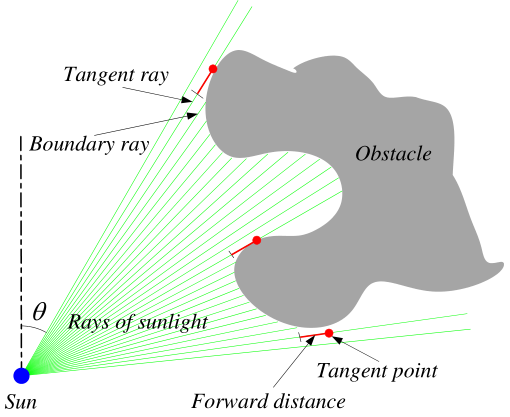
图2 切点的采样方法
可能有人会问,为啥还要引入一个前向距离呢,直接采样切点就行了啊?其实,其作用在于拟合障碍物边界并避免被困住。例如,对于如图3所示的曲线障碍边界,如果没有前向距离,切点会被困住,阳光不会前进,引入了前向距离后,就能通过障碍边界并照射到终点了。
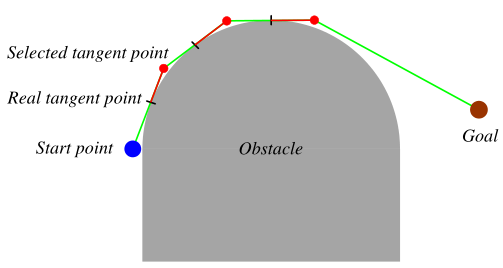
图3 前向距离的作用
切点采样的伪代码如Algorithm 2所示,原理和上面讲的一样,就是判断是否存在切点的阈值,
就是前向距离,
是采样的长度步长,
是阳光照射角度的步长。
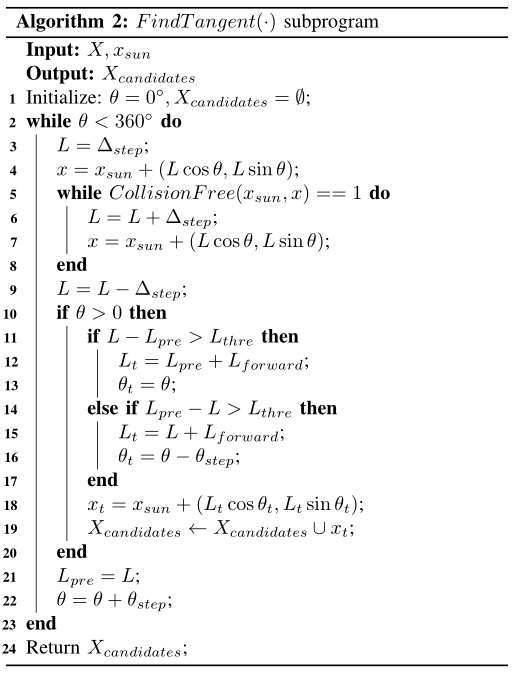
然后,介绍主程序代码,如Algorithm 1所示。首先,设置一个开集Openset用于存放上面的切点,该开集最初只存储了起点,其他的变量不重要,边和顶点的定义和大多数论文是一样的。当开集不为空,或者迭代次数少于最大次数就一直运行(这块根据需要调整,比如:当路径长度不再减少了就停止程序等)。通过ChooseSun函数从开集里取出一个点作为太阳
,这个选取太阳的方法,我们在论文里用了和A*算法一样的启发式搜索策略,当然,只按照广度优先原则选取也可以,即优先考虑经由光线路径到达起点的距离最近的点。每选取一个
后,将该点从Openset中移除。判断
是否可以直接照射到终点
,若可以,则发现新路径,并将该路径放入搜索到的路径集Pathset。接下来,通过上段的FindTangent函数找到
的所有切点,并放入
集合中,引入本方法中的两个重要机制对集合中的点进行筛选,即NotBrother和NotOtherSon机制。Brother的意思是:
的切点同时也能被它的父节点直接照射到,经过
再连接到这样的切点并不是最优路径,因为直接通过它父节点连接到该切点的路径更短。如图4所示,可知黑色的切点可以被父节点直接照射到,是
的Brother,故这些切点无效,只有红色的点无法被父节点照射到,NotBrother=1。NotOtherSon表示:该切点只有通过
到起点的路径最短,而通过Openset中其他点到起点的路径要么比较长,要么会碰到障碍物。只有当切点同时满足NotBrother和NotOtherSon两个条件时,才会被放入Openset。最后,对Openset里所有的点进行重新排序,按照该切点到起点的路径长度从小到大排序,该排序只影响上述第2步中的ChooseSun,迭代次数+1。至此,主代码结束,Pathset会存储所有路径,是不是很简单?

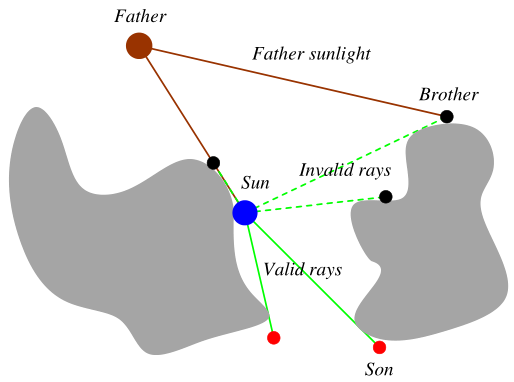
图4 NotBrother机制(黑色的切点是Brother,红色的切点是Son)
为了进一步优化所生成的路径,作者进一步发明了一个双向后端优化机制,即先采用二分法进行前向优化(这个二分法寻找路径和F-RRT*比较类似),再采用二分法反向优化,交替反复优化几次,路径会进一步缩短,尖锐的拐点会被消除。以一个含有6个点的路径为例,其前向优化过程如图5所示,伪代码如Algorithm 3所示。从起点开始,依次选3个点进行处理,直到遍历到终点。先遍历1、2、3,看看1、3两个点是否可以直接相连,如果可以,则用中点代替2,如图5b所示。再遍历2、3、4,同样2、4也可以直接相连,用中点代替3,如图5c所示。再遍历3、4、5,发现4不能用中点代替了,则在4、5之间应用二分法找到4的替代点,如图5d所示。最后,遍历4、5、6,找到5的替代点。1次前向优化结束。然后,从终点到起点,反向应用上述优化方法,前后进行5次优化的过程如图6所示。可以看到,优化后的路径已经达到最优,并贴在障碍物边界上了。这里,我们还对比了一下已有的后端优化方法,即图6b。已有方法通过删除冗余路径点进行优化,相比于本算法会损害对障碍物边界的拟合性。
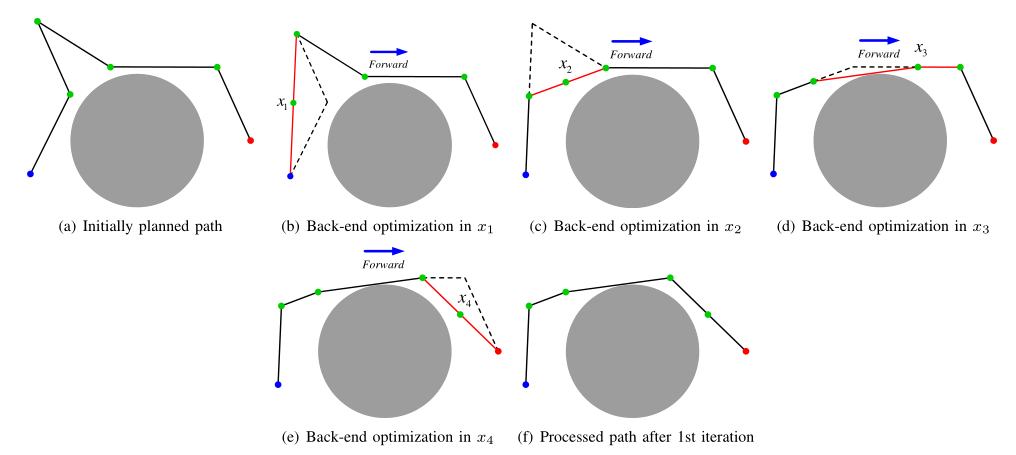
图5 前向优化过程

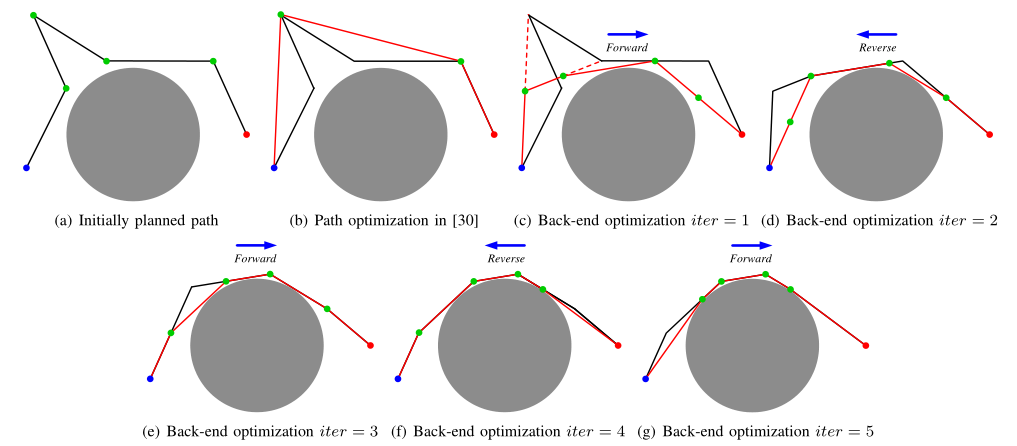
图6 双向优化5次的结果
阳光算法的总体流程已经介绍完了,经过作者证明,该算法具有0(n)的时空复杂度,n是采样点的数目,相比于具有O(nlogn)时空复杂度的RRT*系列算法,路径规划速度要明显提升,尤其是对于非常复杂的环境,甚至可以说有了质的飞跃。下面,我们来看看规划效果吧。
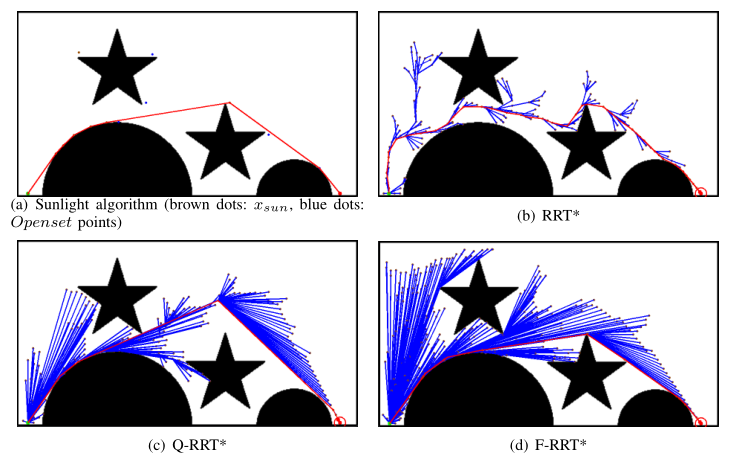
图7 不规则图形场景
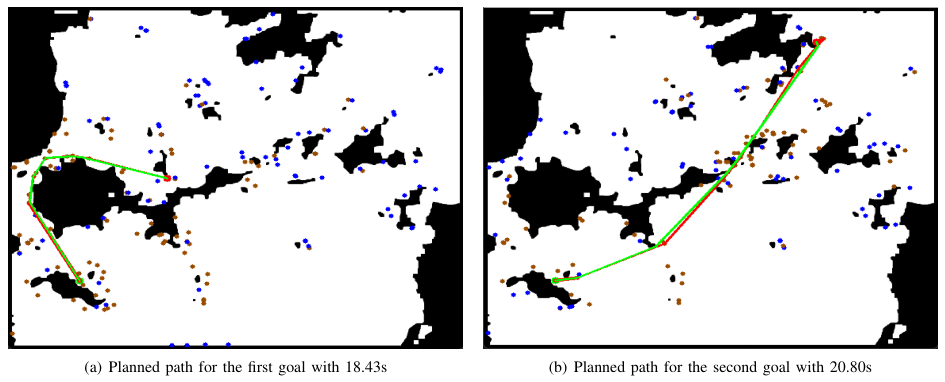
图8 濑户内海真实场景
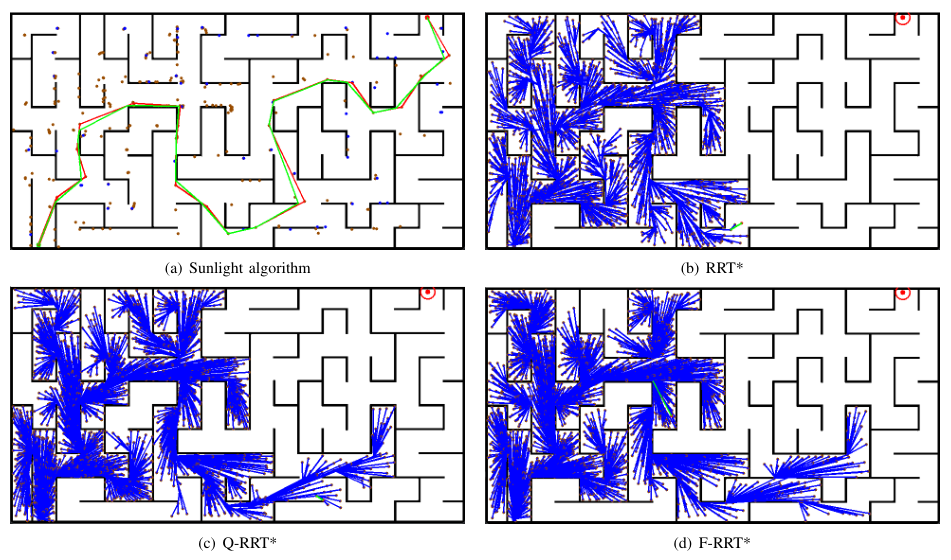
图9 复杂迷宫
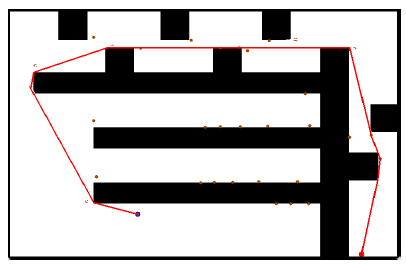
图10 欺骗性的U形障碍物场景
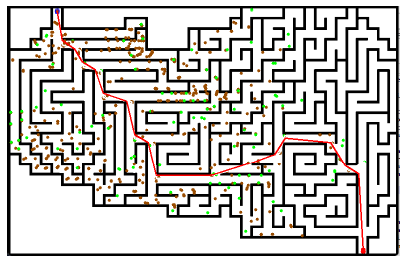
图11 超级复杂迷宫
在进行图9仿真时,阳光算法可以很快找到最优路径,而RRT*系列算法在运行到5分钟时,因为采样点太多而运行得十分缓慢。图11是一个超级复杂迷宫,阳光算法只用了46秒就找到了路径,比人工要快不少。
该算法,目前作者只做到了二维空间,对于三维空间还没有进行测试。如果我们模拟太阳在空间中在发射光线,并按照阳光算法的原理进行路径点采样和筛选,应该也可以实现三维空间的路径规划。此外,该方法只适用于寻找最短距离路径,不适用于含有其他优化目标的路径规划任务。
————————————————— 转载请注明出处 ——————————————————


