opencv卡尺测量工具（圆拟合、直线拟合）_opencv 卡尺

        前段时间在做项目时，偶然接触到Halcon的卡尺测量工具的一些组件，发现还挺好用的，不管是在拟合直线还是在拟合圆时，都有着不错的 精度效果。可惜opencv中没有这些组件，和大多数人一样，疯狂的Google卡尺测量工具，试图找到往上公开的源码，但是到头来发现好像是徒劳的，没有免费开源的源码让你使用。最终还是乖乖的去学习其原理，尝试复现。好在经过几天的尝试，终于复现出来了。下面和各位朋友分享一下原理，来互相学习一下。

        一、原理

        其实这个原理也很简单，就是在寻找边缘的一个过程。只不过他首先对这一组像素，先进行投影处理，然后拟合成函数，然后计算一阶导的峰值，从而得到所需的边缘点。如果在峰值位置再加入一个插值或者拟合处理，即可获取边缘的亚像素位置。

        最终，将所有卡尺矩形框内的边缘点进行直线拟合或者圆拟合，即可得到我们所需的结果。拟合方法可选择最小二乘或者RANSAC。

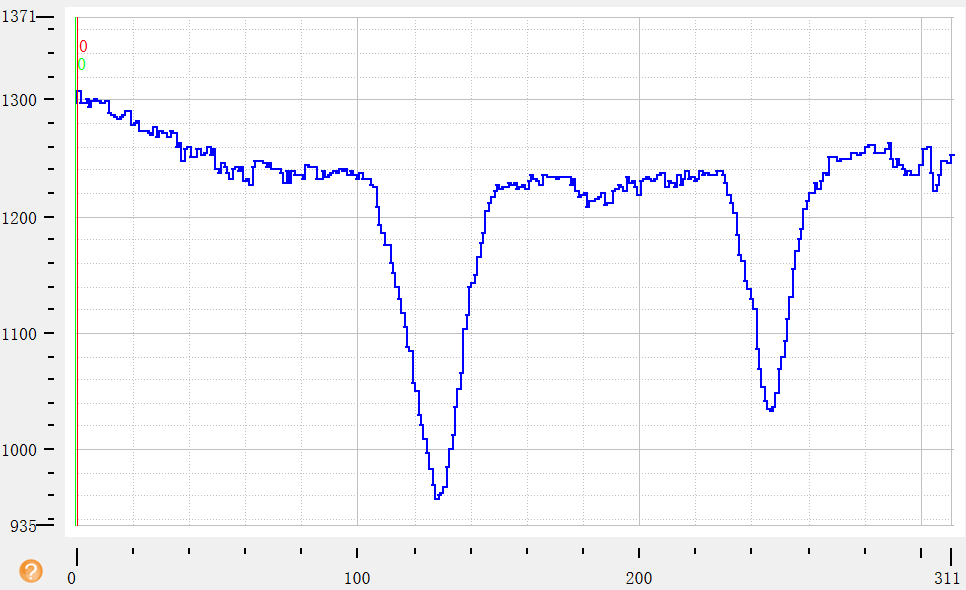
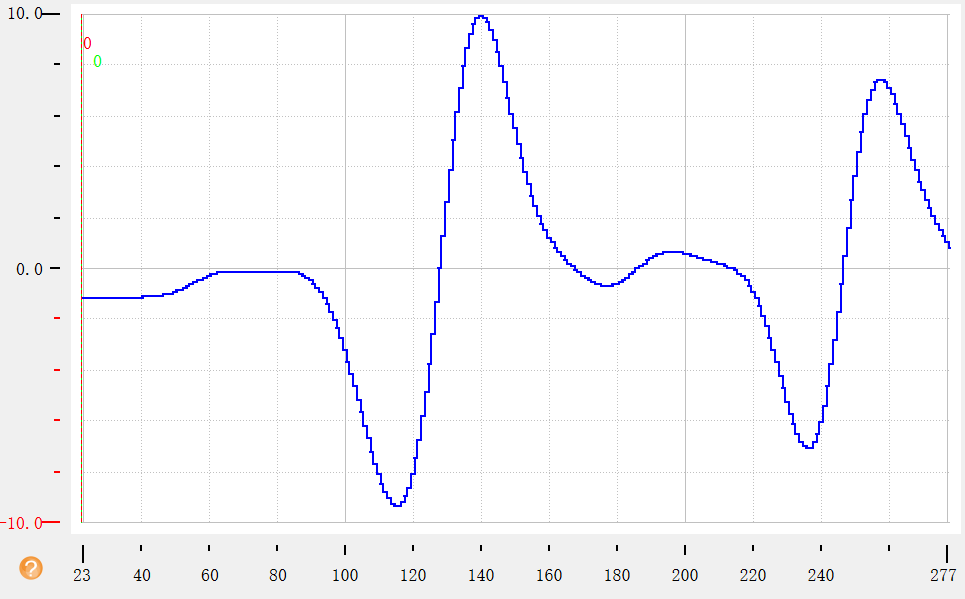
 边缘像素直方图变化

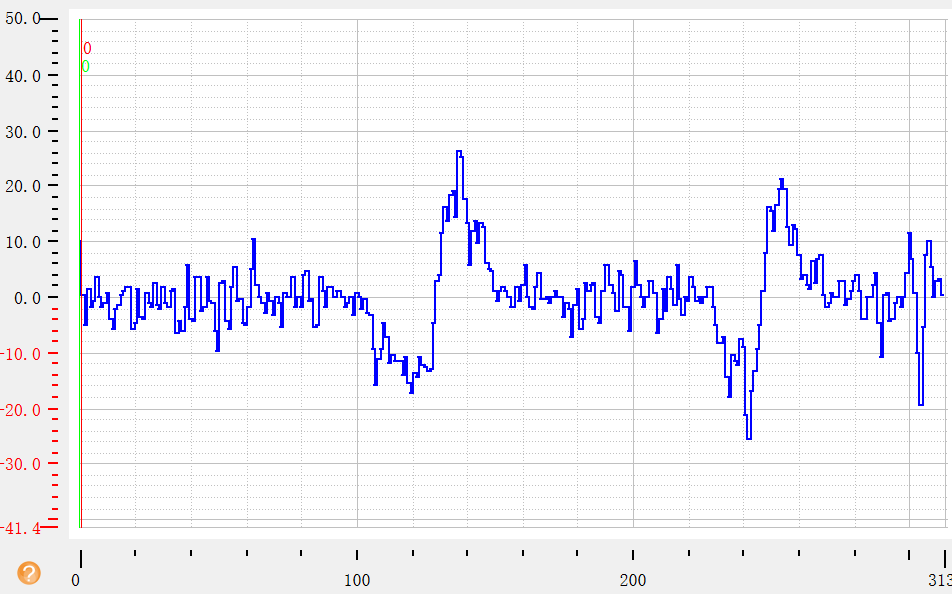
一阶导变化情况 

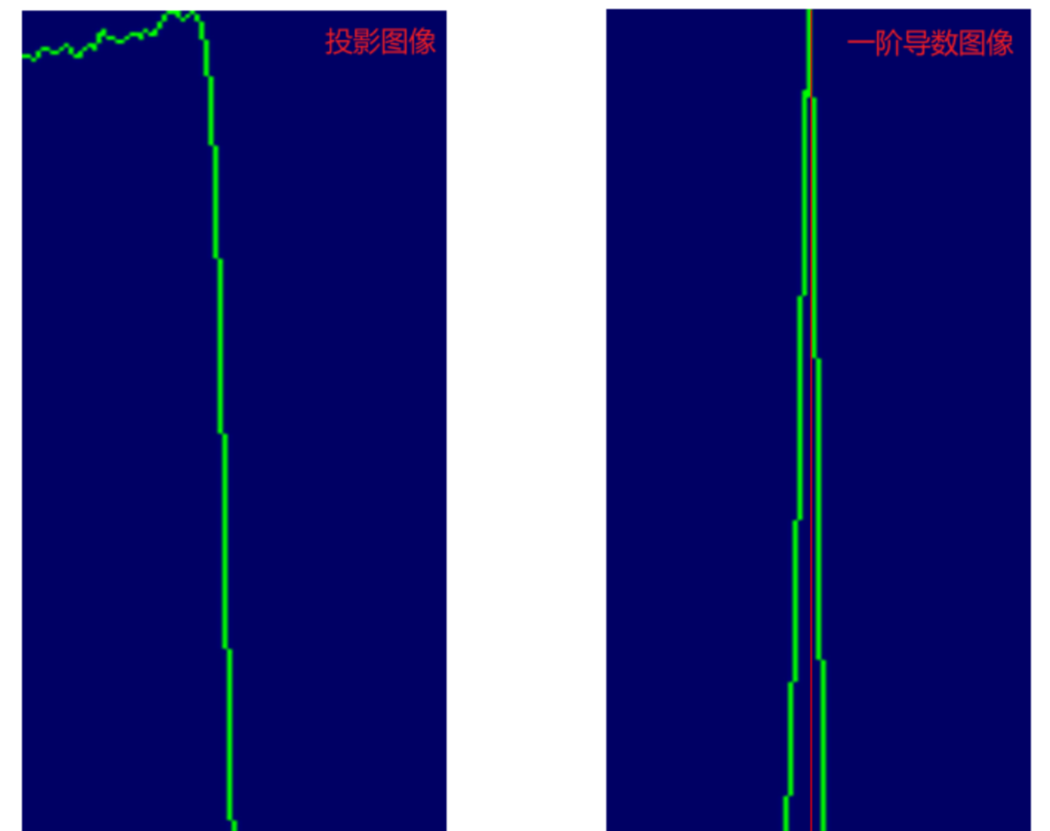
或者更直观一点，借鉴一下这位博主的图像。基于OpenCV实现，仿Halcon卡尺工具_opecv 卡尺找线-CSDN博客

 二、技术难点

        如果要实现这个功能，有以下几步。

1.将卡尺矩形框内的像素进行沿着矩形框方向进行投影，然后对投影像素进行函数拟合。

或者不进行投影计算，直接对矩形框中心的那单列像素进行函数拟合。

2.对拟合的函数进行高斯平滑（可过滤掉噪点）

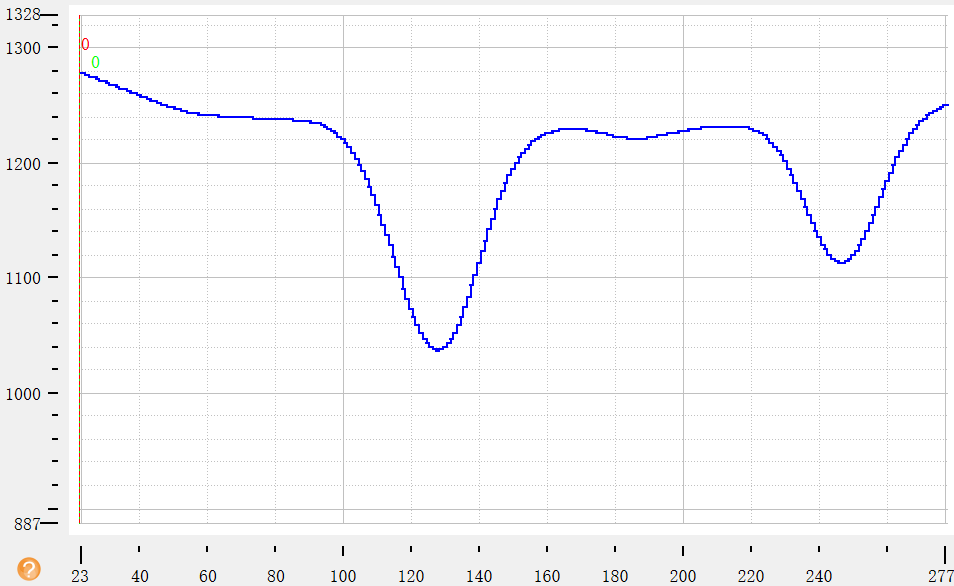
3.计算一阶导，（也可以自己进行计算二阶导）

这部分halcon里面有封装好的算子，可直接修改参数得到满意的效果。但是如果要使用opencv复现，那可能不太好处理，这里我把这部分实现的源码贴一下，互相学习，也帮忙指出我代码中有什么不合理的地方。

class Function1D {public:// 构造函数，接收两个向量作为参数：x 和 y 值Function1D(const std::vector& x_values, const std::vector& y_values): data(x_values.size()) {if (x_values.size() != y_values.size()) {throw std::invalid_argument(\"X and Y value arrays must be of the same size.\");}for (size_t i = 0; i < x_values.size(); ++i) {data[i] = std::make_pair(x_values[i], y_values[i]);}}// 获取函数的大小size_t size() const {return data.size();}// 根据索引获取 (x, y) 对std::pair get(size_t index) const {if (index >= data.size()) {throw std::out_of_range(\"Index out of range.\");}return data[index];}// 打印函数内容void print() const {for (const auto& point : data) {std::cout << \"x: \" << point.first << \", y: \" << point.second << std::endl;}}// 高斯平滑函数static double gaussian(double x, double sigma) {return exp(-0.5 * pow(x / sigma, 2)) / (sigma * sqrt(2 * CV_PI));}// 应用高斯平滑Function1D smoothGauss(double sigma) const {int windowSize = static_cast(ceil(3 * sigma));if (windowSize % 2 == 0) ++windowSize;std::vector kernel(2 * windowSize + 1);double sum = 0.0;for (int i = -windowSize; i <= windowSize; ++i) {kernel[i + windowSize] = gaussian(i, sigma);sum += kernel[i + windowSize];}for (auto& weight : kernel) {weight /= sum;}std::vector new_x(data.size());std::vector new_y(data.size());for (size_t i = 0; i < data.size(); ++i) {new_x[i] = data[i].first;double smoothedY = 0.0;for (int j = -windowSize; j = 0 && neighborIndex < static_cast(data.size())) {smoothedY += data[neighborIndex].second * kernel[j + windowSize];}else {smoothedY += data[i].second * kernel[j + windowSize];}}new_y[i] = smoothedY;}return Function1D(new_x, new_y);}// 计算导数Function1D derivate() const {if (data.size() < 2) {throw std::runtime_error(\"Cannot compute derivative for a function with less than 2 points.\");}std::vector new_x(data.size());std::vector new_y(data.size());for (size_t i = 0; i smoothGauss(sigma);// 计算一阶导数Function1D firstDeriv = smoothedFunc.derivate();// 对一阶导数再次进行高斯平滑Function1D smoothedFirstDeriv = firstDeriv.smoothGauss(sigma);// 计算二阶导数Function1D secondDeriv = smoothedFirstDeriv.derivate();return secondDeriv;}std::vector<std::pair> data; // 存储 (x, y) 对private:};

        三、拟合

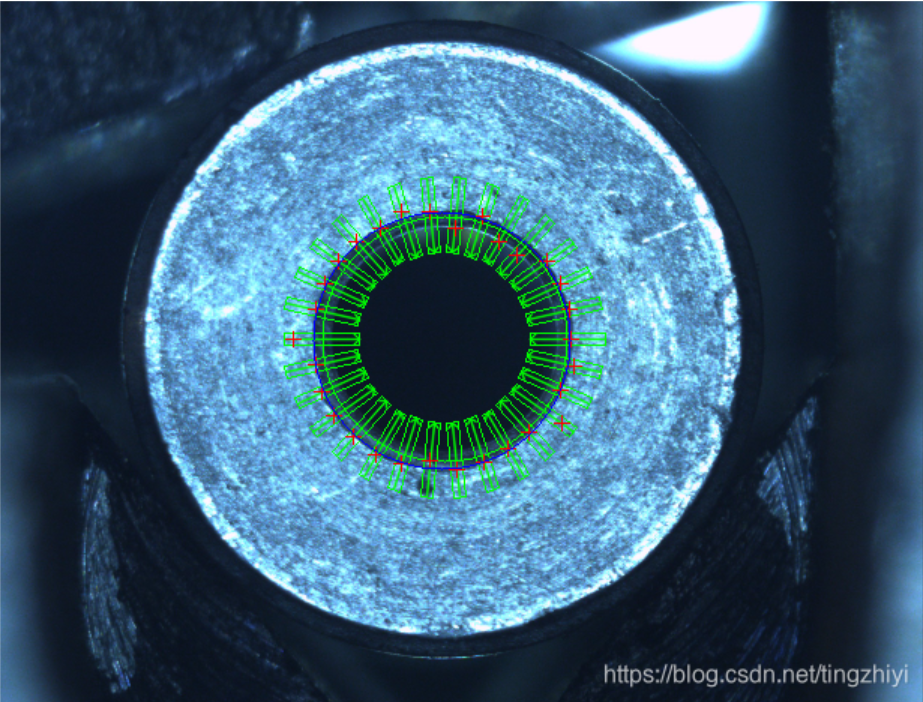
通过一阶导处理后，可以计算出每个卡尺矩形框内的边缘点位置，将这些边缘点进行直线拟合或者圆拟合，即可活动最终的效果。我的代码里面选用的ransac拟合方法。Ransac方法对噪声不敏感，最小二乘对噪声比较敏感。

四、后话

我看网上还有一些拟合椭圆的等等，其内部原理差不多，这部分正在开发中，再有一天时间，也开发出来了。