KNN算法

技术文档

KNN（K-Nearest Neighbors，K 近邻）是机器学习中最经典、最直观的算法之一，属于监督学习范畴，广泛应用于分类、回归任务。

一、KNN 算法概述

KNN 的核心逻辑可以用一句话概括：“物以类聚，人以群分”。对于一个未知类别（或数值）的样本，通过寻找它 “最近的 K 个邻居”，并根据邻居的 “投票”（分类）或 “平均”（回归）来确定该样本的结果。

决策规则：

分类：统计K个邻居中最多数的类别作为预测结果。

回归：取K个邻居目标值的平均值作为预测输出。

二、KNN 核心原理详解

1. 核心思想

KNN 的本质是相似性匹配：假设数据集中的样本特征越相似（距离越近），其类别（或数值）也越可能相同。因此，未知样本的结果由其最相似的 K 个已知样本共同决定。

2. 工作流程（以分类任务为例）

KNN 的预测过程可以拆解为 3 个关键步骤：

计算距离：计算未知样本与所有已知样本（训练集）的 “距离”，衡量两者的相似度；

找邻居（即k值）：从已知样本中筛选出与未知样本距离最近的 K 个样本（即 “K 个邻居”）；

投票决策：统计 K 个邻居的类别，未知样本的类别为 “出现次数最多的类别”（多数投票原则）。

三、KNN 的关键要素

KNN 的性能高度依赖 3 个核心要素：距离度量方式、K 值的选择、是否引入权重。

距离度量方式

距离度量决定了 “两个样本有多像”，不同场景需选择合适的度量方式。

距离计算方法
1. 欧氏距离（Euclidean Distance）
2. 曼哈顿距离（Manhattan Distance）

3. 闵可夫斯基距离（Minkowski Distance）

4. 切比雪夫距离（Chebyshev Distance）

5. 马氏距离（Mahalanobis Distance）

6. 余弦相似度（Cosine Similarity）

7. 汉明距离（Hamming Distance）

8. 杰卡德距离（Jaccard Distance）

9. 布雷叶距离（Bray-Curtis Distance）

10. 马氏重合距离（Mahalanobis–Ovchinnikov Distance）

我们常运用欧式距离，欧式距离的适用场景是连续特征，各维度尺度一致的场景。它的运算公式是：

二维空间的公式

三维空间的公式

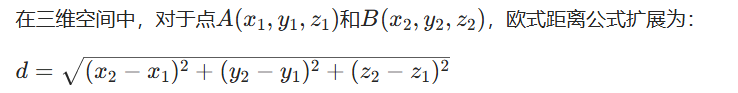
n维空间的公式

K 值的选择

K 值是 KNN 算法中一个非常关键的参数，它的选择会直接影响算法的性能。

当 K 值较小时，模型会变得复杂，容易受到噪声数据的影响，可能会导致过拟合。因为此时只考虑了极少数的邻居，一旦这些邻居中有异常值，就会对预测结果产生很大影响。

当 K 值较大时，模型会变得简单，可能会忽略数据集中的局部特征，导致欠拟合。因为此时考虑的邻居过多，一些距离较远的样本也会参与决策，从而模糊了不同类别之间的界限。

在实际应用中，通常会通过交叉验证的方式来选择合适的 K 值。

是否引入权重

默认情况下，KNN 对所有邻居 “一视同仁”（等权重投票），但更合理的方式是距离越近的邻居权重越大（加权 KNN）。

四、KNN 的优缺点

优点

简单直观：原理易懂，实现难度低，无需复杂的数学推导；

适应性强：无假设前提（如线性可分），对非线性数据友好；

实时更新：新增样本时无需重新 “训练”，直接加入数据集即可；

多分类友好：天然支持多分类任务，无需额外改造。

缺点

计算效率低：预测时需与所有样本计算距离，时间复杂度为O(n)（n为样本数），大数据集下速度慢；

对高维数据敏感：高维特征会导致 “维度灾难”（距离度量失效），需配合降维（如 PCA）；

依赖距离度量：不合理的距离度量会直接导致预测错误；

样本不平衡问题：若某类样本占比极高，K 个邻居中该类可能占多数，导致 bias。

五、实例

鸢尾花的数据测试分析

现给出鸢尾花的训练数据和测试数据，对鸢尾花进行分类，并测试出准确率。

用 Python 的scikit-learn库，基于鸢尾花数据集实现 KNN 分类

通过n_neighbors参数控制邻居数量（K值），默认K=5。

代码实现：

import pandas as pdfrom sklearn.neighbors import KNeighborsClassifiertrain_data = pd.read_excel(\'鸢尾花测试数据.xlsx\')test_data = pd.read_excel(\'鸢尾花训练数据.xlsx\')train_X = train_data[[\'萼片长(cm)\',\'萼片宽(cm)\',\'花瓣长(cm)\',\'花瓣宽(cm)\']]train_y = train_data[[\'类型_num\']]knn = KNeighborsClassifier(n_neighbors=5)knn.fit(train_X,train_y)train_predict=knn.predict(train_X)score=knn.score(train_X,train_y)print(score)test_X = test_data[[\'萼片长(cm)\',\'萼片宽(cm)\',\'花瓣长(cm)\',\'花瓣宽(cm)\']]test_y = test_data[[\'类型_num\']]test_predict=knn.predict(test_X)score=knn.score(test_X,test_y)print(score)

KNN算法

一、KNN 算法概述