动态规划(dynamic programming)
动态规划(dynamic programming)是将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。
一、初识动态规划
爬楼梯
给定一个共有n阶的楼梯,你每步可以上 1 阶或者 2 阶,请问有多少种方案可以爬到楼顶?
如图所示,对于一个 3 阶楼梯,共有 3 种方案可以爬到楼顶。
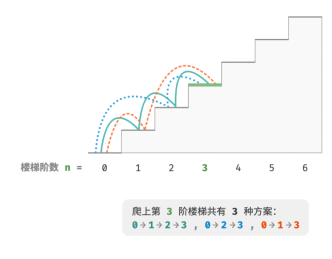
我们通过回溯法穷举出所有可能性,具体思路为从第0阶开始,然后我们前进1阶或者2阶,然后再在这个对应的台阶前进1阶或者2阶。也就是说我们每次前进都可能是1阶或者2阶,然后最终可以到达目标阶位,方案数就加一,超过就减去。
代码如下:
#回溯穷举法def backtrack(choices:list[int],state:int,n:int,res:list[int]) -> int: if state == n: res[0]+=1 for choice in choices: if state + choice > n: continue backtrack(choices, state + choice, n, res)def climbing_stairs_backtrack(n:int) ->int: choices = [1,2] state =0 res = [0] backtrack(choices,state,n,res) return res[0]n=int(input())print(climbing_stairs_backtrack(n)) 这是代码逻辑树,可以帮助理解。
方法一 暴力搜索
通过以上的了解,我们对题目有了一个深刻的认识,然后让我们分解一下这个题目,设爬到第i阶上有dp[i]种解决方案,那么dp[i]就是原问题,dp[i-1],dp[i-2],...dp[2],dp[1]就是子问题,既然我们每次只能上一到两阶,那么在第i阶前一轮的位只能是第i-1阶或者第i-2阶,。换句话说,我们只能从第 i − 1 阶或第 i − 2 阶迈向第i阶。那么我们就可以知道想算出第i阶的方案数,就可以先算出i-1阶和i-2阶的方案数,即dp[i]=dp[i-1]+dp[i-2],这意味着在爬楼梯问题中,各个子问题之间存在递推关系,原问题的解可以由子问题的解构建得来。比如dp[3]=dp[2]+dp[1]=2+1=3。
代码如下:
#暴力搜索-递归def dfs(i:int) -> int: if i == 1 or i == 2: return i count = dfs(i-1) + dfs(i-2) return countdef climbing_stairs_dfs(n:int) ->int: return dfs(n)n = int(input())print(climbing_stairs_dfs(n))方法二:记忆化搜索
我们可知,在暴力搜索的情况下,有子问题是重复计算的,对于重叠的子问题,我们期望只计算一次,此时我们可以通过一个列表来存储计算过的子问题,并且在搜索过程中把重复的子问题给剪枝。
当我们首次计算dp[i]的时候,可以把dp[i]存储在mem[i]中,以便后续使用。
当我们再次需要计算dp[i]的时候,我们就可以从mem[i]中搜索结果,从而避免重叠子问题。
代码如下:
def dfs(i: int, mem:list[int]) ->int: if i == 1 or i == 2: return i if mem[i] != -1: return mem[i] count = dfs(i - 1, mem) + dfs(i - 2, mem) mem[i] = count return countdef climbing_stairs_dfs_mem(n: int) ->int: mem = [-1] * (n + 1) return dfs(n , mem)n = int(input())print(climbing_stairs_dfs_mem(n))
方法三:动态规划
我们仔细观察不难发现,记忆化搜索是一种“从顶至底”的方法,也就是说,这个方法从原问题递归到子问题,层层递进,直至最小子问题。
动态规划算法,恰恰相反,是一种“从底到顶”的方法,从最小的子问题,迭代到更大的子问题,直到原问题的结。
在记忆化搜索和暴力搜索中,我们需要通过递归的方式,一步一步从原始问题到最小子问题递归出最终结果,然而,动态规划算法中,我们是从最底层向上迭代,避免了递归栈。
代码如下:
#动态规划def climbing_stairs_dp(n:int) -> int: if n == 1 or n == 2: return n dp = [0] * (n + 1) dp[1],dp[2] = 1,2 for i in range(3, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[n]n = int(input())print(climbing_stairs_dp(n))空间优化:
我们再继续观察如下式子
dp[3]=dp[2]+dp[1],
dp[4]=dp[3]+dp[2],
.........
dp[i-2]=dp[i-3]+dp[i-4],
dp[i-1]=dp[i-2]+dp[i-3],
dp[i]=dp[i-1]+dp[i-2],
不难发现,dp[i]只与dp[i-1]和dp[i-2]有关,我们无需用dp[i]来存储所有子问题的结,只需要两个变量不断向前滚动迭代即可,代码如下:
def climbing_stairs_comp(n:int) -> int: if n == 1 or n == 2: return n a,b = 1,2 for _ in range(3, n + 1): a,b = a,b + a return bn = int(input())print(climbing_stairs_comp(n))四种情况复杂度分析
方法名称
时间复杂度
空间复杂度
1. 暴力搜索
O(2ⁿ)
O(n)
2. 记忆化搜索
O(n)
O(n)
3. 动态规划
O(n)
O(n)
4. 空间优化
O(n)
O(1)
二、动态规划特性
第一节我们认识到动态规划在重复子问题中的用途,其实动态规划还有两种特性,最优子结构和无后效性。
- 最优子结构
首先我们修改一下问题,如下
给定一个楼梯,你每步可以上 1 阶或者 2 阶,每一阶楼梯上都贴有一个非负整数,表示你在该台阶上所需要付出的代价。给定一个非负整数数组cost,其中 cost[i] 表示在第 i 个台阶需要付出的代价,cost[0]为地面(起始点)。请计算最少需要付出多少代价才能到达顶部?
若第 1、2、3 阶的代价分别为 1、10、1 ,则从地面爬到第 3 阶的最小代价为 2 。
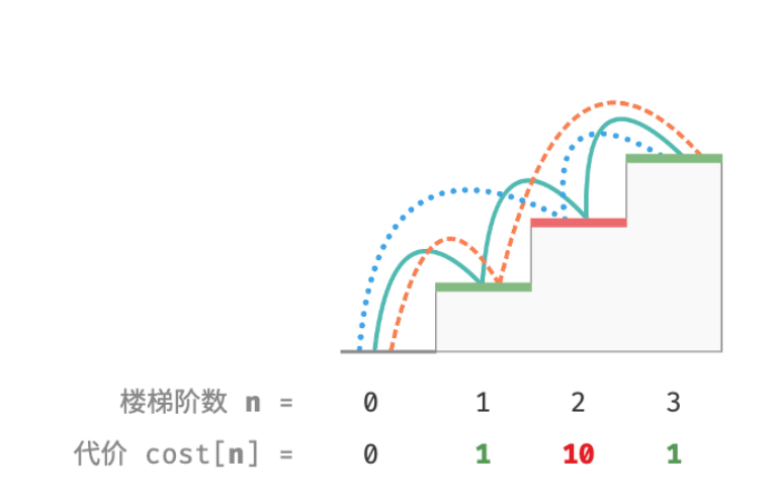
设 dp[i]为爬到第 i 阶累计付出的代价,由于第 i 阶只可能从 i − 1 阶或 i − 2 阶走来,因此 dp[i] 只可能等于 dp[i - 1] + cost[i] 或 dp[i - 2] + cost[i] 。为了尽可能减少代价,我们应该选择两者中较小的那一个:
dp[i] = min{dp[i-1], dp[i-2]} + cost[i]
根据状态转移方程,以及初始状态 dp[1]=cost[1] 和 dp[2]=cost[2] ,我们就可以得到动态规划代码:
def min_cost_climbing_stairs_dp(cost: list[int]) ->int: n = len(cost) - 1 if n == 1 or n == 2: return cost [n] dp = [0] * (n + 1) dp[1],dp[2] = cost[1],cost[2] for i in range(3, n + 1): dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i] return dp[n]空间优化代码:
def min_cost_climing_stairs_comp(cost: list[int]) ->int: n = len(cost) - 1 if n == 1 or n == 2: return cost [n] a, b = cost[1], cost[2] for i in range(3, n + 1): a, b = b, min(a, b) + cost[i] return bn = int(input())cost = [0, 1, 10, 1]print(min_cost_climing_stairs_comp(cost))
实现过程图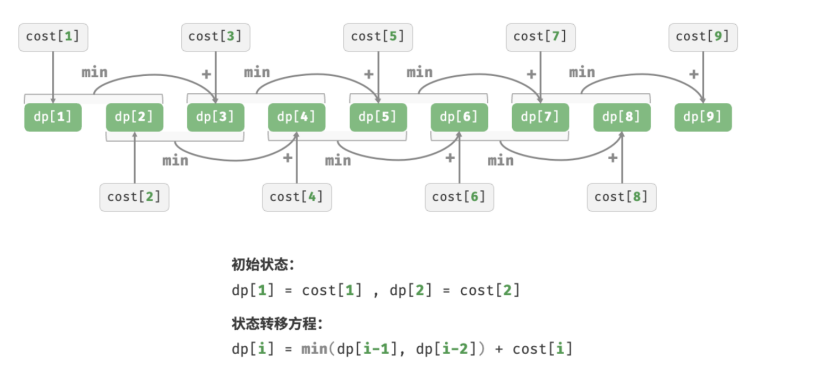
最后,总结一下最优子结构的含义:原问题的最优解是从子问题的最优解构建得来的,同时我认为本质其实还是将一个问题分成多个子问题,只是分给子问题的“权”不一样,再多一个比较的过程。
2.无后效性
那什么是无后效性呢?给定一个确定的状态,它的未来发展只与当前状态有关,而与过去经历的所有状态无关。
以爬楼梯问题为例,给定状态 i ,它会发展出状态 i + 1 和状态 i + 2 ,分别对应跳 1步和跳 2 步。在做出这两种选择时,我们无须考虑状态 i 之前的状态,它们对状态 i 的未来没有影响。
然而,我们通过给爬楼梯的题目再加一个约束,如下:
给定一个共有 n 阶的楼梯,你每步可以上 1 阶或者 2 阶,但不能连续两轮跳 1 阶,请问有多少种方案可以爬到楼顶?
当爬上第 3 阶时,现在仅剩 2 种可行方案,其中连续三次跳 1 阶的方案不满足约束条件,因此被舍弃。
在该问题中,如果上一轮是跳 1 阶上来的,那么下一轮就必须跳 2 阶。这意味着,下一步选择不能由当前状态(当前所在楼梯阶数)独立决定,还和前一个状态(上一轮所在楼梯阶数)有关。
我们不难发现,这个问题已经无法满足无后效性,也就不满足状态转移方程dp[i]=dp[i-1]+dp[i-2]。
那我们应该如何实现呢?我们需要扩展定义,状态 [i, j] 表示处在第 i 阶并且上一轮跳了 j 阶,其中 j ∈ {1, 2} 。此状态定义有效地区分了上一轮跳了 1 阶还是 2 阶,我们可以据此判断当前状态是从何而来的。
当上一轮跳了 1 阶时,上上一轮只能选择跳 2 阶,即dp[i, 1] 只能从dp[i−1, 2] 转移过来。
当上一轮跳了 2 阶时,上上一轮可选择跳 1 阶或跳 2 阶,即 dp[i 2] 可以从 dp[i−2, 1] 或 dp[i−2, 2]转移过来。
在该定义下,dp[i, j] 表示状态 [i, j] 对应的方案数。此时状态转移方程为:
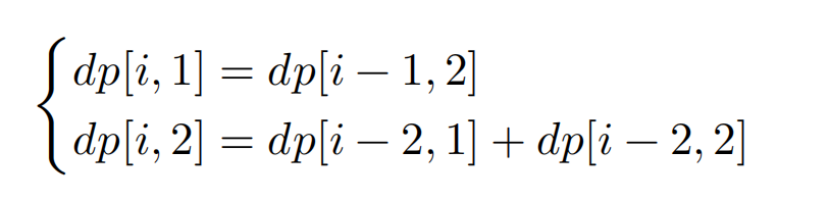
约束下的递推关系:
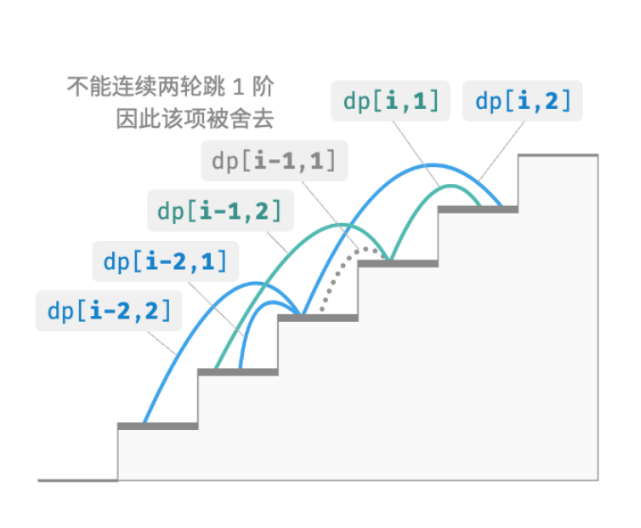
代码如下:
def climbing_stairs_constraint_dp(n: int) -> int: if n == 1 or n == 2: return n dp = [[0] * 3 for _ in range(n + 1)] dp[1][1],dp[1][2] = 1, 0 dp[2][1],dp[2][2] = 1, 0 for i in range(3, n + 1): dp[i][1] = dp[i - 1][2] dp[i][2] = dp[i - 2][1] + dp[i - 2][2] return dp[n][1] + dp[n][2]n=int(input())print(climbing_stairs_constraint_dp(n))本文参考了hello算法-python版中的内容,图片来源于书或者网络。


