【算法深度探索】动态规划之旅(1)：挑战OJ题海，解锁15道经典难题，让你成为DP大师！_动态规划oj

📃博客主页： 小镇敲码人
🚀 欢迎关注：👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨，我自踏雪寻梅香。 万千浮云遮碧月，独傲天下百坚强。 男儿应有龙腾志，盖世一意转洪荒。 莫使此生无痕度，终归人间一捧黄。🍎🍎🍎
❤️ 什么？你问我答案，少年你看，下一个十年又来了 💞 💞 💞

【算法深度探索】动态规划之旅（1）：挑战OJ题海，解锁15道经典难题，让你成为DP大师！

• OJ题1：石子游戏,难度分:1590
• • 题目解析
  • 算法原理
  • 代码实现
  • 使用滚动数组优化
• OJ题2：下降路径最小和 难度分:1573
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题3：最长字符串链 难度分:1599
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题4：最长定差子序列 难度分:1597
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题5：将整数按权重排序 难度分:1507
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题6：使绳子变成彩色的最短时间 难度分:1574
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题7：统计字典序元音字符串的数目 难度分:1519
• • 题目解析
  • 算法原理
  • 代码实现
  • 滚动数组优化
• OJ题8：子数组和的绝对值的最大值 难度分:1542
• • 题目解析
  • 算法原理
  • 代码实现
  • 滚动数组优化
• OJ题9： 个位数字为 K 的整数之和 难度分:1559
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题10：达到末尾下标所需的最大跳跃次数 难度分:1533
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题11：判断是否能拆分数组 难度分:1543 ---区间dp
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题12：推多米诺 难度分：1638
• • 题目解析
  • 算法原理
  • 代码实现
• OJ题13：将字符串翻转到单调递增 难度分:1602
• • 题目解析
  • 算法原理
  • 代码实现
  • 滚动数组优化
• OJ题14：骑士拨号器 难度分:1690
• • 题目解析
  • 算法原理
  • 代码实现
  • 滚动数组优化
• OJ题15：掷骰子等于目标和的方法数 难度分:1654---分组背包
• • 题目解析
  • 算法原理
  • 代码实现
  • 滚动数组优化

前言：本篇博客旨在帮助大家学习和了解DP算法，并熟练的掌握DP算法的原理和一些套路，以题解的形式给出，题目出自力扣平台，后面的数字代表难度分。

OJ题1：石子游戏,难度分:1590

这里是题目链接

题目解析

算法原理

下面我们来尝试使用动态规划来解决这道题。

代码实现

class Solution { public: bool stoneGame(vector<int>& piles) {  //创建dp表 //初始化 //填表 //返回值 int n = piles.size(); vector<vector<int>> dp(n,vector<int>(n)); dp[0][0] = piles[0]; dp[n-1][n-1] = piles[n-1]; for(int i = n-2;i >= 0;i--) for(int j = i;j < n;j++) if(j > 0) dp[i][j] = max(piles[i]-dp[i+1][j],piles[j]-dp[i][j-1]);  return dp[0][n-1] > 0; }};

ak截图：

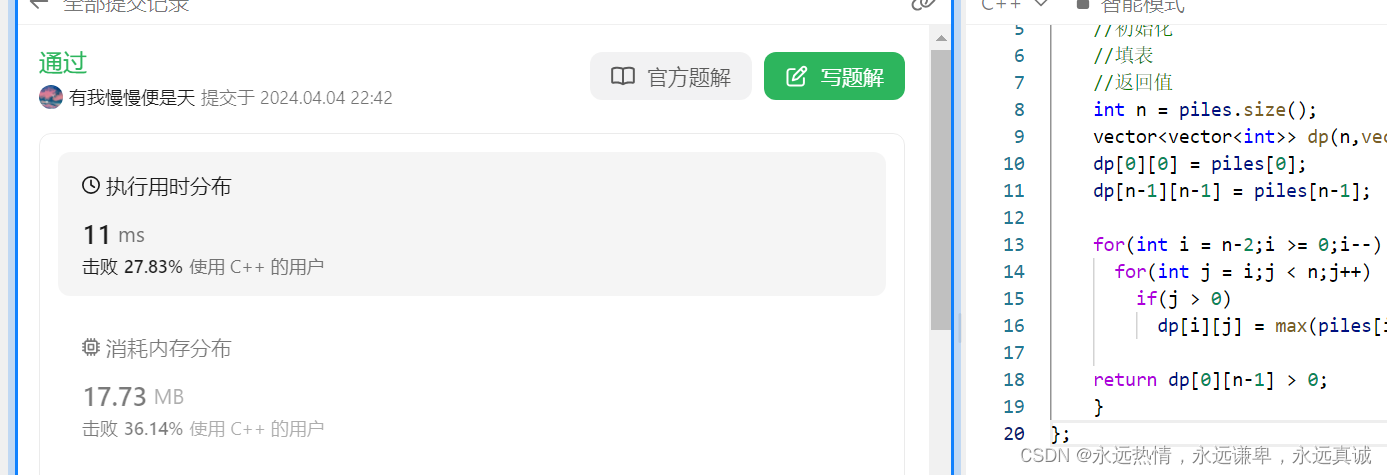
使用滚动数组优化

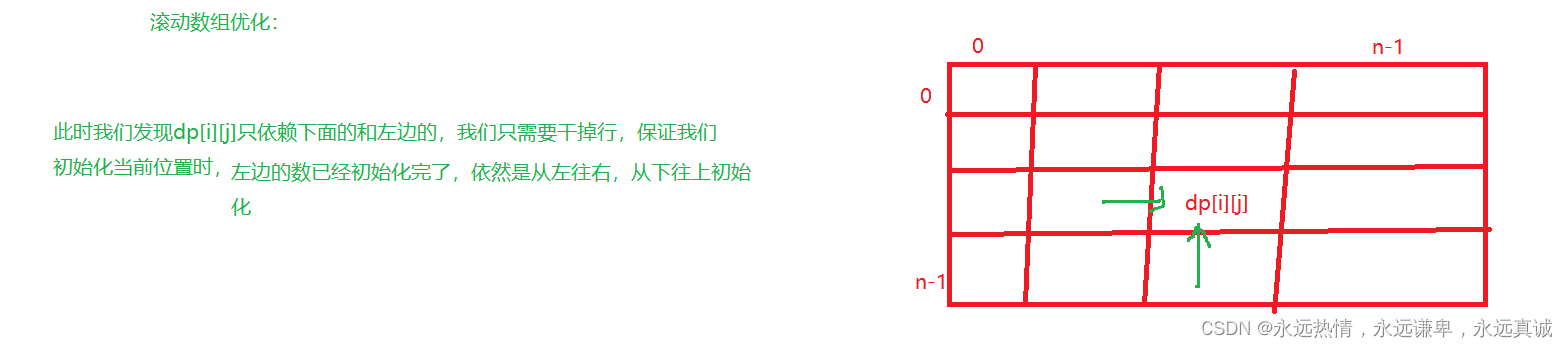
代码实现：

class Solution { public: bool stoneGame(vector<int>& piles) {  //创建dp表 //初始化 //填表 //返回值 int n = piles.size(); vector<int> dp(n); dp[0] = piles[0]; dp[n-1] = piles[n-1]; for(int i = n-2;i >= 0;i--) for(int j = i;j < n;j++) if(j > 0) dp[j] = max(piles[i]-dp[j],piles[j]-dp[j-1]); return dp[n-1] > 0; }};

ak截图：

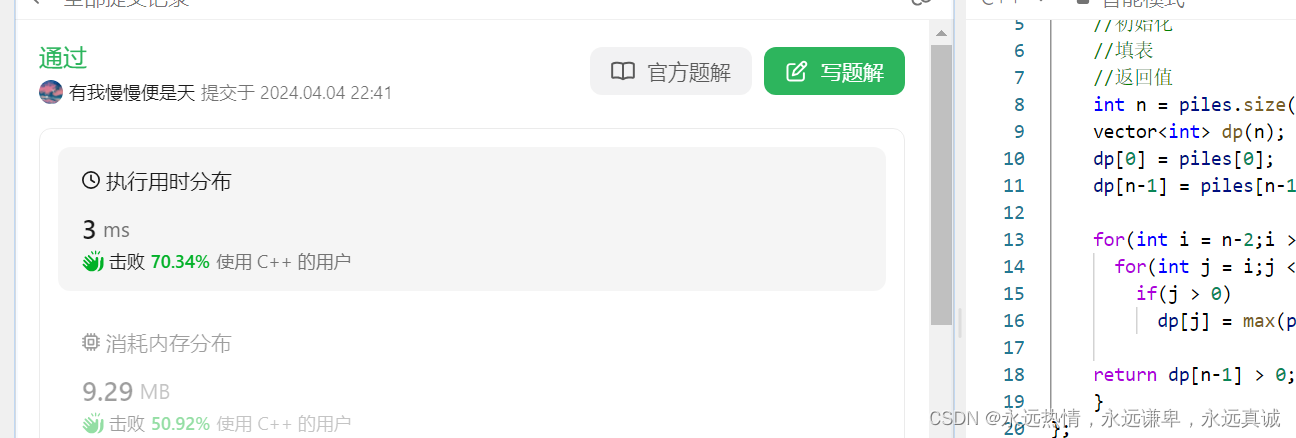
OJ题2：下降路径最小和 难度分:1573

这里是题目链接

题目解析

算法原理

我们尝试使用动态规划来解决一下这道题

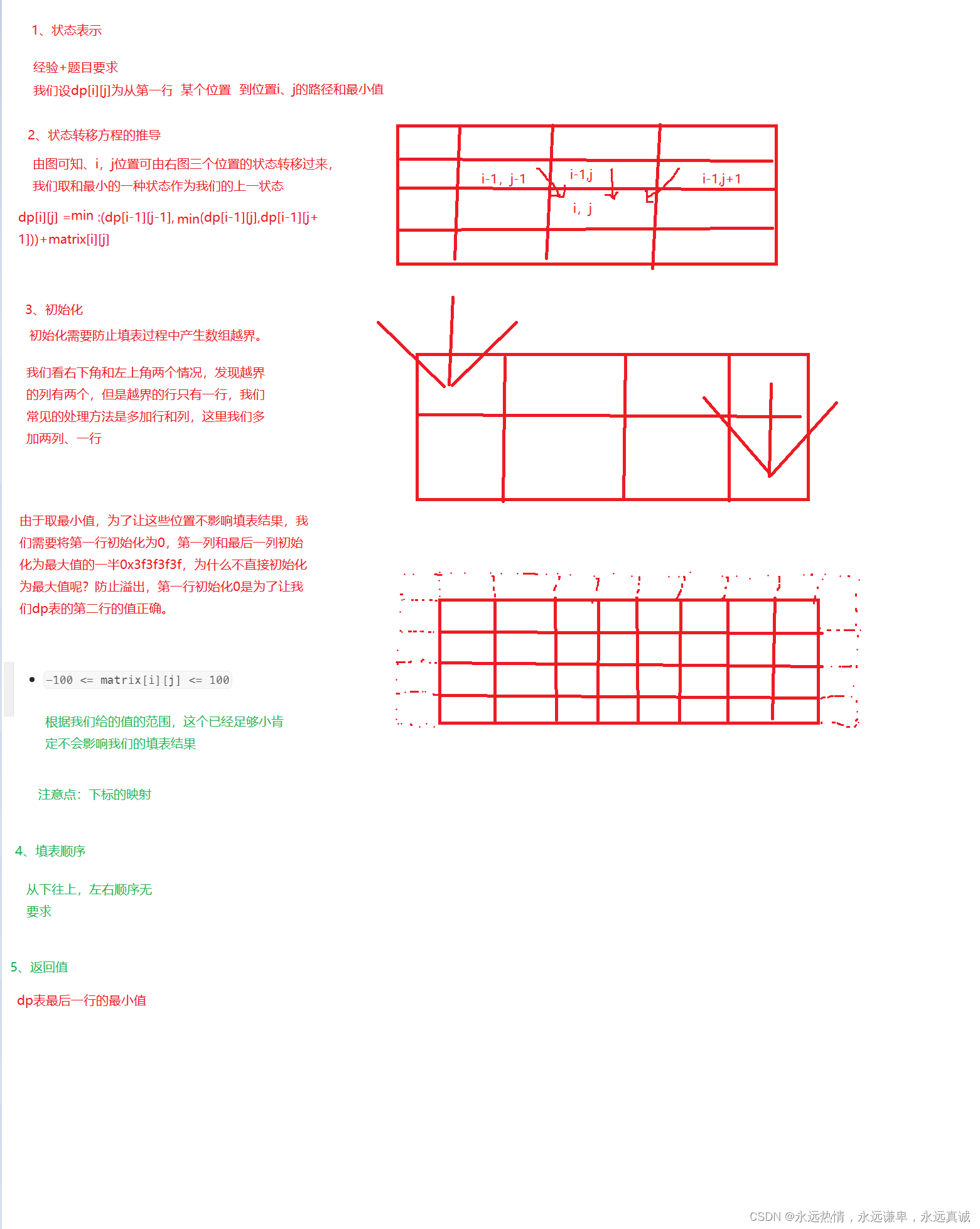
代码实现

class Solution { public: int minFallingPathSum(vector<vector<int>>& matrix) {  //创建dp表 //初始化 //填表 //返回值 int INF = 0x3f3f3f3f; int n = matrix.size(); int m = matrix[0].size(); vector<vector<int>> dp(n+1,vector<int>(m+2,INF)); for(int j = 0;j <= m;++j) dp[0][j] = 0; for(int i = 1;i <= n;++i) for(int j = 1;j <= m;++j) dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1]; int ret = INF; for(int j = 1;j <= m;++j) ret = min(ret,dp[n][j]); return ret; }};

ak截图：

OJ题3：最长字符串链 难度分:1599

这里是题目链接

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

代码实现

int compare(string& a,string& b){  return a.size() < b.size();}class Solution { public: int longestStrChain(vector<string>& words) {  sort(words.begin(),words.end(),compare);//排序 unordered_map<string,int> hash; int n = words.size(); for(int i = 0;i < n;++i) hash[words[i]] = i; vector<int> dp(n,1); int ret = 1; for(int i = 1;i < n;++i) {  for(int j = 0;j < words[i].size();++j) {  string wordprev = words[i].substr(0,j)+words[i].substr(j+1); if(hash.count(wordprev))  dp[i] = max(dp[hash[wordprev]]+1,dp[i]); } ret = max(ret,dp[i]); } return ret; }};

ak截图：

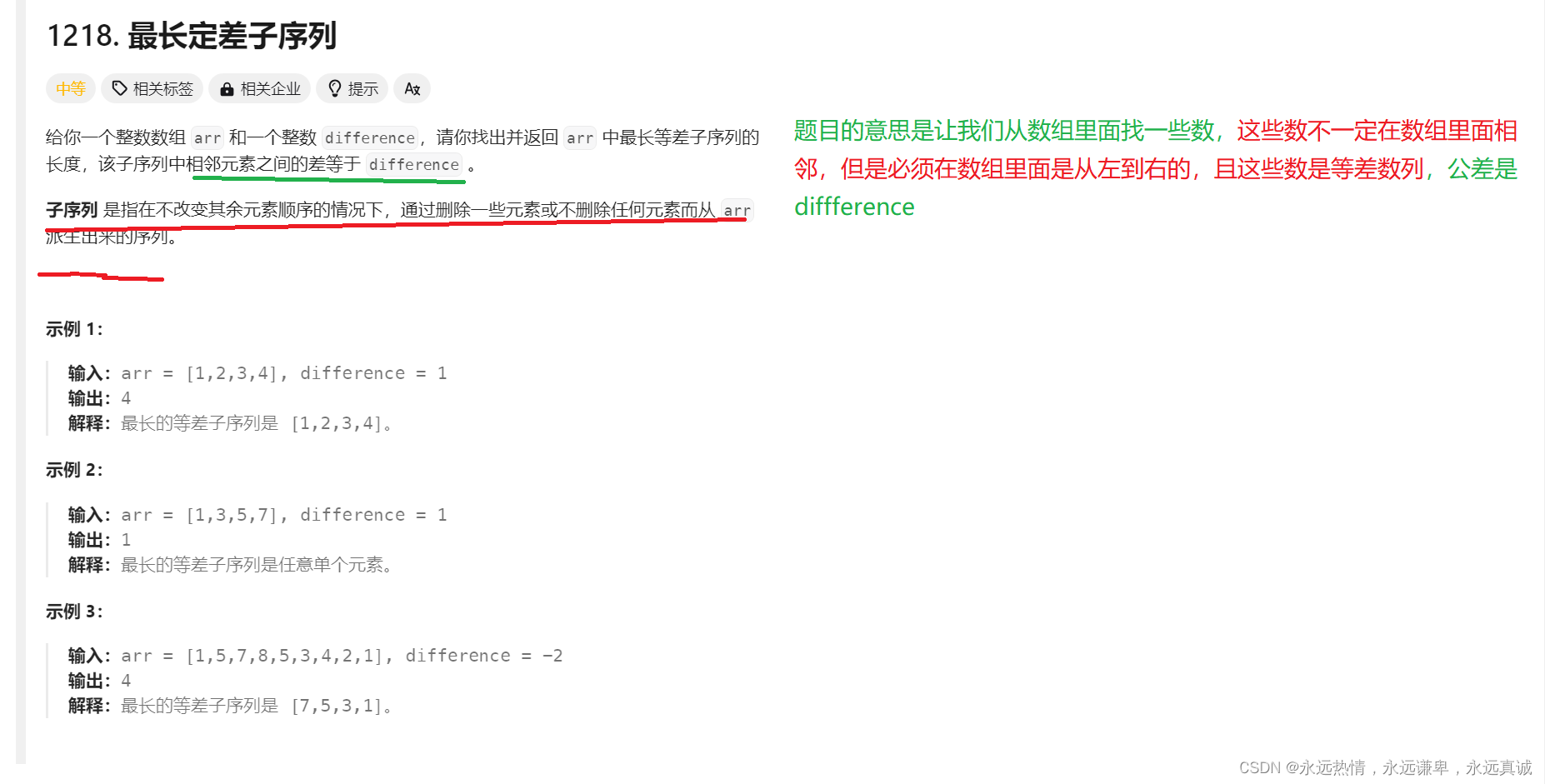
OJ题4：最长定差子序列 难度分:1597

这里是题目链接

题目解析

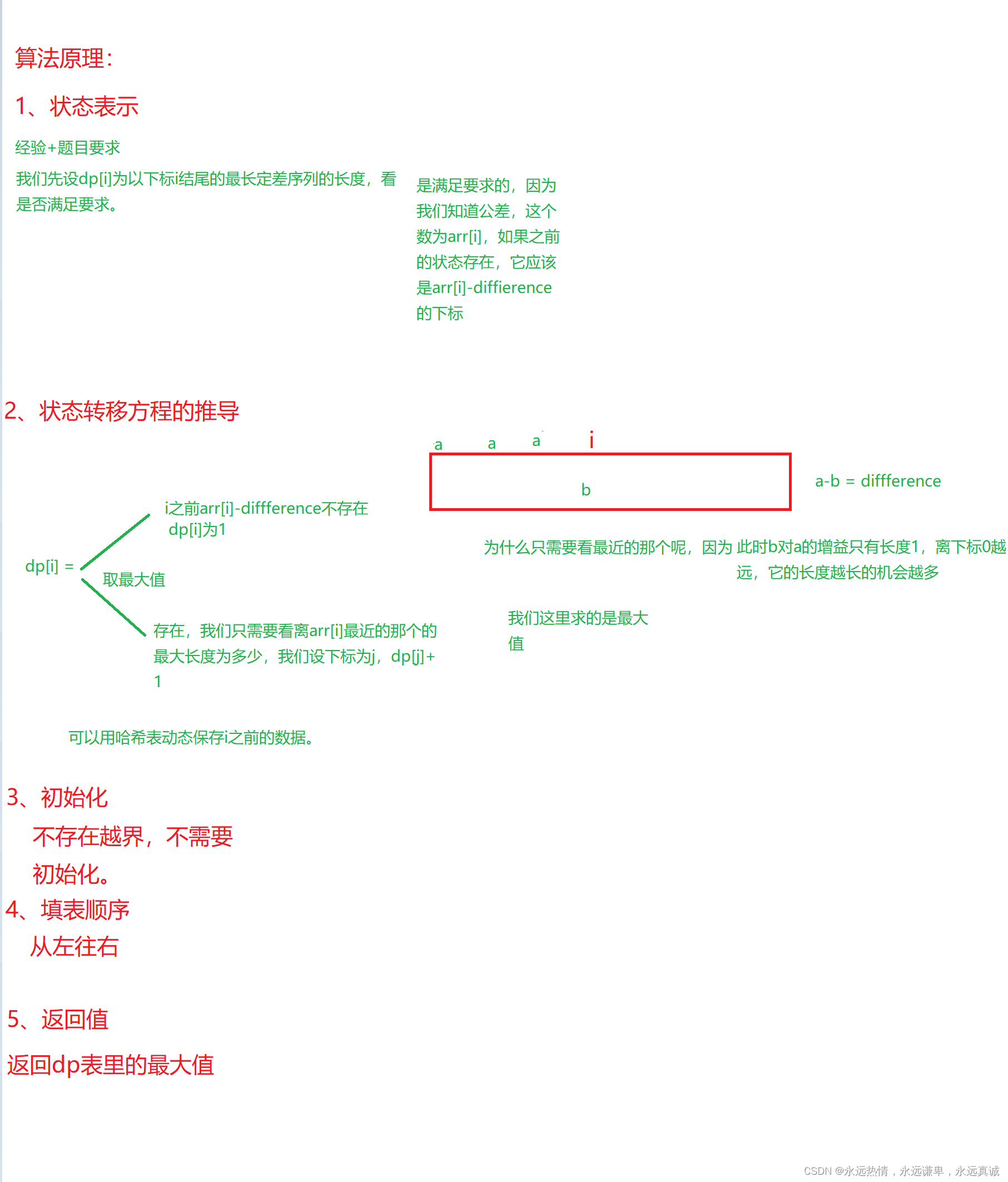
算法原理

代码实现

class Solution { public: int longestSubsequence(vector<int>& arr, int difference) {  int n = arr.size(); unordered_map<int,int> hash;//值-下标 //创建dp表 //初始化 //填表 //返回值 vector<int> dp(n,1); int ret = 0; for(int i = 0;i < n;++i) {  int a = arr[i]; if(hash.count(a-difference)) dp[i] = dp[hash[a-difference]]+1; hash[arr[i]] = i