代码随想录算法训练营Day34|动态规划Part02|62.不同路径、63. 不同路径 II 、343.整数拆分 （可跳过）、96.不同的二叉搜索树 （可跳过）

62.不同路径

代码随想录

视频讲解：动态规划中如何初始化很重要！| LeetCode：62.不同路径_哔哩哔哩_bilibili

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

• 输入：m = 3, n = 7
• 输出：28

示例 2：

• 输入：m = 2, n = 3
• 输出：3

解释： 从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 3：

• 输入：m = 7, n = 3
• 输出：28

示例 4：

• 输入：m = 3, n = 3
• 输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10^9

import java.util.ArrayList;class Solution { public int uniquePaths(int m, int n) { int[][] dp = new int[m][n]; if(m==1 || n==1) return 1; for(int i=0;i<m;i++){ dp[i][0] = 1; } for(int j=0;j<n;j++){ dp[0][j] = 1; } for(int p=1;p<m;p++){ for(int q=1;q<n;q++){ dp[p][q] = dp[p-1][q]+dp[p][q-1]; } } return dp[m-1][n-1]; }}

63. 不同路径 II

视频讲解：动态规划，这次遇到障碍了| LeetCode：63. 不同路径 II_哔哩哔哩_bilibili

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

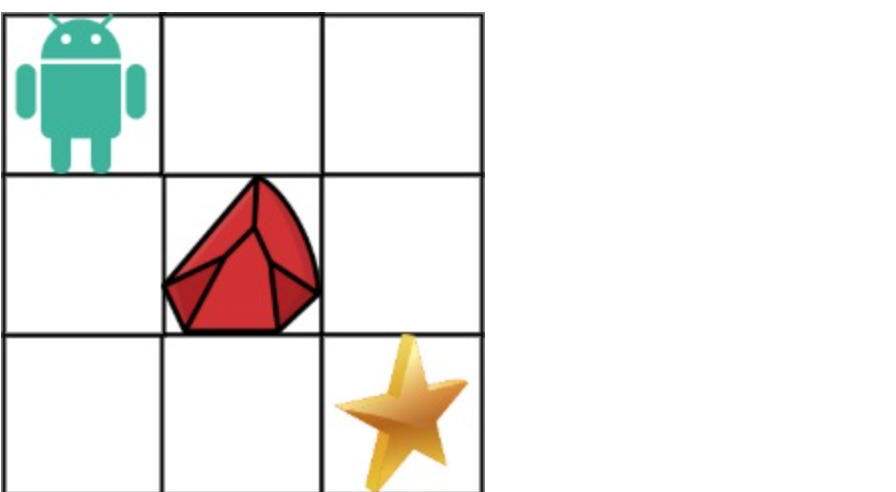
• 输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
• 输出：2 解释：
• 3x3 网格的正中间有一个障碍物。
• 从左上角到右下角一共有 2 条不同的路径：
  1. 向右 -> 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

• 输入：obstacleGrid = [[0,1],[0,0]]
• 输出：1

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

class Solution { public int uniquePathsWithObstacles(int[][] obstacleGrid) { int m = obstacleGrid.length; int n = obstacleGrid[0].length; int[][] dp = new int[m][n]; dp[0][0] = obstacleGrid[0][0]==0 ? 1:0; if(dp[0][0]==0) return 0; for(int i=1;i<m;i++){ dp[i][0] = dp[i-1][0]*Math.abs(obstacleGrid[i][0]-1); } for(int j=1;j<n;j++){ dp[0][j] = dp[0][j-1]*Math.abs(obstacleGrid[0][j]-1); } for(int p=1;p<m;p++){ for(int q=1;q<n;q++){ dp[p][q] = obstacleGrid[p][q]==1 ? 0:dp[p-1][q]+dp[p][q-1]; } } return dp[m-1][n-1]; }}

343.整数拆分 （可跳过）

代码随想录

视频讲解：动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

• 输入: 2
• 输出: 1
• 解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

• 输入: 10
• 输出: 36
• 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
• 说明: 你可以假设 n 不小于 2 且不大于 58。

思路

动态规划没有思考出来，采用另一种数学方法，可以证明把n分为k份时要使得这k个数乘积最大，需要让这k个数之间的差异最小，也就是最大值和最小值最大只能差1.只要确定好分配方法，就可以遍历n的所有组合可能（分为2，3，4，5...份），保留乘积最大值。

class Solution { public int integerBreak(int n) { int res = Integer.MIN_VALUE; for(int i=2;itmp ? res:tmp; } return res; } public int divide(int n,int k){ int mul = 1; int reminder = n%k; int base = n/k; for(int i=0;i0){ mul*= base+1; reminder--; } else{ mul*= base; } } return mul; }}

动态规划最重要的是把递推公式写出来，怎么由前置dp获取后续结果

class Solution { public int integerBreak(int n) { int[] dp = new int[n+1]; dp[2] = 1; for(int i=3;i<=n;i++){ for(int j=1;j<=i/2;j++){ dp[i] = Math.max(dp[i],Math.max(j*(i-j), j*dp[i-j])); } } return dp[n]; }}

96.不同的二叉搜索树 （可跳过）

代码随想录

视频讲解：动态规划找到子状态之间的关系很重要！| LeetCode：96.不同的二叉搜索树_哔哩哔哩_bilibili

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

class Solution { public int numTrees(int n) { int[] dp = new int[n+1]; dp[0] = 1; dp[1] = 1; for(int i=2;i<=n;i++){ for(int j=1;j<=i;j++){ dp[i]+=dp[j-1]*dp[i-j]; } } return dp[n]; }}