深度学习数学基础——线性代数和微积分
目录
1.线性代数
1.1 向量
1.2 矩阵
1.3 范数(norm)
1.4 总结
2. 微积分
2.1 导数和微分
2.2 偏导数
2.3 梯度
2.4 链式法则
2.5 小结
1.线性代数
n维数组,也成为张量(tensor),具有一个轴的张量对应数学上的向量(vector); 具有两个轴的张量对应数学上的矩阵(matrix); 具有两个轴以上的张量没有特殊的数学名称。
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
y = x.reshape(3, 4)或
y = x.reshape(3, -1)
y = x.reshape(-1 ,4)
tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
torch.zeros((2, 3, 4))
注意内部为小括号
几个中括号就是几维张量
tensor([[[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]], [[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]])
tensor([[[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]], [[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]]])
标准高斯分布随机采样
正态分布
torch.randn(3, 4)
主要用于初始化神经网络参数
tensor([[-0.0135, 0.0665, 0.0912, 0.3212], [ 1.4653, 0.1843, -1.6995, -0.3036], [ 1.7646, 1.0450, 0.2457, -0.7732]])
数学运算
需要统一形状
x = torch.tensor([1.0, 2, 4, 8])y = torch.tensor([2, 2, 2, 2])x + y, x - y, x * y, x / y, x ** y
(tensor([ 3., 4., 6., 10.]), tensor([-1., 0., 2., 6.]), tensor([ 2., 4., 8., 16.]), tensor([0.5000, 1.0000, 2.0000, 4.0000]), tensor([ 1., 4., 16., 64.]))
X = torch.arange(12, dtype=torch.float32).reshape((3,4))Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
dim = 0表示按行连结,往下接
dim = 1表示按列连结,往右接
轴0和轴1分别对应行和列,axis=0是沿着轴0去做,而轴0的方向是向下的,这点比较绕,可以理解为想要扩展行数就要向下扩展,扩展列数是向右扩展。所以axis=0给人感受是在求一列的和
y = torch.ones(4, dtype = torch.float32)x, y, torch.dot(x, y)#先相乘再求和torch.sum(x * y)
tensor(6.))
向量暗元素相乘再相加
torch.mv(A , x)
m为matrix , v为vector
二范数torch.norm( x )
一范数torch.abs(x).sum()
1.1 向量
深度学习中向量为列向量,vectors,n维向量x可表示为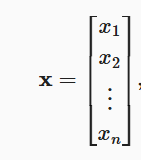 ,其中
,其中是向量的元素,每一个元素代表这个向量不同的指标。比如人的身体状况为x,那么各个元素代表的是可能是他的生命体征、运动时间、血压、血糖等。在代码中用张量tensor索引来访问任意元素。
x[3]tensor(3)向量也有长度,称为向量的维度(dimension),一个向量由n个实值标量组成,可记为![]() 。
。
调用Python内置函数len( )来查看向量的长度。
也可以通过.shape属性来访问向量的长度。
向量或轴的维度用来表示向量或轴的长度,即向量或轴的元素数量。
张量的维度用来表示张量具有的轴数。那么张量某个轴的维度就是这个轴的长度
向量的点乘是标量,每个元素相乘再相加。
1.2 矩阵
矩阵是有用的数据结构:它们允许我们组织具有不同模式的数据。深度学习中用粗体、大写的字母表示矩阵,在代码中表示具有两个轴的张量。
由此想到:向量的张量的维度是1,表示为tensor.Size([4]),矩阵或者2维向量是tensor.Size([2,2])
三维的为tensor.Size([1,2,3])

实例化张量:
A = torch.arange(20).reshape(4,5)tensor([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14], [15, 16, 17, 18, 19]])矩阵的转置,就是沿对角线翻转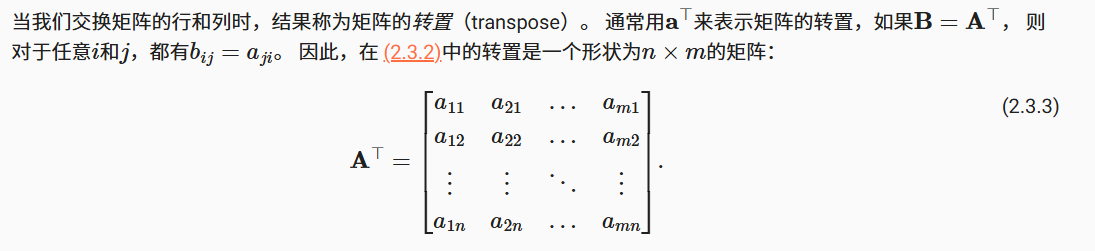
在python中,矩阵的转置为A.T。方阵是特殊的矩阵,对称矩阵的转置还是本身。
两个形状相同的矩阵加法是按元素相加;
两个矩阵按元素乘法的运算叫做:阿达马积(Hadamard product)
而两个矩阵相乘为AB,这个比较常用的。
矩阵特征向量可以理解为矩阵经过空间变换,其中一个方向恒存在,即为特征向量。
矩阵-向量积:A的列维数(沿轴1的长度)必须与x的维数(其长度)相同
A.shape, x.shape, torch.mv(A, x)(torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))1.3 范数(norm)
向量的范数是表示一个向量有多大。这里考虑的大小(size)概念不涉及维度,而是分量的大小。
范数的性质:

二范数: 代码是torch.norm( x )
代码是torch.norm( x )
一范数是向量元素的绝对值之和torch.abs( x ).sum()
F范数,针对矩阵而言,是矩阵元素平方和的平方根。
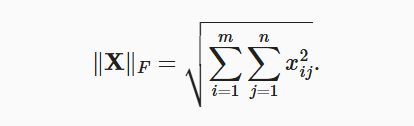
1.4 总结
深度学习里面的线性代数难度不大,重点是运算与范数
-
标量、向量、矩阵和张量是线性代数中的基本数学对象。
-
向量泛化自标量,矩阵泛化自向量。
-
标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。
-
一个张量可以通过
sum和mean沿指定的轴降低维度。 -
两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。
-
在深度学习中,我们经常使用范数,如
范数、
范数和Frobenius范数。
-
我们可以对标量、向量、矩阵和张量执行各种操作
-
广播机制(broadcasting)
2. 微积分
主要是导数微分、偏导数、链式法则、梯度。
-
优化(optimization):用模型拟合观测数据的过程;
-
泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
-
在深度学习中,我们通常选择对于模型参数可微的损失函数。简而言之,对于每个参数, 如果我们把这个参数增加或减少一个无穷小的量,可以知道损失会以多快的速度增加或减少,
2.1 导数和微分


2.2 偏导数

2.3 梯度

2.4 链式法则

2.5 小结
-
微分和积分是微积分的两个分支,前者可以应用于深度学习中的优化问题。
-
导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率。
-
梯度是一个向量,其分量是多变量函数相对于其所有变量的偏导数。
-
链式法则可以用来微分复合函数。


