网站导航
> 技术文档 > 矩阵寻宝奇旅：揭秘最大子矩阵与最大黑方阵的算法奥秘

矩阵寻宝奇旅：揭秘最大子矩阵与最大黑方阵的算法奥秘

网友: 技术文档 2025-07-30 12:59:58

在算法的星河中，矩阵问题犹如一座神秘迷宫。今日，我们将深入探索两颗耀眼的双子星——最大子矩阵与最大黑方阵。前者是动态规划的降维艺术，后者是边界检测的拓扑魔术。它们同处二维空间，却因目标不同走向分岔：一个追求内部总和最大化，一个苛求边界条件完美化。这场对决将揭示算法设计中的核心哲学：问题转化、时空权衡与预处理智慧。准备好你的思维罗盘，我们启程！

博客正文

问题一：最大子矩阵——动态规划的降维打击

给定一个字符串 s 和一个单词列表 wordDict，要求判断是否可以将 s 拆分成字典中的一个或多个单词。例如，输入 s = \"leetcode\"，wordDict = [\"leet\", \"code\"]，输出为 true，因为 s 可以拆分为 \"leet\" 和 \"code\"。

🔍 问题本质
给定一个混杂正负整数的 N×MN×M 矩阵，寻找和最大的连续子矩阵。输出其左上角 (r1,c1)(r1,c1) 和右下角 (r2,c2)(r2,c2) 坐标。

⚙️ 算法核心：从二维到一维的坍缩

  1. 预处理：行前缀和矩阵

    • 构建前缀和数组 pref[i][j]，存储第 ii 行前 jj 个元素之和。

    • 目的：O(1)O(1) 时间计算任意行区间 [ca,cb][ca​,cb​] 的和。

  2. 枚举行对 + Kadane算法

    • 利用前缀和优化，该步骤仅需 O(M)O(M) 时间。

    • Step 3: 在 col_sum 上运行 Kadane算法（一维最大子数组和）：

      • 动态维护当前和 cur_sum、全局最大和 max_sum 及边界索引。

      • 时间复杂度：O(M)O(M)。

  2. 时空复杂度

    • 时间：O(N2×M)O(N2×M)（枚举行对 O(N2)O(N2) × Kadane算法 O(M)O(M)）。

    • 空间：O(M)O(M)（存储压缩后的一维数组）。

🎯 关键洞见

降维思想：将二维问题分解为“枚举行对 + 一维子问题”。Kadane算法在此扮演一维时空隧道，将复杂度从 O(N2M2)O(N2M2) 压缩至 O(N2M)O(N2M)。

详细分析：

  1. 状态定义：定义一个布尔数组 dp，其中 dp[i] 表示字符串 s 的前 i 个字符是否可以拆分成字典中的单词。
  2. 状态转移：
    • 对于每个位置 i，遍历所有可能的单词 word，如果 word 的长度为 len，且 s 的子串 s[i-len:i] 等于 word，并且 dp[i-len] 为 true，则 dp[i] 设为 true。
  3. 初始化：dp[0] = true，表示空字符串可以被拆分。
  4. 结果计算：dp[s.length] 即为答案。

验证示例：

  • 示例1：输入 s = \"applepenapple\"，wordDict = [\"apple\", \"pen\"]，输出为 true。
    • s 可以拆分为 \"apple\"，\"pen\"，\"apple\"。
  • 示例2：输入 s = \"catsandog\"，wordDict = [\"cats\", \"dog\", \"sand\", \"and\", \"cat\"]，输出为 false。
    • 无法找到满足条件的拆分方式。

 题目程序：

#include  // 标准输入输出头文件#include  // 标准库头文件，包含动态内存分配函数#include  // 字符串处理头文件// 主功能函数：判断字符串s是否能拆分为字典中的单词int wordBreak(char* s, char** wordDict, int wordDictSize) { int n = strlen(s); // 获取输入字符串s的长度 // 动态分配并初始化dp数组（长度n+1），dp[i]表示前i个字符是否能拆分 int* dp = (int*)calloc(n + 1, sizeof(int)); // 使用calloc初始化为0 dp[0] = 1; // 空字符串视为可拆分（true） // 外层循环：遍历字符串的每个位置（1到n） for (int i = 1; i <= n; i++) { // 内层循环：遍历字典中的每个单词 for (int j = 0; j =单词长度 2.拆分点之前的子串可拆分 3.当前子串匹配单词 if (i >= len && dp[i - len]) { // 比较s[i-len]到s[i-1]的子串是否等于当前单词 if (strncmp(s + i - len, word, len) == 0) {  dp[i] = 1; // 满足条件则标记当前位置可拆分  break; // 找到匹配后跳出内层循环，提高效率 } } } } int result = dp[n]; // 保存最终结果（整个字符串是否可拆分） free(dp);  // 释放动态分配的dp数组 return result; // 返回最终结果}// 测试函数int main() { // 测试用例1：s=\"applepenapple\", wordDict=[\"apple\",\"pen\"] char* s1 = \"applepenapple\"; char* dict1[] = {\"apple\", \"pen\"}; int size1 = 2; printf(\"Test2: %d\\n\", wordBreak(s1, dict1, size1)); // 应输出1(true) // 测试用例2：s=\"catsandog\", wordDict=[\"cats\",\"dog\",\"sand\",\"and\",\"cat\"] char* s2 = \"catsandog\"; char* dict2[] = {\"cats\", \"dog\", \"sand\", \"and\", \"cat\"}; int size2 = 5; printf(\"Test3: %d\\n\", wordBreak(s2, dict2, size2)); // 应输出0(false) return 0; // 程序正常退出}

输出结果：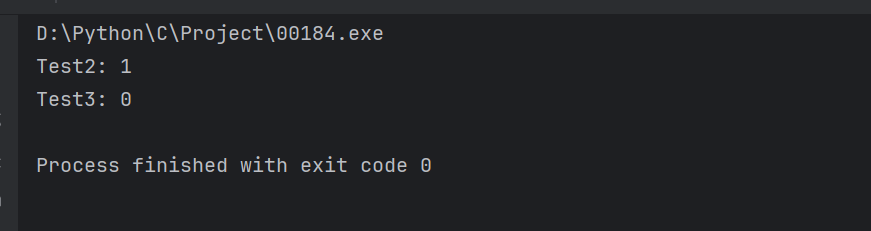

问题二：最大黑方阵——边界条件的拓扑博弈
给定一个整数数组 nums，每次操作中选择一个数，删除它并获得它的点数，同时删除所有等于它的前一个和后一个数。目标是找到可以获得的最大点数。例如，输入 nums = [3,4,2]，输出为6，因为删除4得到4点数，同时删除3，然后删除2得到2点数，总点数6。

🔍 问题本质
在二值方阵（0=黑，1=白）中，寻找四条边全黑的最大子方阵。输出左上角 (r,c)(r,c) 和边长 sizesize。

⚙️ 算法核心：预处理的边界艺术

预处理：连续黑像素矩阵

  • 构建两个辅助矩阵：

    • right[i][j]：从 (i,j)(i,j) 向右的连续黑像素数。

    • down[i][j]：从 (i,j)(i,j) 向下的连续黑像素数。

  • 逆向枚举 + 边界验证

    • Step 1: 从大到小枚举边长 ss（从 min⁡(N,M)min(N,M) 递减到 1）。

    • Step 2: 对每个 ss，枚举左上角 (r,c)(r,c)：

      • 验证四条边：

        • 上边：从 (r,c)(r,c) 向右需 ≥s≥s 个黑像素 → 检查 right[r][c]≥sright[r][c]≥s。

        • 下边：从 (r+s−1,c)(r+s−1,c) 向右需 ≥s≥s 个黑像素 → 检查 right[r+s−1][c]≥sright[r+s−1][c]≥s。

        • 左边：从 (r,c)(r,c) 向下需 ≥s≥s 个黑像素 → 检查 down[r][c]≥sdown[r][c]≥s。

        • 右边：从 (r,c+s−1)(r,c+s−1) 向下需 ≥s≥s 个黑像素 → 检查 down[r][c+s−1]≥sdown[r][c+s−1]≥s。

      • 若满足，返回 [r,c,s][r,c,s]（按题目要求选择最小 r,cr,c）。

  • 时空复杂度

    • 时间：O(N3)O(N3)（枚举边长 O(N)O(N) × 枚举位置 O(N2)O(N2)）。

    • 空间：O(N2)O(N2)（存储 right 和 down 矩阵）。

  • 🎯 关键洞见

    边界拓扑学：将“四条边全黑”的条件拆解为四个边界点的连续性验证。预处理矩阵如同绘制像素流向地图，使边界检查降至 O(1)O(1) 时间。

详细分析：

频率统计：统计每个数值在数组中的出现次数，并计算每个数值的总点数（数值 × 次数）。

动态规划：定义一个数组 dp，其中 dp[i] 表示处理到数值 i 时的最大点数。

状态转移：dp[i] = max(dp[i-1], dp[i-2] + points[i])。

验证示例：

示例1：输入 nums = [3,4,2]，输出为6。

删除4，获得4点数，同时删除3。

删除2，获得2点数，总点数为6。

示例2：输入 nums = [2,2,3,3,3,4]，输出为9。

删除3，获得3 × 3 = 9点数，同时删除2和4。

总点数为9。 

结果计算：dp[max_num] 即为最大点数。

题目程序：

#include  // 标准输入输出头文件#include  // 标准库头文件，包含动态内存分配函数#include  // 字符串处理头文件// 辅助函数：返回两个整数中的较大值int max(int a, int b) { return a > b ? a : b; // 三元运算符实现比较}// 主功能函数：计算可获得的最大点数int deleteAndEarn(int* nums, int numsSize) { if (numsSize == 0) return 0; // 空数组直接返回0 // 步骤1：找出数组中的最大值 int max_num = 0; // 初始化最大值为0 for (int i = 0; i  max_num) { max_num = nums[i]; // 更新最大值 } } // 步骤2：创建并初始化点数数组（长度max_num+1） int* points = (int*)calloc(max_num + 1, sizeof(int)); // 使用calloc初始化为0 // 统计每个数字的点数（数值×出现次数） for (int i = 0; i = 1) { dp[1] = max(points[0], points[1]); // 数字0和1的最大值 } // 动态规划状态转移 for (int i = 2; i <= max_num; i++) { // 状态转移方程：dp[i] = max(不选当前数字, 选当前数字) dp[i] = max(dp[i - 1], dp[i - 2] + points[i]); } int result = dp[max_num]; // 保存最终结果 // 步骤4：释放动态分配的内存 free(points); // 释放点数数组 free(dp); // 释放dp数组 return result; // 返回最大点数}// 测试函数int main() { // 测试用例1：nums = [3,4,2] 预期结果:6 int nums1[] = {3, 4, 2}; int size1 = sizeof(nums1) / sizeof(nums1[0]); printf(\"Test1: %d\\n\", deleteAndEarn(nums1, size1)); // 应输出6 // 测试用例2：nums = [2,2,3,3,3,4] 预期结果:9 int nums2[] = {2, 2, 3, 3, 3, 4}; int size2 = sizeof(nums2) / sizeof(nums2[0]); printf(\"Test2: %d\\n\", deleteAndEarn(nums2, size2)); // 应输出9 // 测试用例3：nums = [1,1,1,2,4,5,5,5,6] 预期结果:18 int nums3[] = {1, 1, 1, 2, 4, 5, 5, 5, 6}; int size3 = sizeof(nums3) / sizeof(nums3[0]); printf(\"Test3: %d\\n\", deleteAndEarn(nums3, size3)); // 应输出18 return 0; // 程序正常退出}

输出结果：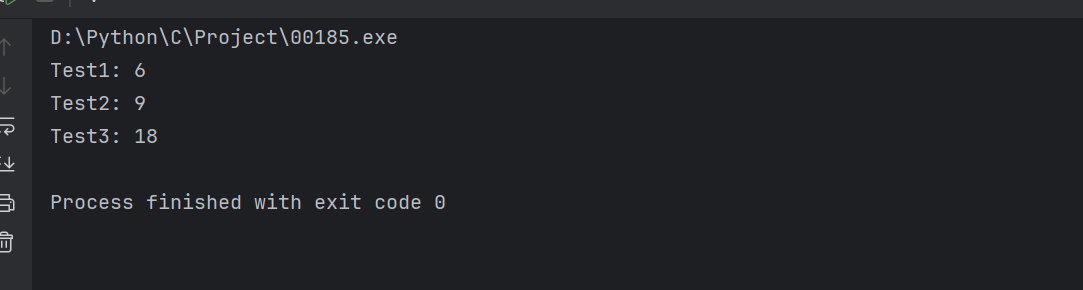 

算法对比：数据压缩 VS 边界拓扑

下表揭示二者本质差异：

维度 最大子矩阵 最大黑方阵 目标 最大化内部元素和 满足边界条件（四边全黑） 输入特性 任意整数（正/负/零） 二值矩阵（0或1） 输出形式 矩形 [r1,c1,r2,c2][r1,c1,r2,c2] 方阵 [r,c,size][r,c,size] 核心策略 降维（行压缩 + Kadane算法） 预处理（连续像素映射） 时间复杂度 O(N2M)O(N2M) O(N3)O(N3) 空间复杂度 O(M)O(M) O(N2)O(N2) 关键操作 行求和 + 一维动态规划 边界连续性验证 适用场景 金融数据热点检测 图像边框识别 哲学隐喻 黑洞模型（吸收最大能量） 城堡模型（守卫森严的边界）
思维升华：算法设计的二元论

  1. 时空权衡的辩证法

    • 最大子矩阵：牺牲时间（O(N2M)O(N2M)）换取空间效率（O(M)O(M)）。

    • 最大黑方阵：牺牲空间（O(N2)O(N2)）换取验证效率（O(1)O(1) 边界检查）。

  2. 问题转化的艺术

    • 子矩阵：通过行压缩将二维问题化为一维动态规划，体现分治思想。

    • 黑方阵：通过连续性预处理将几何约束转为查表操作，体现预计算智慧。

  3. 应用场景启示

    • 最大子矩阵：适用于数值型数据挖掘（如股票收益热区分析）。

    • 最大黑方阵：适用于二值图像处理（如二维码边框检测）。

终极洞见：矩阵是数据的战场，算法是指挥的艺术。最大子矩阵是“集中优势兵力攻其一点”，最大黑方阵是“严守边关拒敌门外”。

博客结语

穿过矩阵迷宫的双子星，我们目睹了算法设计的极致美学：一个用降维打击撕裂高维混沌，一个用边界拓扑编织完美牢笼。它们的对决没有胜负——唯有在问题宇宙中的交相辉映。当你下次面对矩阵时，请记住：

所有复杂问题，皆可拆解为简单世界的投影；所有边界约束，皆是拓扑流动的凝固瞬间。

明日探险预告：《图论中的暗物质：最大流与最小割的量子纠缠》——我们不见不散！

网络标签：

相关问题