动态规划问题 -- 路径模型第一题（不同路径）

目录

• 动态规划分析问题五步曲
• 路径模型常用的分析方法（经验）
• 题目概述
• 代码编写
• 路径模型题单（后续会一一讲解）

动态规划分析问题五步曲

不清楚动态规划分析问题是哪关键的五步的少年们可以移步到
链接: 动态规划算法基础
这篇文章非常详细的介绍了动态规划算法是如何分析和解决问题的

路径模型常用的分析方法（经验）

路径模型的问题通常会给出一个网格（所以我们的dp表应该开为二维的），我们通常的做法是选择网格中的一个位置然后分析网格周围的元素得出状态表示和状态转移方程

题目概述

链接: 不同路径

1. 状态表示（题目要求+自己的经验）
   本题状态dp[i][j] ：表示到第i位置j位置一共有多少路径

2. 状态转移方程推导
   找到网格中一个位置，分析身边元素的状态
   得出状态转移方程式 dp[i][j] = dp[i-1][j] + dp[i][j-1]
   

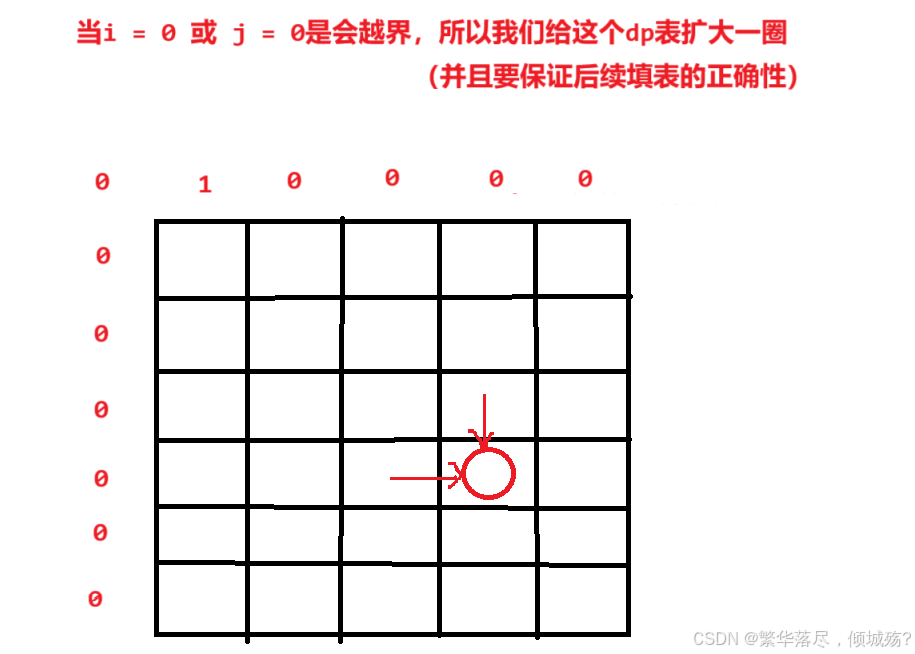
3. 初始化（防止越界+结合状态表示初始化）
   dp表的行和列都扩一个位置，令新dp[0][1] = 1
   

4. 填表顺序（分析要填i位置前一个依赖状态的位置）
   dp[i][j] = dp[i-1][j] + dp[i][j-1] , 显然是从上到下，从左到右填表

5. 返回值（由题目要求来）
   返回dp[m][n];

代码编写

分析了动态规划五步曲后就可以写出优雅的代码了

 int uniquePaths(int m, int n) { if(m == 1 && n == 1) return 1; vector<vector<int>> dp(m+1,vector<int>(n+1)); dp[0][1] = 1; for(int i = 1 ; i <= m ; i++) for(int j = 1 ; j <= n ; j++) dp[i][j] = dp[i-1][j] + dp[i][j-1]; return dp[m][n]; } 

路径模型题单（后续会一一讲解）

链接: 不同路径II
链接: 珠宝的最高价值
链接: 下降路径最小和
链接: 最小路径和

少年今天的你又进步了一点点唷，明天继续加油吧