网站导航
> 技术文档 > 【A题解题思路】2025电工杯数学建模A题解题思路+可运行代码参考（无偿分享）_问题1:基于历史功率的光伏电站发电特性分析 基于光伏电站的地理位置信息,结合太阳

【A题解题思路】2025电工杯数学建模A题解题思路+可运行代码参考（无偿分享）_问题1:基于历史功率的光伏电站发电特性分析 基于光伏电站的地理位置信息,结合太阳

网友: 技术文档 2025-07-30 13:54:00

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

A 题 光伏电站发电功率日前预测问题

问题1 基于历史功率的光伏电站发电特性分析

基于光伏电站的地理位置信息，结合太阳辐照计算理论可发功率，研究其长周期（季节性变化）和短周期（日内波动）特性。根据实际功率与理论可发功率的偏差，分析光伏电站发电功率特性。

问题 1 分析

本问题要求基于地理位置和日期信息，构建一个不依赖天气预报的光伏电站理论可发功率模型，并结合实际功率数据分析其长期与短期变化特征。题目本质是构造一个太阳辐射驱动的物理模型，用于估计在理想光照下的发电上限。适合采用太阳位置几何模型与能量转换公式进行建模，通过计算赤纬角、时角、太阳高度角推导辐照强度，并结合转换效率得出理论功率，再与实际功率对比提取日内周期性与季节趋势，为后续预测模型提供物理先验支撑。

解题思路：

一、理论功率模型构建（太阳辐射建模）

1. 太阳位置计算模型（SPA简化版）

光伏发电的功率本质上由单位面积接收到的太阳辐照强度决定，而辐照强度与太阳高度角密切相关。设：

  • ϕ：光伏电站纬度
  • n：一年中的第 n 天
  • H：时角（即一天中某时相对正午的太阳位置）
  • δ：太阳赤纬角，表示太阳相对于赤道的位置

则太阳赤纬角为：

\\delta = 23.45^\\circ \\cdot \\sin\\left( \\frac{360^\\circ}{365} \\cdot (n - 81) \\right)

太阳高度角 α 表示太阳光与地平面的夹角，计算如下：

       \\alpha =\\arcsin (\\sin \\phi \\cdot \\sin \\delta +\\cos \\phi \\cdot \\cos \\delta \\cdot \\cos H)

其中，时角 H 的单位为度：

H={​{15}^{​{}^\\circ }}\\cdot ({​{t}_{solar}}-12)

表示当前时刻与正午的偏移量（单位小时）。

2. 辐照强度与理论功率

基于 α估算地面单位面积接受的太阳辐照强度：

G(t)={​{G}_{sc}}\\cdot {​{E}_{0}}\\cdot \\sin \\alpha

其中：

  • {​{G}_{sc}}=1367\\text{W/}{​{\\text{m}}^{2}}：太阳常数
  • {​{E}_{0}}=1+0.033\\cdot \\cos \\left( \\frac{​{​{360}^{​{}^\\circ }}n}{365} \\right)：地球轨道偏心校正因子

理论可发功率（假设面板总面积 A、效率 η）为：

                                     {​{P}_{th}}(t)=\\eta \\cdot A\\cdot G(t)

注意：如果考虑倾角 θ，需将入射角影响加入：

{G}\'(t)=G(t)\\cdot \\cos (\\theta -\\alpha )

二、实际功率特征提取

1. 长周期（季节性）变化分析

  • 平均功率趋势可用滑动平均计算：

P_{\\text{avg}}(t) = \\frac{1}{w} \\sum_{i=t-w/2}^{t+w/2} P_{act}(i)

  • 傅里叶变换用于提取周期成分：

F(k) = \\sum_{t=1}^{N} P_{act}(t) \\cdot e^{-2\\pi i k t / N}

其频谱幅值峰值可对应年周期、月周期等成分。

2. 短周期（日内波动）模式分析

将所有日内功率数据按 15min 间隔分为 96 段，计算平均日内曲线：

\\bar{P}{day}(j) = \\frac{1}{M} \\sum{d=1}^{M} P_{act}^{(d)}(j), \\quad j = 1, ..., 96

其中：

  • M：样本天数
  • j=1,2,...,96：每天的时间段编号

可用热图展示不同季节的日内曲线分布，揭示发电开始/结束时段与峰值。

三、理论-实际偏差分析与优化拟合

我们定义偏差率函数：

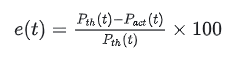
存在系统性偏差的原因包括：

  • 模型中效率 η与实际不同
  • 季节性遮挡、空气质量、温度抑制效应
  • 实际运行状况（如面板污染、电网限制等）

四、引入粒子群算法（PSO）进行拟合优化

为拟合实际数据，我们引入智能优化算法 PSO（Particle Swarm Optimization）对关键参数（例如\\eta、A、k(t)）进行全局优化，目标是使理论功率曲线尽可能逼近历史真实功率。

1. PSO目标函数设定：

定义优化目标为最小化预测与真实功率差的平方和：

\\min_{\\eta, k(t)} \\sum_t \\left( \\eta \\cdot A \\cdot k(t) \\cdot G(t) - P_{act}(t) \\right)^2

其中：

  • k(t)：动态折减因子，表示天气环境影响
  • \\eta ：待拟合的转换效率

2. 粒子群优化流程：

  • 初始化粒子：每个粒子表示一个参数组合 (\\eta_i, A_i, \\{k_i(t)\\})
  • 计算适应度：每个粒子的适应度为目标函数值
  • 更新速度与位置：
  • 速度更新：

v_i(t+1) = w \\cdot v_i(t) + c_1 r_1 (p_i - x_i(t)) + c_2 r_2 (g - x_i(t))

  • 位置更新：

x_i(t+1) = x_i(t) + v_i(t+1)

其中：

  • w：惯性权重
  • c_1, c_2：个体和全局学习因子
  • r_1, r_2：0~1 的随机数
  • p_i：粒子个体最优位置
  • g：全局最优位置
  • 迭代至收敛或达到最大代数

该过程可自动寻找最优\\eta、A、k(t)，从而解释理论-实际差异，并反推环境影响。

Python代码： 

import numpy as npimport pandas as pdimport matplotlib.pyplot as plt# 参数设定phi = np.radians(34.0) # 纬度eta = 0.18  # 面板效率A = 1000 # 面板面积 (m^2)G_sc = 1367 # 太阳常数 W/m^2# 计算太阳赤纬角def solar_declination(n): return np.radians(23.45 * np.sin(2 * np.pi * (n - 81) / 365))# 时角（小时 -> 弧度）def hour_angle(hour): return np.radians(15 * (hour - 12))# 轨道修正系数def e0_factor(n): return 1 + 0.033 * np.cos(2 * np.pi * n / 365)# 高度角def solar_altitude(phi, delta, H): return np.arcsin(np.sin(phi) * np.sin(delta) + np.cos(phi) * np.cos(delta) * np.cos(H))# 理论功率def theoretical_power(n, hours): delta = solar_declination(n) E0 = e0_factor(n) H = hour_angle(hours) alpha = solar_altitude(phi, delta, H) G = G_sc * E0 * np.sin(alpha) G[G < 0] = 0 return eta * A * G# 生成一天的96个时点（15分钟间隔）hours = np.linspace(0, 24, 96, endpoint=False)# 示例第52天理论功率P_th = theoretical_power(52, hours)# 生成示例实际功率（带有噪声与削弱效应）np.random.seed(42)P_act = P_th * (0.8 + 0.2 * np.random.rand(len(P_th)))# 计算偏差error = (P_th - P_act) / (P_th + 1e-6) * 100error[P_th == 0] = 0 # 避免除0# 可视化plt.figure(figsize=(10, 6))plt.subplot(2,1,1)plt.plot(hours, P_th, label=\'理论功率\')plt.plot(hours, P_act, label=\'实际功率\', linestyle=\'--\')plt.title(\'理论与实际功率对比\')plt.xlabel(\'时间（小时）\')plt.ylabel(\'功率（W）\')plt.legend()plt.grid(True)plt.subplot(2,1,2)plt.plot(hours, error, color=\'red\')plt.title(\'相对误差（%）\')plt.xlabel(\'时间（小时）\')plt.ylabel(\'误差 %\')plt.grid(True)plt.tight_layout()plt.savefig(\"q1_theoretical_vs_actual.png\")plt.show()

后续都在“数模加油站”......

网络标签：

相关问题