基础但极其重要且优雅 | 从旋转矩阵的左乘右乘 到 位姿矩阵左乘右乘的物理意义(保姆级教学)_旋转矩阵左乘和右乘的区别
文章目录
- 前言
- 一、基础旋转矩阵的两种定义
-
- 坐标系的旋转(被动旋转)
- 向量的旋转(主动旋转)
- SLAM中使用的旋转矩阵
-
- GPT解释
- 笔者理解
- 二、旋转矩阵中左乘与右乘的本质区别
-
- 定义
- 左乘原理 - 向量绕固定坐标系旋转
- 右乘原理 - 绕自身坐标系的坐标变换
- 三、相机位姿矩阵 T c w T_{cw} Tcw 和 T w c T_{wc} Twc
-
- 定义
- 解释
- T c w T_{cw} Tcw 和 T w c T_{wc} Twc 两者之间的关系
- 回答前言问题
- 四、SLAM中的位姿移动计算
-
- 连续位姿移动使用左乘
- Δ T i \\Delta T_i ΔTi的物理意义
- 同一次 Δ T \\Delta T ΔT在两种系下的关系
- 五、固定的点或位姿在坐标变换中的矩阵运算
-
- 矛盾
- 从固定点开始推导,为什么使用了右乘进行运算
- 从固定位姿开始推导,需要注意的地方
- 六、 自动驾驶中的IMU姿态更新
-
- IMU的姿态
- IMU给出数据的方式
- 为什么与定义不一致
- 坐标系本身变换,使用左乘/右乘的解释
- 为什么IMU角度推算应该用右乘
- 《自动驾驶...SLAM...》2.2.1 论述不严谨的地方
-
- 右乘IMU系下角速度证明
- 左乘全局系下角速度证明
- 感想
前言
在矩阵运算中,左乘与右乘 是两个看似简单但至关重要的概念。对于刚接触SLAM或自动驾驶的初学者而言,这个区别可能并不明显,因为它往往并不影响对整体概念的理解,比如SLAM流程、松紧耦合等。然而,当一名技术人员真正开始开发项目、推导公式时,何时使用左乘,何时使用右乘 将直接影响计算的正确性与逻辑的严谨性。
笔者查阅了大多CSDN上面的文章,觉得在SLAM或自动驾驶的方向,缺少一个关于左乘和右乘的总结,并且这个问题也困扰了我一段时间。因此在理清后,认为有必要在这里做一个阐述,如果有不明确的地方欢迎大家指正!
如果你希望检验自己是否真正理解了这个知识点,不妨思考以下几个关键问题:
-
最纯粹的旋转矩阵的两种定义方式有哪些?SLAM中用的是哪一种?
-
旋转矩阵中,左乘与右乘的本质区别是什么?
-
相机位姿矩阵 T c w T_{cw} Tcw 和 T w c T_{wc} Twc 各自代表什么?
除了物理意义上表示坐标系之间的变换,它们的数学意义究竟是什么?换句话说,如果我们使用 T w c T_{wc} Twc 作为相机的位姿,那么初始时刻世界坐标系与相机坐标系重合。假设相机系围绕世界系的 Z Z Z 轴逆时针旋转30度,并沿世界系的 X X X 轴和 Y Y Y 轴分别平移 +1 和 +2,构造出 4×4 变换矩阵 T T T 后,如何计算相机系下的固定点 P cP_c Pc 在世界坐标系下的坐标 P wP_w Pw? -
SLAM中的位姿移动计算:左乘还是右乘?
在SLAM中,我们经常需要计算从一个时刻的相机位姿到另一个时刻的相机位姿,这通常涉及多个增量变换 Δ T i\\Delta T_i ΔTi。在这种情况下,应该采用连续左乘还是连续右乘?为什么?分别以 T c w T_{cw} Tcw 和 T w c T_{wc} Twc 代表相机位姿,则 Δ T i\\Delta T_i ΔTi代表的物理意义又是什么? -
坐标变换中的矩阵运算:如何正确选择乘法顺序?
SLAM 计算过程中,常常需要将某个固定点或位姿在不同的坐标系中进行连续变换,以得到新的坐标。在这种情况下,应该采用左乘还是右乘?为什么? -
自动驾驶中的IMU姿态更新:旋转矩阵的乘法顺序如何决定?
在自动驾驶中,IMU 用于估计车辆姿态,尤其是旋转的累积。在仅考虑旋转矩阵的情况下,车辆从一个时刻的姿态到另一个时刻的姿态,经历了多个增量旋转矩阵 Δ R i\\Delta R_i ΔRi。此时,应该采用左乘还是右乘?其数学原理和物理意义是什么?
一、基础旋转矩阵的两种定义
坐标系的旋转(被动旋转)
翻阅《捷联惯性导航技术》(第二版),可以发现 3.6.3 欧拉角 章节中,对 参考坐标系 n 旋转到 载体坐标系 b 有如下定义
R ( α ) = [ cos α sin α0 − sin α cos α0 0 0 1 ] \\begin{aligned}\\boldsymbol{R}(\\alpha)=\\left[\\begin{array}{ccc}\\cos \\alpha & \\sin \\alpha & 0 \\\\ -\\sin \\alpha & \\cos \\alpha & 0 \\\\ 0 & 0 & 1\\end{array}\\right]\\end{aligned} R(α)= cosα−sinα0sinαcosα0001
这样定义的理由如下

如上图举个例子,你可以发现它们符合这样的过程,将参考坐标系 n ( x−y x-y x−y) 下的点 转换到 载体坐标系 b ( x ′ − y ′ x\'-y\' x′−y′) 下,即以参考坐标系 n为基准,逆时针旋转30度到了载体坐标系 b。
[ 5 3 + 5 5 3 − 5] = [ cos 30 ∘ sin 30 ∘ − sin 30 ∘ cos 30][ 10 10 ] \\left[\\begin{array}{l}5 \\sqrt{3}+5 \\\\ 5 \\sqrt{3}-5\\end{array}\\right]=\\left[\\begin{array}{cc}\\cos 30^{\\circ} & \\sin 30^{\\circ} \\\\ -\\sin 30^{\\circ} & \\cos 30\\end{array}\\right]\\left[\\begin{array}{c}10\\\\ 10\\end{array}\\right] [53+553−5]=[cos30∘−sin30∘sin30∘cos30][1010]
P b = R b n P n P_b=R_{bn}P_{n} Pb=RbnPn
所以被称为坐标系的旋转
向量的旋转(主动旋转)
如果是向量的旋转,不涉及到坐标系的旋转,定义如下
R ( α ) = [ cos α − sin α0 sin α cos α0 0 0 1 ] \\begin{aligned}\\boldsymbol{R}(\\alpha)=\\left[\\begin{array}{ccc}\\cos \\alpha & -\\sin \\alpha & 0 \\\\ \\sin \\alpha & \\cos \\alpha & 0 \\\\ 0 & 0 & 1\\end{array}\\right]\\end{aligned} R(α)= cosαsinα0−sinαcosα0001
可以用下图的计算来证明

( x ′ y ′ ) = ( cos 30 ∘ − sin 30 ∘ sin 30 ∘ cos 30 ∘ )( 4 2 ) = ( 0.8660254 − 0.5 0.5 0.8660254 )( 4 2 ) \\binom{x^{\\prime}}{y^{\\prime}}=\\left(\\begin{array}{cc} \\cos 30^{\\circ} & -\\sin 30^{\\circ} \\\\ \\sin 30^{\\circ} & \\cos 30^{\\circ} \\end{array}\\right)\\binom{4}{2}=\\left(\\begin{array}{cc} 0.8660254 & -0.5 \\\\ 0.5 & 0.8660254 \\end{array}\\right)\\binom{4}{2} (y′x′)=(cos30∘sin30∘−sin30∘cos30∘)(24)=(0.86602540.5−0.50.8660254)(24)
SLAM中使用的旋转矩阵
SLAM和自动驾驶中使用的统一定义为了 向量的旋转(主动旋转) ,即使是在同一个点在不同坐标系下的转换的时候(因此这里在 右乘原理 - 绕自身坐标系的坐标变换 小结,就会出现反直觉的情况)。

举个例子 绕Z轴,以世界系为基准,相机系相对于世界系逆时针旋转了30度,对应的公式为 P w = R w c P c P_w=R_{wc}P_{c} Pw=RwcPc
对应的旋转矩阵和例子如下,看上去应该是 以世界系为基准,旋转到 相机系。这与我们的被动旋转定义是相反的,被动旋转的情况应该是,以相机系为基准,旋转到世界系。
[ 10 10 ] = [ cos 30 ∘ − sin 30 ∘ sin 30 ∘ cos 30][ 5 3 + 5 5 3 − 5] \\left[\\begin{array}{l}10 \\\\ 10\\end{array}\\right]=\\left[\\begin{array}{cc}\\cos 30^{\\circ} & -\\sin 30^{\\circ} \\\\ \\sin 30^{\\circ} & \\cos 30\\end{array}\\right]\\left[\\begin{array}{c}5 \\sqrt{3}+5 \\\\ 5 \\sqrt{3}-5\\end{array}\\right] [1010]=[cos30∘sin30∘−sin30∘cos30][53+553−5]
为什么要如此定义?
GPT解释
物理动作:确实是在说“相机系绕世界系转了 30°”,这是一个 被动 的描述(坐标系在动)。
我们要做的:把「相机系坐标」→「世界系坐标」,数学上要用到的是 “相机系的基底在世界系里的朝向”,也就是把相机系的轴看成一组在世界系中的矢量,那组矢量恰好是由主动旋转 +30 得到的。
笔者理解
SLAM必会涉及到 平移,那么加上平移以后,会有如下公式,这个时候不如不考虑旋转,只考虑平移,会发现,平移只有以 世界系为基准,指向 相机系的原点,公式才可以成立。
P w = T w c P c P_w=T_{wc}P_{c} Pw=TwcPc

[ 3 3 1 ] = [ 1 0 3 0 1 3 0 0 1 ][ 0 0 1 ] \\left[\\begin{array}{l} 3 \\\\ 3 \\\\ 1 \\end{array}\\right]=\\left[\\begin{array}{lll} 1 & 0 & 3 \\\\ 0 & 1 & 3 \\\\ 0 & 0 & 1 \\end{array}\\right]\\left[\\begin{array}{l} 0 \\\\ 0 \\\\ 1 \\end{array}\\right] 331 = 100010331 001
注意,后面文章的讨论全部是基于SLAM的主动旋转
二、旋转矩阵中左乘与右乘的本质区别
定义
左乘旋转矩阵绕固定坐标系旋转,且这里讨论的是非固定向量的旋转。
右乘旋转矩阵绕自身坐标系旋转,且这里讨论的是固定点的坐标变换。
在后面的讲解中,一定要先分清,到底是在进行固定点的坐标变换,还是在进行非固定向量的旋转,否则非常有误导性
同时给出绕 x,y,z x,y,z x,y,z轴旋转的旋转矩阵的定义
R x ( γ ) = [ 1 0 0 0 cos γ − sin γ 0 sin γ cos γ ] R y ( β ) = [ cos β0 sin β 0 1 0 − sin β0 cos β ] R z ( α ) = [ cos α − sin α0 sin α cos α0 0 0 1 ] \\begin{aligned} & \\boldsymbol{R}_x(\\gamma)=\\left[\\begin{array}{ccc}1 & 0 & 0 \\\\ 0 & \\cos \\gamma & -\\sin \\gamma \\\\ 0 & \\sin \\gamma & \\cos \\gamma\\end{array}\\right] \\\\ & \\boldsymbol{R}_y(\\beta)=\\left[\\begin{array}{ccc}\\cos \\beta & 0 & \\sin \\beta \\\\ 0 & 1 & 0 \\\\ -\\sin \\beta & 0 & \\cos \\beta\\end{array}\\right] \\\\ & \\boldsymbol{R}_z(\\alpha)=\\left[\\begin{array}{ccc}\\cos \\alpha & -\\sin \\alpha & 0 \\\\ \\sin \\alpha & \\cos \\alpha & 0 \\\\ 0 & 0 & 1\\end{array}\\right]\\end{aligned} Rx(γ)= 1000cosγsinγ0−sinγcosγ Ry(β)= cosβ0−sinβ010sinβ0cosβ Rz(α)= cosαsinα0−sinαcosα0001
左乘原理 - 向量绕固定坐标系旋转

如图,坐标系 O−xyz O-x y z O−xyz 不变(固定坐标系或世界坐标系), P P P 向量旋转 α \\alpha α ,得到新的向量 P ′ P\' P′
P ′ = R z ( α ) P P\'=\\boldsymbol{R}_z(\\alpha) P P′=Rz(α)P
如果再进行一次角度为 β \\beta β的旋转,可以获得下面的公式
P ′ ′= R z ( β ) P ′ = R z ( β ) R z ( α ) P P\'\'=\\boldsymbol{R}_z(\\beta)P\'=\\boldsymbol{R}_z(\\beta)\\boldsymbol{R}_z(\\alpha)P P′′=Rz(β)P′=Rz(β)Rz(α)P
由此可以发现,在一个固定坐标系下,如果向量 P P P希望持续进行旋转,则只需要通过旋转矩阵进行左乘即可,这里看出来左乘的原因是 α \\alpha α, β \\beta β 是从右向左写的,因此我们称这样的旋转矩阵乘法为左乘。
所以正如定义中所说,左乘旋转矩阵绕固定坐标系旋转,且是非固定向量的旋转。
注意,这里的左乘和向量 P P P无关,只和旋转矩阵之间的乘法有关。不能因为 R z (α)P \\boldsymbol{R}_z(\\alpha) P Rz(α)P就觉得这是左乘了。
右乘原理 - 绕自身坐标系的坐标变换

如图, P P P 点不变,坐标系 O−xyz O-x y z O−xyz 旋转 α \\alpha α ,得到新的坐标系 O− x ′ y ′ z ′ O-x^{\\prime} y^{\\prime} z^{\\prime} O−x′y′z′ ,在新坐标系下, P P P 点的坐标变为 P ′ P^{\\prime} P′ ,则有:
P = R z ( α ) P ′ P=\\boldsymbol{R}_z(\\alpha) P\' P=Rz(α)P′
同理,因为左乘右乘和点 P ′ P\' P′无关,因此不能看到这里就奇怪怎么还是左乘,矩阵的左乘右乘取决于旋转矩阵之间的乘法。
解释一下这里的绕自身坐标系
- 其实就指的是以 O − x y z O-x y z O−xyz为起始坐标系,绕着这个坐标系进行旋转,很多地方也说是 绕相对坐标系
- 举个例子,图中的 α \\alpha α假设大小为30度,那么就等于将 O − x y z O-x y z O−xyz逆时针旋转了30度。由于是逆时针旋转的,因此带入的 α \\alpha α为 + 30 +30 +30度。则旋转矩阵应该为
R z ( α ) = [ cos 30 ° − sin 30 ° 0 sin 30 ° cos 30 ° 0 0 0 1 ]{R}_z(\\alpha)=\\left[\\begin{array}{ccc}\\cos 30° & -\\sin 30° & 0 \\\\ \\sin 30° & \\cos30° & 0 \\\\ 0 & 0 & 1\\end{array}\\right] Rz(α)= cos30°sin30°0−sin30°cos30°0001 - P P P和 P ′ P\' P′满足上面的转换关系,笔者在这里举了一个例子,假设了一个符合图片的计算
[ 10 10 ] = [ cos 30 ∘ − sin 30 ∘ sin 30 ∘ cos 30 ] [ 5 3 + 5 5 3 − 5 ]\\left[\\begin{array}{l}10 \\\\ 10\\end{array}\\right]=\\left[\\begin{array}{cc}\\cos 30^{\\circ} & -\\sin 30^{\\circ} \\\\ \\sin 30^{\\circ} & \\cos 30\\end{array}\\right]\\left[\\begin{array}{c}5 \\sqrt{3}+5 \\\\ 5 \\sqrt{3}-5\\end{array}\\right] [1010]=[cos30∘sin30∘−sin30∘cos30][53+553−5]
但这里的坐标变换其实有一点反直觉,明明从 O−xyz O-x y z O−xyz为基准开始旋转的,但是却不是从在 O−xyz O-x y z O−xyz坐标系下的 P P P开始乘以旋转矩阵的。这或许也是坐标转换的难点所在吧,因为这个反直觉的地方也是最容易出错的地方
下面来看看为什么说这里是右乘
为了简化,我们并不以绕 x,y,z x,y,z x,y,z轴来表示旋转矩阵,我们直接记不同的坐标系为 0,1,2 0,1,2 0,1,2。
- 以0系为起始坐标系,从0系旋转到1系的旋转矩阵为 R 01 R_{01} R01
- 以1系为起始坐标系,从1系旋转到2系的旋转矩阵为 R 12 R_{12} R12
- 以0系为起始坐标系,从0系旋转到2系的旋转矩阵为 R 02 R_{02} R02
- 点 p p p在坐标系 0 , 1 , 2 0,1,2 0,1,2中的坐标分别为 p 1 p_1 p1, p 2 p_2 p2, p 3 p_3 p3,那么根据刚才的推断,可以得到下面的三个:
p 1 = R 12 p 2 , p 0 = R 01 p 1 , p 1 = R 12 p 2p_1=R_{12}p_2,p_0=R_{01}p_1,p_1=R_{12}p_2 p1=R12p2,p0=R01p1,p1=R12p2 - 化简一下,可以得到
R 02 = R 01 R 12R_{02}=R_{01}R_{12} R02=R01R12
可以看出,为了从0系转到2系,旋转矩阵的乘法顺序是先从0系转到1系,再右乘从1系转到2系。
并且,这里的旋转,根据我们刚才对 R 01 R_{01} R01, R 12 R_{12} R12, R 02 R_{02} R02的定义,可以发现每次都是相对于新的系进行旋转,换句话说就是相对于一个 相对系 进行旋转,但是我们的点的位置从来没有变过。
所以正如定义中所说,右乘旋转矩阵绕自身(相对)坐标系旋转,且这里讨论的是固定点的坐标变换。
这上面的知识来自于 旋转的左乘右乘 和 旋转矩阵及左右乘的意义,看这一篇就够了,感谢两位作者的贡献。但这里并没有涉及到SLAM或自动驾驶中相关的应用,因此有了这篇文章。
三、相机位姿矩阵 T c w T_{cw} Tcw 和 T w c T_{wc} Twc
定义
- T w c T_{wc} Twc 代表了从相机系转到世界系的转换过程
- T w c T_{wc} Twc 同样代表了,相机光心在世界坐标系下的位姿
- T c w T_{cw} Tcw 代表了从世界系转到相机系的转换过程
- T c w T_{cw} Tcw 同样代表了,世界系中心在相机系下的位姿
解释
- T w c T_{wc} Twc 之所以可以代表从相机系转到世界系的转换过程,是因为假设在相机系下有一个固定点 P c P_c Pc,那么这个固定点在世界系下的坐标被 定义 为 P w = T w c P c P_w=T_{wc}P_{c} Pw=TwcPc。
-
注意!这里的定义就非常符合直觉了,因为 T w c T_{wc} Twc恰恰代表着从相机系转到世界系的过程!但这个是人为定义的,就是为了,符合直觉!
-
但是!却不符合数学!!!这么说是因为从数学上来讲, T w c T_{wc} Twc代表着以世界系为初始坐标系, 转到相机系的过程!
-
我知道这里非常绕,但可以通过一个刚才讲过的例子来说明。我们不考虑平移,只考虑旋转,如图中所示, O − x y z O-x y z O−xyz代表世界坐标系, O − x ′ y ′ z ′ O-x\' y\' z\' O−x′y′z′代表相机坐标系,还是那个代数形式。就可以发现,从相机系转到世界系的旋转矩阵,竟然不是以相机系为初始坐标系,而是以世界系为初始坐标系转到了相机坐标系,这真是太神奇了!之所以神奇,就是因为我之前提到的反直觉的地方。而这里反直觉的地方,其实就是第一节讲的使用了主动旋转矩阵的原因。
[ 10 10 ] = [ cos 30 ∘ − sin 30 ∘sin 30 ∘ cos 30 ] [ 5 3 + 5 5 3 − 5 ] \\left[\\begin{array}{l}10 \\\\ 10\\end{array}\\right]=\\left[\\begin{array}{cc}\\cos 30^{\\circ} & -\\sin 30^{\\circ} \\\\ \\sin 30^{\\circ} & \\cos 30\\end{array}\\right]\\left[\\begin{array}{c}5 \\sqrt{3}+5 \\\\ 5 \\sqrt{3}-5\\end{array}\\right] [1010]=[cos30∘sin30∘−sin30∘cos30][53+553−5]

-
加入了平移以后依然是这个道理
-
- T w c T_{wc} Twc 之所以同样代表了相机光心在世界坐标系下的位姿,也是因为上面的数学,因为 T w c T_{wc} Twc 是以世界系为初始坐标系,然后使用在世界系下的转换关系(角度和平移),得到了相机系。换句话说,相机系的位姿其实就是定义在世界系下的。太优雅了!
- T c w T_{cw} Tcw 代表了从世界系转到相机系的转换过程,我就不再解释了,🐷都会,跟上面一样
- T c w T_{cw} Tcw 同样代表了世界系中心在相机系下的位姿,也是同理。这里可以用 相对 的物理思想来思考,就算只有相机在移动,但是在相机眼里,世界在动(不是我疯了,是这个世界疯了)
T c w T_{cw} Tcw 和 T w c T_{wc} Twc 两者之间的关系
自然是互为逆的关系,可以用数学表示成
T c w= ( T w c ) − 1 T_{c w}=\\left(T_{w c}\\right)^{-1} Tcw=(Twc)−1
证明也很好证明,各位可以自己画一个图,我这里帮大家画了一个图(什么叫保姆式服务)

T w c= [ cos 30 ∘ − sin 30 ∘ 0 1 sin 30 ∘ cos 30 ∘ 0 2 0 0 1 0 0 0 0 1 ] T_{wc}=\\left[\\begin{array}{cccl} \\cos 30^{\\circ} & -\\sin 30^{\\circ} & 0 & 1 \\\\ \\sin 30^{\\circ} & \\cos 30^{\\circ} & 0 & 2 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ \\end{array}\\right ] Twc= cos30∘sin30∘00−sin30∘cos30∘0000101201
T c w= [ cos ( − 30 ) ∘ − sin ( − 30 ) ∘ 0 − ( 32 + 1 ) sin ( − 30 ) ∘ cos ( − 30 ) ∘ 0 1 2 − 3 0 0 1 0 0 0 0 1 ] T_{cw}=\\left[\\begin{array}{cccl} \\cos (-30)^{\\circ} & -\\sin (-30)^{\\circ} & 0 & -\\left(\\frac{\\sqrt{3}}{2}+1\\right) \\\\ \\sin (-30)^{\\circ} & \\cos (-30)^{\\circ} & 0 & \\frac{1}{2}-\\sqrt{3} \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ \\end{array}\\right ] Tcw= cos(−30)∘sin(−30)∘00−sin(−30)∘cos(−30)∘000010−(23+1)21−301
从这里看出, T w c T_{wc} Twc从世界系到相机系逆时针旋转了30度,然后沿着世界系进行平移。而 T c w T_{cw} Tcw则恰恰相反,从相机系到世界系顺时针旋转了30度,然后沿着相机系进行平移(图片中的虚线部分),非常优雅~
回答前言问题
如果我们使用 T w c T_{wc} Twc 作为相机的位姿,那么初始时刻世界坐标系与相机坐标系重合。假设相机系围绕世界系的 Z Z Z 轴逆时针旋转30度,并沿世界系的 X X X 轴和 Y Y Y 轴分别平移 +1 和 +2,构造出 4×4 变换矩阵 T T T 后,如何计算相机系下的固定点 P c P_c Pc 在世界坐标系下的坐标 P w P_w Pw?
[ P w ] = [ cos 30 ∘ − sin 30 ∘ 0 1 sin 30 ∘ cos 30 ∘ 0 2 0 0 1 0 0 0 0 1 ][ P c ] \\left[P_{w}\\right]=\\left[\\begin{array}{cccl} \\cos 30^{\\circ} & -\\sin 30^{\\circ} & 0 & 1 \\\\ \\sin 30^{\\circ} & \\cos 30^{\\circ} & 0 & 2 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ \\end{array}\\right ]\\left[P_{c}\\right] [Pw]= cos30∘sin30∘00−sin30∘cos30∘0000101201 [Pc]
四、SLAM中的位姿移动计算
连续位姿移动使用左乘
道理很简单,因为没有涉及到坐标系的变换,只环绕着固定的坐标系进行移动,因此使用左乘。
举个例子,例如 用 T w c T_{wc} Twc来表达位姿,正如前面的叙述,这里相机的姿态是定义在世界系下的,因此在进行连续移动的时候,在不同时刻间的位姿变换也一直都是在世界系下的,因此是环绕着固定的世界系进行移动。
同样,用 T c w T_{cw} Tcw来表达位姿,这里的相机姿态表达了世界系在相机系下的位姿,此时的固定系为相机系,移动系为世界系,此时是环绕着相机系进行移动。
但这个时候相比于第一部分的例子,也有一点特殊,移动的是一个旋转矩阵 T T T,而不是一个向量,但其实本质一样的
T e n d= Δ T t 3Δ T t 2Δ T t 1 T s t a r t T_{end}=\\Delta T_{t_3}\\Delta T_{t_2}\\Delta T_{t_1}T_{start} Tend=ΔTt3ΔTt2ΔTt1Tstart
Δ T i \\Delta T_i ΔTi的物理意义
如果使用 T w c T_{wc} Twc来表达位姿,则认为 Δ T i \\Delta T_i ΔTi是在世界系下的旋转平移描述。
- 注意!这里是左乘,因此不涉及到反直觉的情况,就大胆的左乘即可。
- 举个例子,刚开始相机系和世界系重合,相机姿态自然为单位矩阵。然后在世界系下,相机系先逆时针绕世界系的Z转30度,再顺时针绕世界系的Z转50度,依然不考虑平移,那么相机的位姿在只考虑旋转的时候,最后可以表示为
R w c e n d = R z ( − 50 ) R z ( + 30 ) R w c s t a r t R_{wc_{end}}=\\boldsymbol{R}_z(-50)\\boldsymbol{R}_z(+30)R_{wc_{start}} Rwcend=Rz(−50)Rz(+30)Rwcstart
如果使用 T c w T_{cw} Tcw来表达位姿,则认为 Δ T i \\Delta T_i ΔTi是在相机系下的旋转平移描述,即在相机移动的时候,认为相机系不动,世界系在转。
因此,无论是哪一种 Δ T i \\Delta T_i ΔTi,都可以代表相机的移动情况
同一次 ΔT \\Delta T ΔT在两种系下的关系
现在有一个这样的推导过程:
T w c ′ = Δ T T w c Δ T − 1 T w c ′ = T w c Δ T − 1 = T w c T w c ′ − 1T w c − 1 Δ T − 1 = T w c ′ − 1T c w ′ = T c w Δ T − 1T w c ′ = Δ T T w c \\begin{array}{l} T_{w c}^{\\prime}=\\Delta T T_{w c} \\\\ \\Delta T^{-1} T_{w c}^{\\prime}=T_{w c} \\\\ \\Delta T^{-1}=T_{w c} T_{w c}^{\\prime-1} \\\\ T_{w c}^{-1} \\Delta T^{-1}=T_{w c}^{\\prime-1} \\\\ T_{c w}^{\\prime}=T_{c w} \\Delta T^{-1} \\\\ T_{w c}^{\\prime}=\\Delta T T_{w c} \\end{array} Twc′=ΔTTwcΔT−1Twc′=TwcΔT−1=TwcTwc′−1Twc−1ΔT−1=Twc′−1Tcw′=TcwΔT−1Twc′=ΔTTwc
最后得到:
T w c ′ = Δ T T w cT c w ′ = T c w Δ T − 1 \\begin{array}{c} T_{w c}^{\\prime}=\\Delta T T_{w c} \\\\ T_{c w}^{\\prime}=T_{c w} \\Delta T^{-1} \\end{array} Twc′=ΔTTwcTcw′=TcwΔT−1
这是个神奇的结果,一个使用了左乘,一个使用了右乘,怎么理解呢?
这会是个很有意思的发现,但不是很好理解。最简单的方式是假设只发生了最简单的平移来理解,然后加上旋转则同理。
我们假设 ΔT \\Delta T ΔT为一个单位旋转矩阵加上一个沿X轴+1的矩阵,即只发生了沿X轴的平移。
我们先设定 T w c T_{wc} Twc为相机位姿,这个时候的相机位姿是表达在世界系下的,即全局固定的坐标系是世界系。那么第一个公式的 ΔT \\Delta T ΔT其实就是相机沿着世界系的X轴远离了一个正单位。注意,这是个事实发生的事情,我们只是使用了两个公式来描述这个过程,分别在不同的坐标系下,如图所示

先不看第二公式,你想想,如果一个相机系在世界系下(相机系在世界系的眼里),沿着世界系X远离一个正单位,那么世界系在相机系下(世界系在相机系的眼里),其实就是依然沿着世界系远离一个负单位!
(建议先看第五部分的IMU在相对系下的右乘更好理解下面的话)
再来看第二个公式, T c w T_{cw} Tcw是表达了世界系中心在相机系下的位姿,换句话说,这里的全局固定的系是相机系,而移动系是世界系。并且因为是右乘,是绕着自身系/相对系的一个转换,也就是绕着世界系的一个转换。再加上是一个逆,所以刚好表达了负单位的想法!绝了,完全证明了“世界系在相机系下,其实就是依然沿着世界系远离一个负单位”
五、固定的点或位姿在坐标变换中的矩阵运算
首先一定要和第三点中的位姿移动计算区分开,因为位姿移动计算中全局坐标系是固定的,可以类比于左乘原理 - 向量绕固定坐标系旋转。这里我们讲的是固定点或位姿在不同的坐标系之间的转换关系,应该类比的是右乘原理 - 绕自身坐标系的坐标变换。
矛盾
我们先来看看SLAM中是怎么定义的。现在有一个固定点 Pc Pc Pc在相机c系下,然后我们从相机c系转到车体b系,再从车体b系转到世界w系,最后得到世界w系下的 Pw Pw Pw,推算过程应该如下:
P w = T w b T b c P c P_w=T_{wb}T_{bc}P_{c} Pw=TwbTbcPc
然后我们简化一下,其实就是从0系到1系,1系到2系的过程,求一个0系下的坐标在2系下的坐标,那么推算过程如下:
P 2 = T 21T 10P 0 P_2=T_{21}T_{10}P_{0} P2=T21T10P0
现在问题来了,这一看不是在左乘吗?左乘不应该是向量绕着固定坐标系旋转吗?但明明这里是固定的点在多个自身/相对坐标系之间的转换,很明显应该使用右乘啊,为什么矛盾了?
其实这是一个右乘后再进行公式推导的结果,只是非常多的地方为了方便直接就写了一个结论,让它看起来像是在左乘,真的很无语
从固定点开始推导,为什么使用了右乘进行运算
之前在讲解右乘的时候,我们提到了一个公式,现在可以用起来,这里没有使用平移,但其实就算加上平移变成位姿矩阵,效果完全相同。
并且注意旋转矩阵这里的定义,与SLAM相同,但我们在理解的时候要按照数学的方式去理解,即,谁是起始坐标系,从谁转到了谁!
- 以0系为起始坐标系,从0系旋转到1系的旋转矩阵为 R 01 R_{01} R01
- 以1系为起始坐标系,从1系旋转到2系的旋转矩阵为 R 12 R_{12} R12
- 以0系为起始坐标系,从0系旋转到2系的旋转矩阵为 R 02 R_{02} R02
然后经过推导我们获得了下面的公式
p 1 = R 12p 2 , p 0 = R 01p 1 , p 1 = R 12p 2 p_1=R_{12}p_2,p_0=R_{01}p_1,p_1=R_{12}p_2 p1=R12p2,p0=R01p1,p1=R12p2
R 02 = R 01R 12 R_{02}=R_{01}R_{12} R02=R01R12
加上点的坐标变换以后会变成
P 0 = R 01R 12P 2 P_{0}=R_{01}R_{12}P_2 P0=R01R12P2
正如我们之前讲的那样,这里是右乘,很好!!!现在有意思的地方来了,我们变换一下这个矩阵的样子,变成
R 12 − 1 R 01 − 1 P 0 = P 2 R 21 R 10 P 0 = P 2 \\begin{array}{l} R_{12}^{-1} R_{01}^{-1} P_{0}=P_{2} \\\\ R_{21} R_{10} P_{0}=P_{2} \\end{array} R12−1R01−1P0=P2R21R10P0=P2
是不是非常神奇,在经历了一次变换以后,又变成左乘了!但是本质上其实是从右乘推导过来的!再跟刚才说有矛盾的公式对比一下会发现,其实矛盾的原因是因为矛盾公式是因为直接拿的是推导以后的结果,而不是用的初始定义。
但最根本的原因,其实还是最开始说的,那个反直觉的地方,希望读者们自己感受一下。
从固定位姿开始推导,需要注意的地方
如果是位姿,其实推导过程与点完全相同!再次注意,左乘和右乘只与旋转+平移矩阵有关,但与位姿矩阵无关。就算位姿矩阵和旋转+平移矩阵长得一模一样,数学上也不能一概而论。区别在于,就算是使用右乘,举个例子,在最开始推导的时候不能写成
E r r o r : T 1 = T 2T 12 Error: T_1=T_2T_{12} Error:T1=T2T12
而应该依然是
T 1 = T 12T 2 T_1=T_{12}T_2 T1=T12T2
六、 自动驾驶中的IMU姿态更新
IMU的姿态
IMU的姿态被定义为 T w b T_{wb} Twb(假设IMU系就是车体系方便写作),想想 T w c T_{wc} Twc的定义与他是完全一致的。
那么我再阐述一遍, T w b T_{wb} Twb代表着IMU在世界系下的位姿,并且是以世界系为起始坐标系,转换到IMU系的过程。例如IMU系在世界系下,相对于世界系逆时针转了30度并且沿着世界系的X轴平移一个单位,那么应该这么写:
T w b= [ cos 30 ∘ − sin 30 ∘ 0 1 sin 30 ∘ cos 30 ∘ 0 0 0 0 1 0 0 0 0 1 ] T_{wb}=\\left[\\begin{array}{cccl} \\cos 30^{\\circ} & -\\sin 30^{\\circ} & 0 & 1 \\\\ \\sin 30^{\\circ} & \\cos 30^{\\circ} & 0 & 0 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ \\end{array}\\right ] Twb= cos30∘sin30∘00−sin30∘cos30∘0000101001
IMU给出数据的方式
IMU只会给出,相对于自己坐标系的,角速度和加速度,因此不是给出基于世界坐标系的角速度和加速度。
换句话说,所有旋转平移都不是绕着固定坐标系进行旋转的,因为IMU的姿态一直都在变!因此肯定不能使用左乘!
并且,我们这里也没有进行坐标变换,怎么感觉也不能使用右乘了?
为什么与定义不一致
因为定义的两种情况都有一个共同的情景:他们讨论的是坐标系内,一个点/位姿/向量的情况,而不是坐标系本身的变化。
如果我们只讨论坐标系本身的变化,那么有以下新的两个定义:
- 矩阵左乘表示相对于静坐标系变换,只考虑旋转矩阵不考虑位姿矩阵也就是外旋
- 矩阵右乘表示相对于动坐标系变换,只考虑旋转矩阵不考虑位姿矩阵也就是内旋
坐标系本身变换,使用左乘/右乘的解释
我举了一个例子来更清晰的说明,就不需要复杂的证明过程了,理解最重要。
现在有一个全局世界系,在全局世界系下有一个IMU系,它的位姿被表达为,绕着世界系的Z轴逆时针旋转180度,同时沿各个轴正向平移10个单位长度。他的位姿矩阵如下
T w b= [ cos 180 ∘ − sin 180 ∘ 0 10 sin 180 ∘ cos 180 ∘ 0 10 0 0 1 10 0 0 0 1 ] T_{wb}=\\left[\\begin{array}{cccl} \\cos 180^{\\circ} & -\\sin 180^{\\circ} & 0 & 10\\\\ \\sin 180^{\\circ} & \\cos 180^{\\circ} & 0 & 10 \\\\ 0 & 0 & 1 & 10 \\\\ 0 & 0 & 0 & 1 \\\\ \\end{array}\\right ] Twb= cos180∘sin180∘00−sin180∘cos180∘0000101010101
现在绕X轴逆时针旋转了90度,但是注意!这里具体是绕哪个系我可没有说,先来看看左乘和右乘的结果。我编了一个MATLAB程序来说明,代码如下,你也可以自己跑
%% =======================% 绘制不同坐标系的示例% =======================function plotCoordSystem(R, t, color, name, scale, isDashed, lineWidth) % 绘制三维坐标系 % R: 3x3旋转矩阵 % t: 3x1平移向量 % color: 颜色 % name: 坐标系名称 % scale: 坐标轴长度 % isDashed: 是否使用虚线 (true = \'--\', false = 实线) % lineWidth: 线的粗细 if nargin < 7 lineWidth = 2; % 默认线宽 2 end if nargin < 6 isDashed = false; % 默认使用实线 end if nargin < 5 scale = 1; end % 坐标轴方向 ex = R(:,1); % x 轴方向 ey = R(:,2); % y 轴方向 ez = R(:,3); % z 轴方向 % 计算终点坐标 x_end = t + scale * ex; y_end = t + scale * ey; z_end = t + scale * ez; % 选择线型 if isDashed lineStyle = \'--\'; % 虚线 else lineStyle = \'-\'; % 实线 end hold on; % 用 plot3 绘制坐标轴(支持虚线) plot3([t(1), x_end(1)], [t(2), x_end(2)], [t(3), x_end(3)], ... lineStyle, \'Color\', color, \'LineWidth\', lineWidth); plot3([t(1), y_end(1)], [t(2), y_end(2)], [t(3), y_end(3)], ... lineStyle, \'Color\', color, \'LineWidth\', lineWidth); plot3([t(1), z_end(1)], [t(2), z_end(2)], [t(3), z_end(3)], ... lineStyle, \'Color\', color, \'LineWidth\', lineWidth); % 添加箭头 (quiver3 只画箭头) quiver3(t(1), t(2), t(3), scale*ex(1), scale*ex(2), scale*ex(3), ... \'Color\', color, \'LineWidth\', max(lineWidth, 1), \'MaxHeadSize\', 0.5); quiver3(t(1), t(2), t(3), scale*ey(1), scale*ey(2), scale*ey(3), ... \'Color\', color, \'LineWidth\', max(lineWidth, 1), \'MaxHeadSize\', 0.5); quiver3(t(1), t(2), t(3), scale*ez(1), scale*ez(2), scale*ez(3), ... \'Color\', color, \'LineWidth\', max(lineWidth, 1), \'MaxHeadSize\', 0.5); % 在坐标系原点附近显示文字 if nargin >= 4 && ~isempty(name) text(t(1), t(2), t(3), [\' \' name], \'Color\', color, \'FontSize\', 12); endend%% ============== 主脚本 ==============clear; clc; close all;% 定义全局坐标系Rg = eye(3);tg = [0; 0; 0];% 定义原始局部坐标系 (Local)Rz180 = [ -1, 0, 0; 0, -1, 0; 0, 0, 1 ]; % 绕Z轴180度tl = [10; 10; 10];% 计算局部坐标系Rx90 = [ 1, 0, 0; 0, 0, -1; 0, 1, 0 ];R_local = Rz180; % 原始局部坐标系R_local2 = Rx90 * R_local;R_local3 = R_local * Rx90;% 画图figure(\'Name\',\'不同坐标系可视化\',\'NumberTitle\',\'off\');set(gcf, \'color\', \'white\');% (1) 绘制全局坐标系 (黑色, 实线, 线宽 2)plotCoordSystem(Rg, tg, \'k\', \'Global\', 3, false, 2);% (2) 绘制原始局部坐标系 (红色, 实线, 线宽 2)plotCoordSystem(R_local, tl, \'r\', \'Local\', 3, false, 2);% (3) 绘制局部坐标系2 (绿色, 虚线, 线宽 1)plotCoordSystem(R_local2, tl, \'g\', \'Local2\', 3, true, 1);% (4) 绘制局部坐标系3 (蓝色, 虚线, 线宽 1)plotCoordSystem(R_local3, tl, \'b\', \'Local3\', 3, true, 1);% 视图设置axis equal; grid on;xlabel(\'X\'); ylabel(\'Y\'); zlabel(\'Z\');title(\'原始局部坐标系 & 左乘 / 右乘绕 X 轴旋转后的坐标系\');view(3); % 3D 视角结果如下
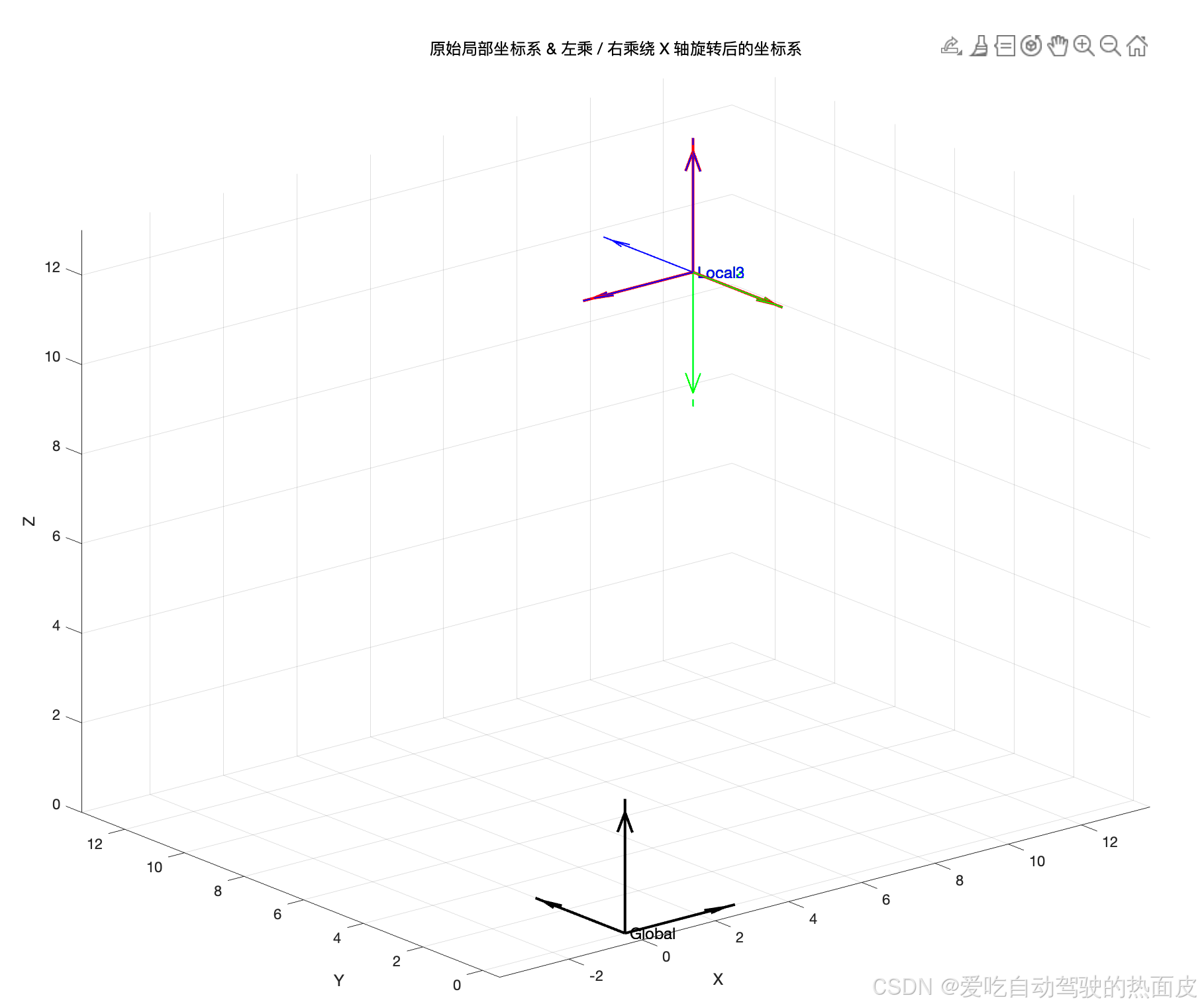
然后对图片做一个说明
- 黑色的是全局坐标系,红色的是局部坐标系
- 绿色的是局部坐标系左乘的结果,你会发现它绕着全局坐标系的X轴逆向旋转了180度
- 蓝色的是局部坐标系右乘的结果,你会发现它绕着局部坐标系的X轴逆向旋转了180度
再来看看概念是不是立刻就懂了
- 矩阵左乘表示相对于静坐标系变换
- 矩阵右乘表示相对于动坐标系变换
这里的相对于静坐标系就是指的全局坐标系,其实这里的变换和第三部分SLAM中的位姿移动计算意义是一样的,比如在 T w c T_{wc} Twc中,如果你把相机姿态当成局部坐标系,那么在全局坐标系里的连续变换的确就是使用连续左乘。当然你也可以吧相机姿态就认为是一个相机姿态,类似于一个向量,那么在全局坐标系里的连续变换的确还是使用连续左乘。
这里的相对于动坐标系就是一个全新的概念了,它不属于第四部分中对右乘的推导,因为没有固定的点或位姿。
仔细来看,相对于动坐标系,我们也可以叫做相对于 相对/局部坐标系,其实就是红色的坐标系。如果相对于红色坐标系进行旋转,那么就是右乘。
为什么IMU角度推算应该用右乘
看到这里应该很清楚了,IMU给出的角速度和加速度都是在IMU系下的,IMU系自己就需要进行旋转,而不需要再在IMU系里找一个一个点/位姿/向量,并且定义IMU的姿态也是使用 T w b T_{wb} Twb,即全局系是世界系,局部系是IMU系。因此IMU给出一个旋转平移的结果 ΔT \\Delta T ΔT也是在IMU系下的,因此使用右乘变换坐标系,并且对应了图片中的蓝色右乘结果!
数学意义就是绕着相对坐标系的一个坐标系旋转,物理意义就是绕着IMU系自己的旋转!
相关的例子你也可以找到,在《自动驾驶与机器人中的SLAM技术从理论到实践中》第2.3节“运动学演示案例:圆周运动”中你就可以找到右乘的使用!但这里完全没有说为什么是右乘,初学者也不会注意这个细节。
《自动驾驶…SLAM…》2.2.1 论述不严谨的地方
在对下面两个的公式的解释中,书上的原话是 这两式没有本质意义上的区别,只是形式不同
R ˙ = R ω ∧ \\dot{\\boldsymbol{R}}=\\boldsymbol{R} \\omega^{\\wedge} R˙=Rω∧ R ˙ = ω ∧ R \\dot{\\boldsymbol{R}}= \\omega^{\\wedge}\\boldsymbol{R} R˙=ω∧R
但其实这里是不严谨的,更严谨的表达如下:
- R R R 代表着 R w b R_{wb} Rwb,与前面小节的解释一致
- 右乘角速度的反对称矩阵,代表着这里的角速度是在IMU系下,对角速度的表达
- 左乘角速度的反对称矩阵,代表着这里的角速度是在全局系下,对角速度的表达
因此后面才使用第一个式子进行丝滑推导,否则如果用第二个式子的话,推导的物理意义就错了,因为IMU无法直接给出在全局系下的三轴角速度,加速度。
证明过程感谢 旋转矩阵求导出现角速度的理解 文章中对这里的详细叙述!真的是说的比唱的还好听,直击灵魂的证明,下面展示最核心的证明过程
右乘IMU系下角速度证明
考虑全局坐标系下旋转角标为S(其实就是世界坐标系),连体坐标系旋转角标为B(其实就是IMU坐标系),空间中一个矢量为u,R 代表着 R w b R_{wb} Rwb,我们有下面的关系:
u S = R u B \\mathbf{u}_{S}=\\mathbf{R} \\mathbf{u}_{B} uS=RuB
求导我们可以得到:
v S = ( d d t R )u B \\mathbf{v}_{S}=\\left(\\frac{\\mathrm{d}}{\\mathrm{~d} t} \\mathbf{R}\\right) \\mathbf{u}_{B} vS=( dtdR)uB
上式中 v s v_{s} vs是全局坐标系下的速度,等式右边没有 u B u_{B} uB的导数是因为连体坐标系内观察坐标始终没有变化,导数为0。
于是我们有:
v S = ω × u S = ω × R u B \\begin{aligned} \\mathbf{v}_{S} & =\\omega \\times \\mathbf{u}_{S} \\\\ & =\\omega \\times \\mathbf{R} \\mathbf{u}_{B} \\end{aligned} vS=ω×uS=ω×RuB
对比我们可以知道:
d d t R = ω × R = [ ω ] × R \\begin{aligned} \\frac{\\mathrm{d}}{\\mathrm{~d} t} \\mathbf{R} & =\\omega \\times \\mathbf{R} \\\\ & =[\\omega]_{\\times} \\mathbf{R} \\end{aligned} dtdR=ω×R=[ω]×R
左乘全局系下角速度证明
我们经常在论文里看到反过来写的旋转矩阵的导数,这又是为什么呢?
d d tR = R [ ω ] × \\frac{\\mathrm{d}}{\\mathrm{~d} t} \\mathbf{R}=\\mathbf{R}[\\omega]_{\\times} dtdR=R[ω]×
准确地说,上述 [ω ] × [\\omega]_{\\times} [ω]×应该指的是物体角速度 [ ω B ] × \\left[\\omega^{B}\\right]_{\\times} [ωB]×:
d d tR = R [ ω B ] × \\frac{\\mathrm{d}}{\\mathrm{~d} t} \\mathbf{R}=\\mathbf{R}\\left[\\omega^{B}\\right]_{\\times} dtdR=R[ωB]×
我们需要搞清楚的是前面所推导和论证的公式准确地说应该描述的是惯性坐标系的空间角速度 [ ω S ] × \\left[\\omega^{S}\\right]_{\\times} [ωS]×:
d d tR = [ ω S ] × R \\frac{\\mathrm{d}}{\\mathrm{~d} t} \\mathbf{R}=\\left[\\omega^{S}\\right]_{\\times} \\mathbf{R} dtdR=[ωS]×R
下面开始证明:
推导一下物体角速度,根据坐标变换关系我们有:
v S = R v B ω S = R ω B \\begin{array}{l} \\mathbf{v}_{S}=\\mathbf{R} \\mathbf{v}_{B}\\\\ \\omega_{S}=\\mathbf{R} \\omega_{B} \\end{array} vS=RvBωS=RωB
根据前面的:
v S = R ˙u B \\mathbf{v}_{S}=\\dot{\\mathbf{R}} \\mathbf{u}_{B} vS=R˙uB
则有:
R − 1 v S = R − 1 R ˙u B \\mathbf{R}^{-1} \\mathbf{v}_{S}=\\mathbf{R}^{-1} \\dot{\\mathbf{R}} \\mathbf{u}_{B} R−1vS=R−1R˙uB
也即:
v B = R − 1 R ˙u B = [ ω B ] ×u B \\mathbf{v}_{B}=\\mathbf{R}^{-1} \\dot{\\mathbf{R}} \\mathbf{u}_{B}=\\left[\\omega^{B}\\right]_{\\times} \\mathbf{u}_{B} vB=R−1R˙uB=[ωB]×uB
于是我们便得到:
v B = R − 1 R ˙u B = [ ω B ] ×u B \\mathbf{v}_{B}=\\mathbf{R}^{-1} \\dot{\\mathbf{R}} \\mathbf{u}_{B}=\\left[\\omega^{B}\\right]_{\\times} \\mathbf{u}_{B} vB=R−1R˙uB=[ωB]×uB
也即证明了:
d d tR = R [ ω ] × \\frac{\\mathrm{d}}{\\mathrm{~d} t} \\mathbf{R}=\\mathbf{R}[\\omega]_{\\times} dtdR=R[ω]×
感想
说实话这里的各种旋转的原因困扰了我蛮长时间,但由于并不会影响我之前的工作因此每次遇到也就放过了,询问周围的人大家也都一知半解,没办法系统清楚地进行阐述。这次过年在复习的时候突然看到IMU这块的知识,然后好奇为什么是右乘,纠结了两天查了一些资料,做了蛮多草稿,最后彻底的搞清楚了。其实就抓住两个关键点
- 讨论的是一个点/向量/位姿 还是 一个坐标系(位姿和坐标系在左乘的时候意义相同)?
- 如果讨论的是一个点/向量/位姿,那么到底是移动的他们绕着固定的坐标系在做旋转,还是固定的他们在不同坐标系之间在做位姿转换?
抓住这两个点,就可以判断清楚到底是左乘,还是右乘
最后,不得不说一句,真是太有趣了!


