电力系统节点导纳矩阵详解
一、节点导纳矩阵的形成
电力系统潮流计算的计算机算法中,由于数学模型为程序编制通用模型,因此,所有参数均需先折算为统一基准下的标幺值,模型求解后,再折算至有名值。以下内容如无特别说明,均采用标幺值描述。节点导纳矩阵形成的计算步骤和方法:
(1)节点导纳矩阵的阶数等于电力网络中除参考点(一般为大地)以外的节点数。
(2)节点导纳矩阵是稀疏矩阵,其各行非对角非零元素的个数等于对应节点所联的不接地支路数。
(3)节点导纳矩阵的非对角元素 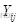 等于节点i 和j 间支路导纳的负值
等于节点i 和j 间支路导纳的负值
(4)节点导纳矩阵的对角元素,即各节点的自导纳等于相应节点所连支路的导纳之和,并包括节点对地支路。
(5)节点导纳矩阵是对称方阵,因此一般只需要求取这个矩阵的上三角或下三角部分。
(6)在节点导纳矩阵中,变压器支路一般按τ型等值电路计算,其中,变压器励磁回路直接按该节点对地导纳支路计入对角元素;而变压器τ型等值电路中的阻抗支路,则采用计及非标准变比时以导纳表示的π型二端口等值电路,如下图所示。按此等值电路用前述方法很方便地计入节点导纳矩阵,即当接入非标准变比的变压器支路i 和j 时,节点导纳矩阵各元素:
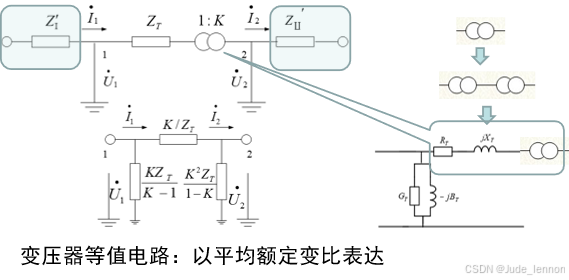
增加非零非对角元素( i 和j 之间互导纳): 
节点 i 的自导纳,除计入变压器励磁回路导纳外(励磁回路于节点 i ),增加一个改变量:
节点 j 的自导纳,增加一个改变量:
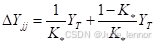
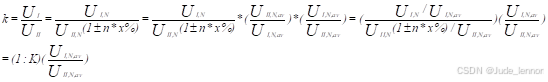
二、节点导纳矩阵的修改
对电力系统计算中,对于已知网络,其节点导纳矩阵已经形成。如果网络接线发生局部变化,此时不必重新计算节点导纳矩阵。仅仅需要在原节点导纳矩阵的基础上进行必要的局部修改就可以得到所求的节点导纳矩阵。下面介绍几种情况。
(1)从原有的网络中引出一条新的支路,同时增加一个新的节点,见图4-3(a)。设 i 为原网络N中任意节点, j 为新增加节点,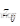 为新增加的支路阻抗。由于增加一个新的节点,因而节点导纳矩阵相应增加一阶。而且j 节点只有一条支路,所以新增加节点j 的对角元素为
为新增加的支路阻抗。由于增加一个新的节点,因而节点导纳矩阵相应增加一阶。而且j 节点只有一条支路,所以新增加节点j 的对角元素为
新增加的非对角元素为
原有网络节点 i 的自导纳增量为
将新增加对角元素、非对角元素纳入原节点导纳矩阵中即为新增加一个支路的所求节点导纳矩阵。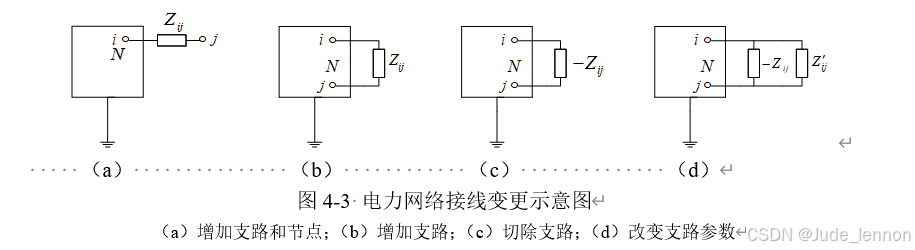
(2)在原有节点 i 和j 之间增加一条支路,见图4-3(b)。在这种情况下,增加支路,不增加节点,节点导纳矩阵的阶数不变。但是,节点 i 和j 有关的元素应作如下修正
(3)在原有网络节点 i 和j 之间切除一条阻抗为 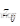 的支路,在这种情况下,相当于在节点 i 和j 之间增加一条阻抗为
的支路,在这种情况下,相当于在节点 i 和j 之间增加一条阻抗为 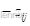 的支路,见图图4-3©。因此与节点 i 和j 有关的元素应做以下修改
的支路,见图图4-3©。因此与节点 i 和j 有关的元素应做以下修改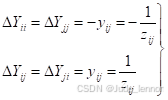
(4)原有网络节点 i 和j 之间支路阻抗由 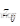 改变为
改变为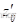 。在这种情况下,可以看作是在节点i 和j 间切除阻抗
。在这种情况下,可以看作是在节点i 和j 间切除阻抗 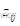 的支路,并在节点i 和j 间增加阻抗为
的支路,并在节点i 和j 间增加阻抗为 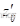 的支路,如图4-3(d)所示。此时,节点导纳矩阵的阶数不变,其元素修正如下
的支路,如图4-3(d)所示。此时,节点导纳矩阵的阶数不变,其元素修正如下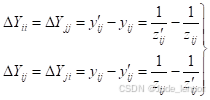
(5)原有网络节点i 和j 之间变压器的变比由 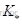 变为
变为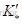 时,如下图(a)所示。相当于在网络节点i 和j 之间切除一变比为
时,如下图(a)所示。相当于在网络节点i 和j 之间切除一变比为 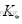 的变压器支路,而又增加一个变比为
的变压器支路,而又增加一个变比为 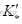 的变压器支路。变压器的等值电路见下图(b) ,其节点导纳矩阵元素的修改如下
的变压器支路。变压器的等值电路见下图(b) ,其节点导纳矩阵元素的修改如下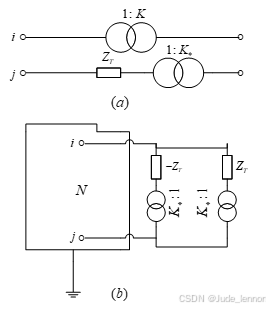
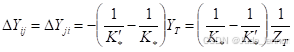
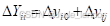
其中: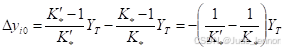
所以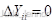
同理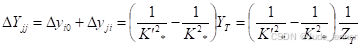
例题
【例4-1】设下图所示等值网络的阻抗、导纳均以标么值示于图中,节点编号如图中①-⑤,支路编号如图中1-5。其中,支路1和3为变压器支路。试求该网络的节点导纳矩阵。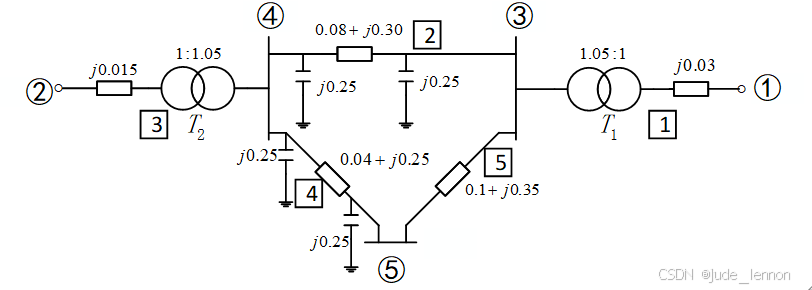
如下图4-6(a)、4-6(b)所示,为理想变压器及其等效电路图。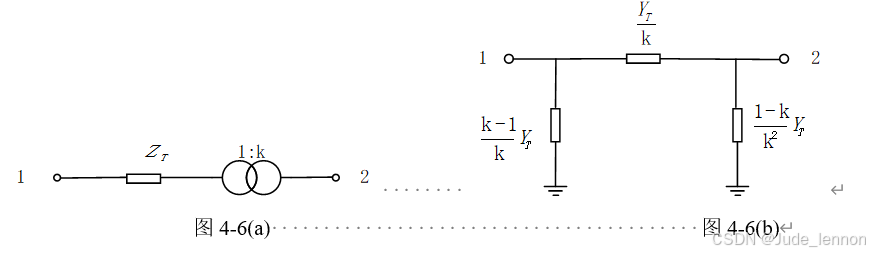
本题可用以下两种方法进行解答:
按照网络中支路输入的顺序,逐渐算入导纳矩阵各元素值。该方法等同于网络中增加支路时,导纳矩阵的修改方法。
增加支路l,起始节点i与终止节点j,则其相关的非对角元素为Yij=Yji=-yij,相关的对角元素Yii增加△Yii=yij;Yjj同理增加△Yjj=yij。首先将导纳矩阵中元素清零。
(1)在原网络中新增一条支路1, l=1,此支路起始节点为①,终止节点为③,
Y13= Y31=-y13=-yT1k1=j31.746
Y11l= Y11l-1+△Y11=yT1=-j33.333
Y33l= Y33l-1+△Y33=yT1k12=-j30.234
(2)新增一条支路2,此时有l+1,即l=2,此支路起始节点为③,终止节点为④,
Y34=Y43=-y34=-0.8299+j3.112
Y33l=Y33l-1+△Y33=Y33l-1+y34+y30
=0.8299-j33.096
Y44l=Y44l-1+△Y44=Y44l-1+y34+y40=0.8299-j2.862
(3)新增一条支路3,此支路起始节点为④,终止节点为②,此时有l=3,
Y24=Y42=-y24=-yT2k2=j63.492
Y22l=Y22l-1+△Y22=yT2+yT2k-1k=yT2=-j66.667
Y44l=Y44l-1+△Y44=Y44l-1+y24+yT21-kk2
=0.8299-j63.331
(4)新增一条支路4,此支路起始节点为④,终止节点为⑤,此时l=4,
Y45=Y54=-y45=-0.624+j3.9
Y44l=Y44l-1+△Y44=Y44l-1+y40+y45
=1.4539-j66.981
Y55l=Y55l-1+△Y55=y50+y45
=0.624-j3.65
(5)新增一条支路5,此支路起始节点为③,终止节点为⑤,此时有l=5,
Y35=Y53=-y35=-0.7547+j2.6415
Y33l=Y33l-1+△Y33=Y33l-1+y35
=1.5846-j35.7375
Y55l=Y55l-1+△Y55=Y55l-1+y35=1.3787-j6.2917
至此,所有支路均已计入导纳矩阵。
矩阵Y称为节点导纳矩阵。对角线元素Yii称为节点i的自导纳,其值等于接于节点i的所有支路的导纳之和。非对角元素Yij称为节点i、j之间的互导纳,其值等于直接连接节点i与j间的支路导纳的负值。若节点i、j之间无支路,则有Yij=0。
Yii=yi0+jyij
Yij=-yij
故,先计算出各支路导纳
y13=y31=yT1k1=- j31.746
y34=y43=10.08+j0.3=0.8299-j3.112
y24=y42=yT2k2=1j0.0151.05=-j63.492
y45=y54=10.04+j0.25=0.624-j3.9
y35=y53=10.1+j0.35=0.7547-j2.6415
y30=j0.25
y40=j0.5
y50=j0.25
由支路导纳值计算导纳矩阵各元素:
Y11= yT1= 1j0.03=-j33.333
Y22=yT2=-j66.667
Y33=y30+y13+y34+y35
=1.5846-j35.7375
Y44=y40+y34+y24+y45
=1.4539-j66.981
Y55=y50+y35+y45=1.3787-j6.2917
Y13= Y31=-y13=j31.746
Y34=Y43=-y34=-0.8299+j3.112
Y24=Y42=-y24=j63.492
Y45=Y54=-y45=-0.624+j3.9
Y35=Y53=-y35=-0.7547+j2.6415
Y12=Y21=Y14=Y41=Y15=Y51
=Y23=Y32=Y25=Y52=0
具体word可领取资源或私信我



