【图论基础】理解图的“闭环”：Tarjan 强连通分量算法全解析

• 🎓作者简介：CS专业的大一在校生
• 👨‍💻 博主主页：@Ahu_iii
• 📚 所属专栏：《基础算法》

文章目录

• 1. 什么是强连通分量？
• 2. 核心概念
• 2. 核心思想
• 3. 算法流程演示
• 4. 算法模板
• 5. 实战例题
• • 解题思路
  • 完整代码
• 6. 总结与思考

---

1. 什么是强连通分量？

强连通分量（Strongly Connected Component，SCC）：在一个有向图中，如果任意两个顶点u和v，都可以互相到达（即u能到达v，且v也能到达u），那么我们称u和v是强连通的。

一个强连通分量就是一组极大集合（不能再扩展）里的点，满足集合中的任意两点都是强连通的。

2. 核心概念

Tarjan算法是基于DFS是实现，其中核心原理在于记录访问结点的时间戳并根据时间戳来调整所属SCC的编号,即low值。

其中最主要的”主角“有：

• 时间戳 dfn[u]：记录节点u第一次被访问的时间，就像给每个节点编号；
• low值low[u]：这是算法的灵魂！表示从节点u出发，能够回溯到的最早时间戳，也可看作当前所属SCC编号；
• 栈st：存储当前 DFS 路径上的节点；
• 入栈标记in_st[u]：标记节点是否在栈中；

2. 核心思想

想象你面前有着许多房间，部分房间之间是互通的：

• 你给每个房间（节点）按访问顺序编号（dfn）
• 每次你记录从当前房间能回到的最早房间编号（low）
• 你用绳子（栈）连接你走过的路径
• 当你发现从某个房间出发的所有路径都走完了，而且这个房间的low值等于它自己的编号时，说明找到了一个\"出不去的区域\"——这就是一个强连通分量。

3. 算法流程演示

步骤 当前节点 dfn[x] / low[x] 栈状态 是否形成 SCC 弹出节点 1 1 1 / 1 [1] 否 - 2 2 2 / 2 [1, 2] 否 - 3 3 3 / 3 [1, 2, 3] 否 - 4 6，无出边 4 / 4 [1, 2, 3, 6] 是 [6] 5 回到 3 3 / min(3,4)=3 [1, 2, 3] 是 [3] 6 5 5 / 5 [1, 2, 5] 否 - 7 4 6 / 6 [1, 2, 5, 4] 否 - 8 4 → 1，1在栈内 low[4]=min(6,1)=1 [1, 2, 5, 4] 否 - 9 回到 5 low[5]=min(5,1)=1 [1, 2, 5, 4] 否 - 10 回到 2 low[2]=min(2,1)=1 [1, 2, 5, 4] 否 - 11 回到 1 low[1]=min(1,1)=1 [1, 2, 5, 4] 是 [4, 5, 2, 1]

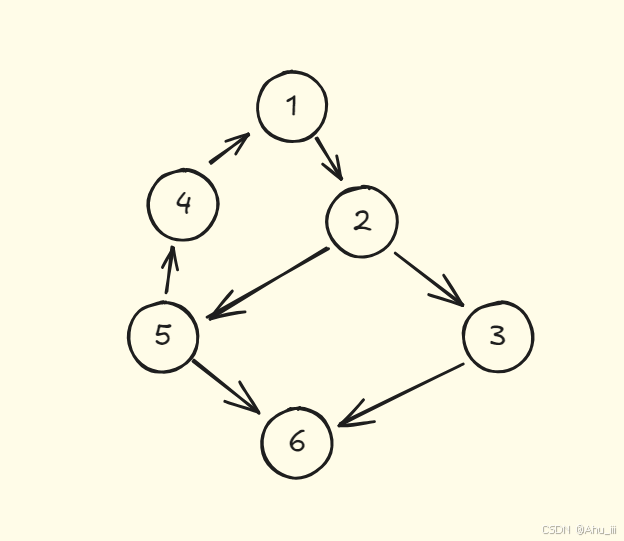
最终结果：

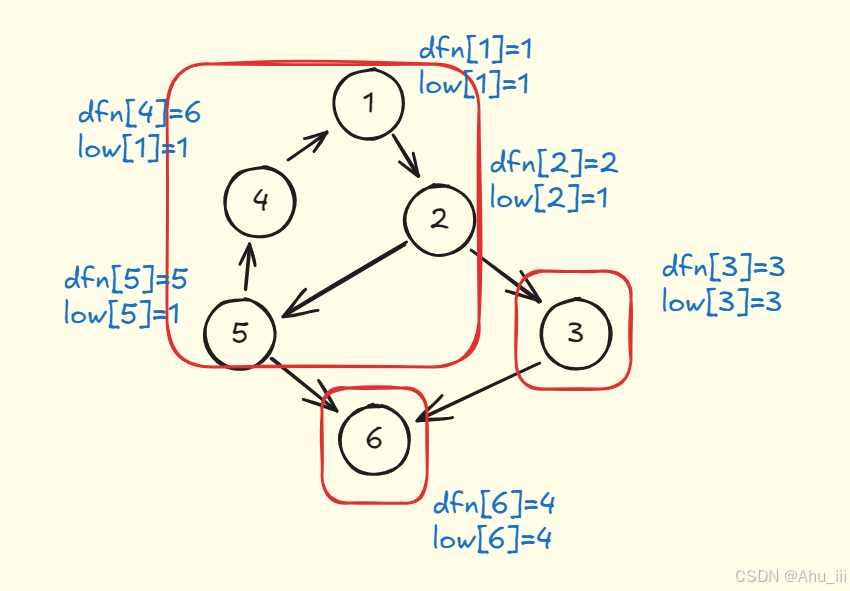
这个过程就像解开一团毛线球，每当我们发现一个\"结\"（dfn == low）时，就能扯出一团完整的毛线（强连通分量）。

4. 算法模板

#include#include #include using namespace std;const int MAXN = 1e5 + 10;vector<int> g[MAXN];int dfn[MAXN], low[MAXN], comp[MAXN];bool in_st[MAXN];int timer = 0, scc_cnt = 0;stack<int> st;void dfs(int u){dfn[u] = low[u] = ++timer;st.push(u);in_st[u] = true;for (int v : g[u]){if (!dfn[v]){dfs(v);low[u] = min(low[u], low[v]);}else if (in_st[v]) low[u] = min(low[u], dfn[v]);}if (dfn[u] == low[u]){++scc_cnt;while (1){int x = st.top(); st.pop();in_st[x] = false;comp[x] = scc_cnt; //记录scc编号if (x == u) break;}}}int main(){int n, m;cin >> n >> m;for (int i = 0; i < m; i++){int u, v;cin >> u >> v;g[u].push_back(v);}for (int i = 1; i <= n; i++) //避免遗漏不可达点if (!dfn[i]) dfs(i);for (int i = 1; i <= n; i++)cout << comp[i] << (i == n ? \'\\n\' : \' \');return 0;}

时间复杂度：$(n+m)$
空间复杂度：$O(n)$

常见应用场景：

• 缩点：将强连通分量缩成一个点，原来的有向图变成 DAG，便于进行拓扑排序等操作。
• 判断是否存在环：如果强连通分量的大小大于 1，说明存在环。

5. 实战例题

洛谷 P3387 【模板】缩点

题目描述

给定一个 $n$ 个点 $m$ 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

输入格式

第一行两个正整数 $n,m$。

第二行 $n$ 个整数，其中第 $i$ 个数 a i a_i ai​ 表示点 $i$ 的点权。

第三至 $m+2$ 行，每行两个整数 $u,v$，表示一条 $u\to v$ 的有向边。

输出格式

共一行，最大的点权之和。

输入输出样例 #1

输入 #1

2 21 11 22 1

输出 #1

2

说明/提示

对于 $100\%$ 的数据， 1≤n≤1 0 4 1\\le n \\le 10^4 1≤n≤104， 1≤m≤1 0 5 1\\le m \\le 10^5 1≤m≤105， 0≤ a i ≤1 0 3 0\\le a_i\\le 10^3 0≤ai​≤103。

• 2024-11-1 添加了 hack 数据；

解题思路

题目要求在图上DP求出一条权值和最大的路径，并说明可重复经过一条边或一个点，意味着同一SCC可直接所有点权值之和，即只需将同一scc的权值和看作一个点的权值再DP即可。

void solve() { // 1. 建图 // 2. Tarjan 找强连通分量 // 3. 缩点重新建图 // 4. 在新图上 DP 求最大权值路径}

完整代码

#include #include #include #include using namespace std;const int MAXN = 1e5 + 10;vector<int> g[MAXN], dag[MAXN];int w[MAXN], indeg[MAXN];int dfn[MAXN], low[MAXN], scc_id[MAXN],scc_val[MAXN], tim = 0, scc_cnt = 0;bool in_st[MAXN];stack<int> st;int dp[MAXN];//dp[i]表示以 i 为终点的最大和void tarjan(int u){dfn[u] = low[u] = ++tim;st.push(u);in_st[u] = true;for (int v : g[u]){if (!dfn[v]){tarjan(v);low[u] = min(low[u], low[v]);}else if (in_st[v]) low[u] = min(low[u], dfn[v]);}if (dfn[u] == low[u]){++scc_cnt;while (1){int x = st.top(); st.pop();in_st[x] = false;scc_id[x] = scc_cnt;scc_val[scc_cnt] += w[x];//将同一scc中的权值累加if (x == u) break;}}}int main(){ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++)cin >> w[i];for (int i = 0; i < m; i++){int u, v;cin >> u >> v;g[u].push_back(v);}for (int i = 1; i <= n; i++)if (!dfn[i])tarjan(i);for(int u = 1; u <= n; u++)//建新图，scc编号看作结点for(int v : g[u])if (scc_id[u] != scc_id[v]){dag[scc_id[u]].push_back(scc_id[v]);indeg[scc_id[v]]++;}queue<int> q;// topo + dp按照路径顺序转移for (int i = 1; i <= scc_cnt; i++)if (!indeg[i]){dp[i] = scc_val[i];q.push(i);}while (!q.empty()){int u = q.front(); q.pop();for (int v : dag[u]){dp[v] = max(dp[v], dp[u] + scc_val[v]);if (!(--indeg[v]))q.push(v);}}int ans = 0;for (int i = 1; i <= scc_cnt; i++)//最后需要遍历一遍找出最大值ans = max(ans, dp[i]);cout << ans;}

注：在缩点问题中，通常需要记录每个原结点属于哪个强连通分量，建议用scc_id[u]数组来记录结点u属于第几个强连通分量。

6. 总结与思考

Tarjan 强连通分量算法虽然看起来复杂，但其核心思想非常优雅：通过一次 DFS 遍历，利用时间戳和回溯信息，精准地识别出图中的所有\"小团体\"。
算法的精髓在于：

• dfn数组记录访问顺序;
• low数组记录能回溯到的最早节点;
• 栈维护当前搜索路径;
• dfn[u] == low[u]判定强连通分量的根;