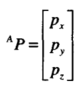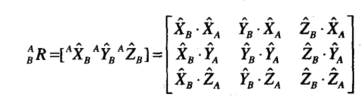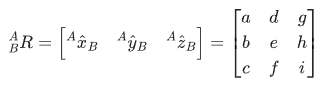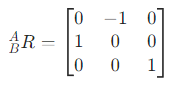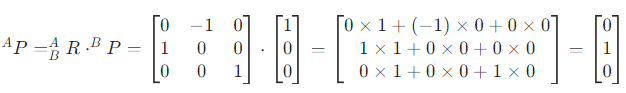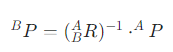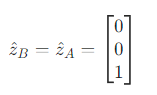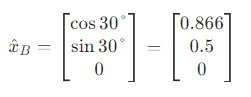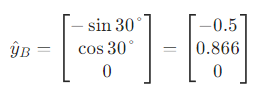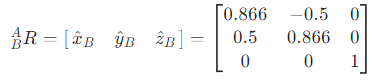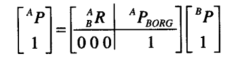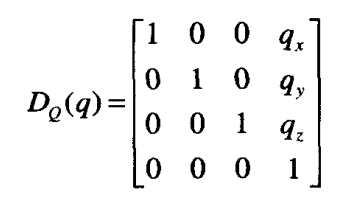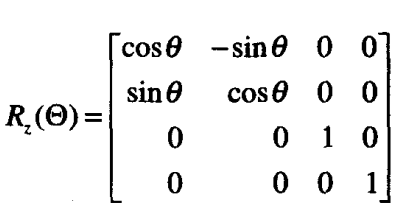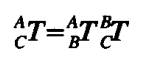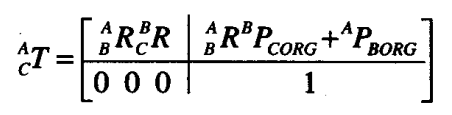机器人 - 机器人学导论（2）空间描述和变换

技术文档

一、空间描述和变换

1.1 描述

1.位置描述

2.姿态描述

3.坐标系的描述

1.2 映射

1.平移坐标系的映射

2.旋转坐标系的映射

3.关于一般坐标系的映射

1.3 算子

1.平移算子

2.旋转算子

1.4 变换算法

1.混合变换

一、空间描述和变换

1.1 描述

1.位置描述

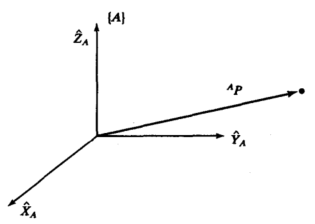
描述位置需要坐标系，可以用3x1的位置矢量对空间中的点进行描述，但是需要标注是在哪个坐标系，一般用左上标来标志，如，表示P点在A坐标系中

在坐标系A中，用矢量来表示P，如

2.姿态描述

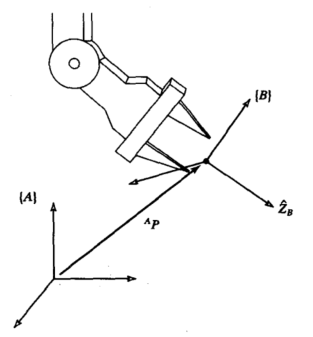
利用坐标系B原点位置相对于坐标系A的位置，来描述执行器“到了哪”，
利用B坐标系中的三轴，来确定执行器“转了多少”，

这里首先用来表示B坐标系三轴的单位矢量，接着用A坐标系表达，则可以写为

这时候可以列出一个3x3的矩阵，

首先，称这个矩阵为旋转矩阵，表示B相对于A的状态；

这部分，先不看那个A，可以认为是执行器，相对于A的状态；
展开之后，就是投影到A坐标系上面去；

PS:

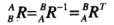
对了，单位矢量的点积可以反映出余弦角，
因为 $\\vec{a} \\cdot \\vec{b} = |\\vec{a}||\\vec{b}|cos\\theta$ ，然后单位矢量模又为1，直接得出 $cos\\theta$

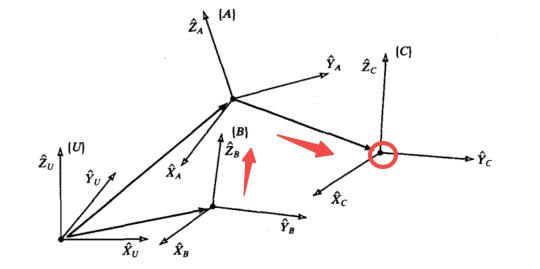
3.坐标系的描述

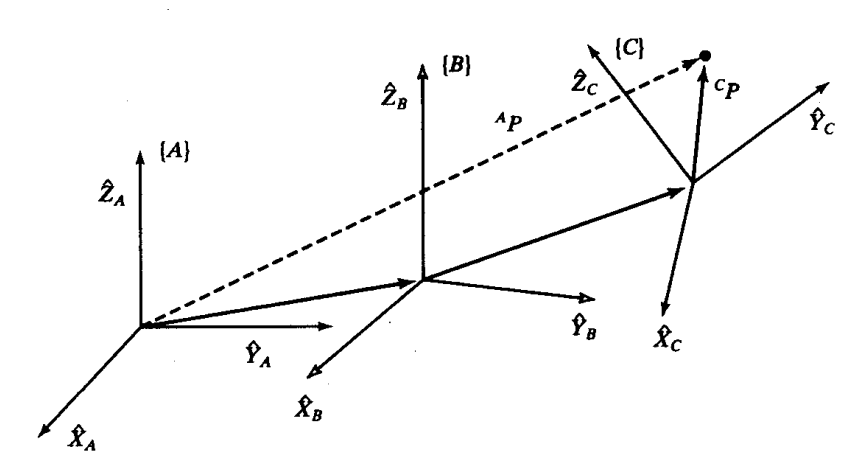
这里我个人的认为是ABC三个坐标系，分别可以表示为关节1(B)，关节2(A)，执行器(C)，
并且可以根据这些坐标系各自的单位矢量，来了解它们之间的夹角余弦值(利用点积)

1.2 映射

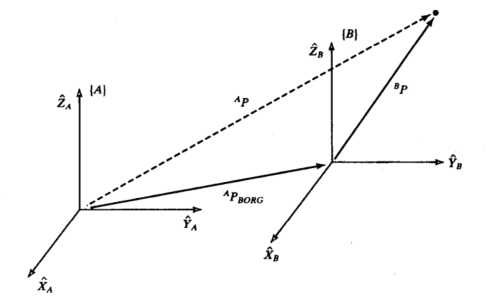
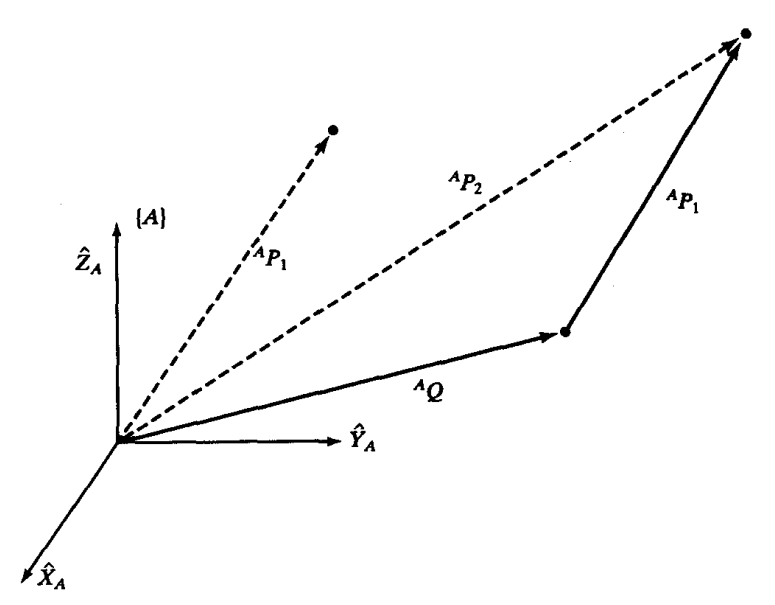
1.平移坐标系的映射

最开始我们是在【B】坐标系中用 $^{B}_{}P$ 来描述点的位置，
用 $^{B}_{}P_{BORG}$ 来描述【B】原点对于【A】的位置，
假设此时【A】【B】的姿态相同时（就像是平移过去），
这时候可以用 $^{A}_{}P=^{B}_{}P+^{A}_{}P_{BORG}$ 来描述点的位置（向量加法）

2.旋转坐标系的映射

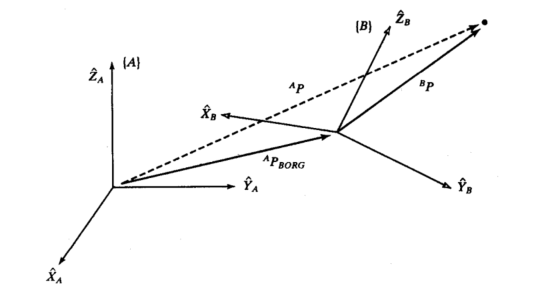
假如我们现在站在【A】坐标轴上，但是此时【A】【B】姿态不同（我们人是正的，机器人歪歪扭扭躺那里），此时我们需要用【B】的三个单位轴向量，在【A】上的坐标，来表示这个机器人有多“歪”；

假如说，现在我们站着，我们脚底下坐标轴为【A】，对面有台电动车也“站”着，它“脚底下”的坐标轴为【B】，此时一阵大风给它刮倒了，【B】“歪了”；

我们先定义一下【A】【B】坐标系中的单位矢量 $x_A,y_A,z_A,x_B,y_B,z_B$

假设，这里 $x_B$ 在坐标系【A】中表示为 $^{A}_{}x_B=(a,b,c)^T$

同理，y和z表示在【A】中表示为 $^{A}_{}y_B=(d,e,f)^T$ ， $^{A}_{}z_B=(g,h,i)^T$

那么，我们似乎可以得到一个对应关系，是个3x3的矩阵，也就是旋转矩阵；

假如这里的旋转矩阵为：

然后【B】上有一点，假设是电动车的油门吧，为 $^{B}P=(1,0,0)^T$ (在【B】点坐标系中)，也就是，电动车说，它的油门在它坐标系中的 $(1,0,0)^T$ 位置，
此时，我们要描述电动车油门对于我们的位置(在【A】坐标系中的位置)，就可以

反过来，电动车想描述我们的右手在它【B】的位置，则可以用

旋转矩阵：
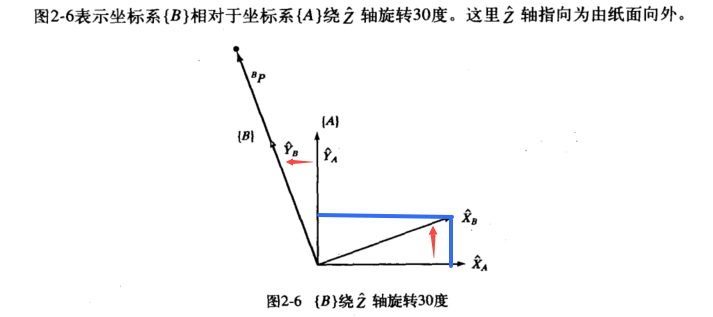
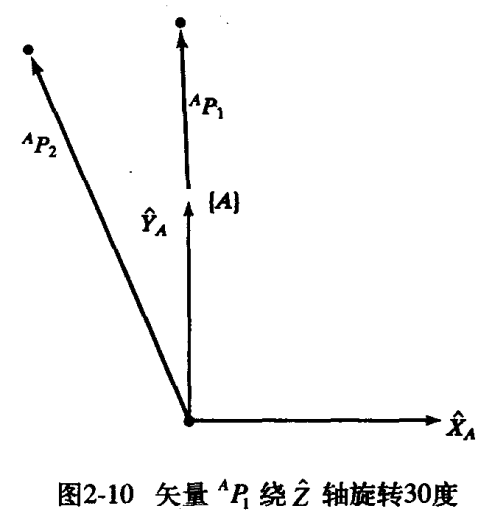
可以看上面的1.1-2 姿态描述那部分

红色箭头表示转向，便于看...
因为绕z轴旋转，所以认为z轴不变，也就是

因为旋转了30°，此时，【B】坐标系中的x相对于【A】坐标系变成了

同理，【B】坐标系中的y相对于【A】坐标系变成了

然后就可以拿到旋转矩阵了...

3.关于一般坐标系的映射

某个雨天，你站在路口，此时一个摩托佬骑着他的《得吃250SR》漂移过弯，但是因为雨天地滑，不慎侧滑摔出去了。此时怎么描述你和摩托佬...（或者他的《得吃250SR》）

我们可以先旋转，再平移（因为摩托佬摔车了，坐标系歪了。摩托佬还漂移飞出去了，他和我们也不是原点重合）；

齐次变换矩阵：
利用这个让上面的“先旋转，再平移”看着简洁一些，也方便计算机处理；
这里 ${}_B^A T$ 是一个 4x4 的矩阵；