逃生优化算法EOA可用于(动态障碍物环境下多无人机协同路径规划/云计算任务调度优化研究)
逃生优化算法(Escape Optimization Algorithm,EOA)是一种受到生物逃生行为启发而提出的智能优化算法,下面从原理、步骤、特点、应用等方面进行详细介绍:逃生优化算法EOA可用于(动态障碍物环境下多无人机协同路径规划/云计算任务调度优化研究)
算法原理
逃生优化算法模拟了生物在面临危险时的逃生行为。在自然界中,生物会感知周围环境的危险程度,根据危险信号调整自己的逃生策略,以寻找安全区域。在算法中,每个个体(解)就相当于一个生物,搜索空间则是生物所处的环境,算法通过模拟生物的逃生机制来引导个体在搜索空间中移动,从而找到最优解。
算法步骤
初始化
- 确定搜索空间的范围,即变量的上下界。
- 随机生成一定数量的个体(解),每个个体代表搜索空间中的一个点,这些个体构成初始种群。
评估适应度
- 定义适应度函数,用于衡量每个个体的优劣。适应度值越高,表示该个体越优。
- 计算初始种群中每个个体的适应度值。
确定危险区域
- 根据当前种群的分布和适应度值,确定搜索空间中的危险区域。危险区域通常是适应度值较低的区域,代表生物需要逃离的地方。
逃生操作
- 每个个体根据自身位置和危险区域的信息,调整自己的移动方向和速度,朝着更安全(适应度值更高)的区域移动。具体的移动规则可以根据不同的逃生策略进行设计,例如:
- 个体可以朝着距离最近的安全区域移动。
- 个体可以根据周围其他个体的信息,跟随适应度值较高的个体移动。
更新种群
- 根据个体的移动结果,更新种群中每个个体的位置。
- 重新计算更新后种群中每个个体的适应度值。
终止条件判断
- 判断是否满足终止条件,常见的终止条件包括达到最大迭代次数、适应度值达到预设的阈值等。如果满足终止条件,则算法结束,输出最优解;否则,返回步骤 3 继续迭代。
算法特点
优点
- 较强的全局搜索能力:逃生优化算法通过模拟生物的逃生行为,能够引导个体在搜索空间中广泛探索,避免陷入局部最优解,从而具有较强的全局搜索能力。
- 适应性强:算法可以根据不同的问题和搜索空间的特点,灵活调整逃生策略和参数,具有较好的适应性。
- 易于实现:算法的原理和步骤相对简单,实现起来较为容易,不需要复杂的数学模型和计算。
缺点
- 收敛速度较慢:由于算法注重全局搜索,可能会在搜索过程中花费较多的时间在探索不同的区域,导致收敛速度较慢。
- 参数选择困难:算法的性能受到一些参数的影响,如逃生策略的参数、种群大小等,这些参数的选择需要根据具体问题进行调整,选择不当可能会影响算法的性能。
应用领域
- 工程优化问题:在机械设计、电路设计、化工过程优化等工程领域,逃生优化算法可以用于优化设计参数,提高工程系统的性能和效率。
- 函数优化:可以用于求解各种复杂的数学函数的最优值,如高维、多峰函数等。
- 机器学习和数据挖掘:在特征选择、模型参数优化等方面,逃生优化算法可以帮助找到最优的特征子集或模型参数,提高机器学习算法的准确性和泛化能力。
逃生优化算法(Escape Optimization Algorithm, EOA)在动态障碍物环境下多无人机协同路径规划和云计算任务调度优化研究中的应用具有显著潜力。以下是具体实现方法、技术细节及案例说明:
1. 动态障碍物环境下多无人机协同路径规划
问题建模
- 目标:在动态障碍物环境中,为多无人机规划安全、高效且协同的飞行路径,需满足:
- 避障:实时避开移动障碍物(如其他无人机、飞鸟)。
- 协同:无人机间保持通信距离,避免碰撞。
- 效率:路径总长度和能耗最小化。
EOA核心策略
- 逃生行为映射:
- 分散策略:检测到障碍物时,部分无人机向不同方向分散探索新路径。
- 协作机制:通过信息素或通信共享安全路径信息,引导其他无人机跟随。
- 适应度函数:F=w1⋅∑路径长度+w2⋅最小安全距离1+w3⋅通信中断惩罚
- 动态更新规则:
- 危险感知:若无人机与障碍物距离小于阈值,触发逃生行为。
- 路径重置:随机调整部分无人机的航向角和速度,模拟逃生方向选择。
实现步骤
- 环境仿真:
- 使用ROS/Gazebo或Python(PyGame)构建动态障碍物场景。
- 定义障碍物运动模型(如随机移动或固定轨迹)。
- 算法流程:
python
class EOA_UAV: def __init__(self, num_drones): self.drones = [Drone(id=i) for i in range(num_drones)] self.obstacles = DynamicObstacles() def escape_optimize(self): for drone in self.drones: if self.obstacles.near(drone.position): # 触发分散策略:随机调整航向 drone.heading += np.random.uniform(-30, 30) drone.speed *= 1.2 else: # 协作机制:向全局最优路径靠拢 drone.update_path(self.global_best_path) return self.global_best_path - 验证指标:
- 路径安全性:无人机与障碍物最小距离。
- 协同效率:任务完成时间、总航程。
- 实时性:算法单次迭代耗时(需<100ms)。
案例与改进
- 课题示例:
《基于EOA的多无人机动态协同搜救路径规划》- 场景:山区灾害救援,无人机需避开移动障碍(如落石)。
- 改进:引入分级危险响应,根据障碍物速度动态调整逃生幅度。
- 可视化:在RViz或Matplotlib中绘制3D路径与障碍物轨迹。
2. 云计算任务调度优化研究
问题建模
- 目标:在云计算环境中,将任务合理分配到虚拟机(VM),满足:
- 负载均衡:避免部分VM过载,其他VM闲置。
- 成本效率:最小化任务完成时间和资源租赁成本。
- 优先级约束:高优先级任务优先调度。
EOA核心策略
- 逃生行为映射:
- 资源竞争:过载VM触发任务迁移(类似个体逃离危险区域)。
- 安全区域:空闲VM作为“安全目标”,吸引任务分配。
- 适应度函数:F=α⋅总任务完成时间+β⋅资源成本+γ⋅负载均衡方差
- 动态规则:
- 过载检测:当VM的CPU利用率 > 80%,标记为“危险节点”。
- 任务迁移:将危险节点上的任务迁移至低负载VM。
实现步骤
- 仿真环境搭建:
- 使用CloudSim或Python模拟云计算任务(任务大小、优先级)和VM资源。
- 算法流程:
python
class EOA_Scheduler: def __init__(self, tasks, vms): self.tasks = tasks # 任务列表(大小、优先级) self.vms = vms # 虚拟机列表(CPU、内存) def optimize(self): for task in self.tasks: # 初始分配:按优先级选择VM vm = self.select_vm_by_priority(task) vm.assign(task) # 逃生检测:若VM过载,迁移任务 if vm.load > 0.8: safe_vm = self.find_safest_vm() vm.migrate(task, safe_vm) return self.calculate_fitness() - 验证指标:
- 任务完成时间:所有任务从提交到结束的平均时间。
- 资源利用率:VM的CPU/内存使用率方差。
- 成本:按VM使用时长计算的租赁费用。
案例与改进
- 课题示例:
《EOA驱动的边缘计算任务动态卸载策略》- 场景:边缘服务器资源有限,需将任务动态卸载到云端。
- 改进:设计自适应权重(α,β,γ),根据网络延迟动态调整。
- 数据来源:使用Google Cluster Data公开数据集进行测试。
EOA在两类场景中的对比总结
实施建议
- 代码开源与复现:
- 无人机路径规划:提供ROS包或Jupyter Notebook代码。
- 任务调度:发布Python脚本与测试数据集(如随机生成的任务列表)。
- 可视化分析:
- 路径规划:绘制无人机轨迹与障碍物动态变化图。
- 任务调度:生成甘特图展示任务分配时间线。
- 对比实验设计:
- 对比传统算法(如PSO、蚁群算法)在相同场景下的性能。
创新课题方向
- 动态无人机路径规划:
- 《基于EOA与强化学习的多无人机动态避障联合优化》
- 《逃生行为启发的无人机集群通信拓扑抗毁性研究》
- 云计算任务调度:
- 《EOA驱动的多云环境任务容错调度算法》
- 《边缘-云端协同任务卸载的逃生优化策略》
总结
EOA通过模拟生物逃生行为中的动态响应与协作机制,在动态路径规划和任务调度中展现出以下优势:
- 实时性:快速响应环境变化(如障碍物移动、VM过载)。
- 全局优化:通过分散策略避免局部最优,提升解的质量。
- 跨学科适用性:算法框架可灵活适配不同领域的优化问题。
具体代码及实验结果
%% 清除命令窗口、工作区变量并关闭所有图形窗口clcclearclose all%%%% 算法参数设置与目标函数信息获取% 选择测试函数的名称,可从 \'F1\' 到 \'F23\' 中选取Fun_name = \'F4\'; % 设定搜索代理的数量,即参与搜索的个体数量SearchAgents = 30; % 设定最大迭代次数,算法将在达到该迭代次数后停止Max_iterations = 1000; % 调用 fun_info 函数,获取所选测试函数的相关信息% lowerbound 为变量的下界,upperbound 为变量的上界,dimension 为问题的维度,fitness 为目标函数句柄[lowerbound, upperbound, dimension, fitness] = fun_info(Fun_name); % 调用 ESC 函数进行优化计算% Best_score 为找到的目标函数的最优值,Best_pos 为对应的最优解,ESC_curve 为收敛曲线数据[Best_score, Best_pos, ESC_curve] = ESC(SearchAgents, Max_iterations, lowerbound, upperbound, dimension, fitness); %%% 显示 ESC 算法找到的最优解display([\'The best solution obtained by ESC for \' [num2str(Fun_name)],\' is : \', num2str(Best_pos)]);% 显示 ESC 算法找到的目标函数的最优值display([\'The best optimal value of the objective funciton found by ESC for \' [num2str(Fun_name)],\' is : \', num2str(Best_score)]);% 创建一个新的图形窗口,并设置其位置和大小figure(\'Position\', [454 445 694 297]);% 在图形窗口中创建一个 1x2 的子图布局,并选择第一个子图subplot(1, 2, 1);% 调用 func_plot 函数绘制所选测试函数的图形func_plot(Fun_name); % 设置子图的标题为“Parameter space”title(\'Parameter space\')% 设置 x 轴标签为“x_1”xlabel(\'x_1\');% 设置 y 轴标签为“x_2”ylabel(\'x_2\');% 设置 z 轴标签为测试函数名及变量名zlabel([Fun_name,\'( x_1 , x_2 )\'])% 选择第二个子图subplot(1, 2, 2); % 确定绘制收敛曲线时取点的数量CNT = 20;% 从 1 到最大迭代次数均匀选取 CNT 个点并取整k = round(linspace(1, Max_iterations, CNT)); % 注意:如果收敛曲线画出来的点很少,随机点很稀疏,说明点取少了,这时应增加取点的数量,100、200、300等,逐渐增加% 相反,如果收敛曲线上的随机点非常密集,说明点取多了,此时要减少取点数量% 定义迭代次数序列iter = 1:1:Max_iterations;% 判断测试函数是否为 \'F16\'、\'F9\' 或 \'F11\'% 因为这几个函数收敛太快,不适用于 semilogy 函数,直接使用 plot 函数绘制if ~strcmp(Fun_name, \'F16\') && ~strcmp(Fun_name, \'F9\') && ~strcmp(Fun_name, \'F11\') % 使用对数坐标绘制收敛曲线 semilogy(iter(k), ESC_curve(k), \'k-o\', \'linewidth\', 1);else % 使用线性坐标绘制收敛曲线 plot(iter(k), ESC_curve(k), \'k-o\', \'linewidth\', 1);end% 设置 x 轴标签为“Iteration#”xlabel(\'Iteration#\');% 设置 y 轴标签为“Best fitness so far”ylabel(\'Best fitness so far\');% 添加图例,标识为 ESC 算法的收敛曲线legend(\'ESC\');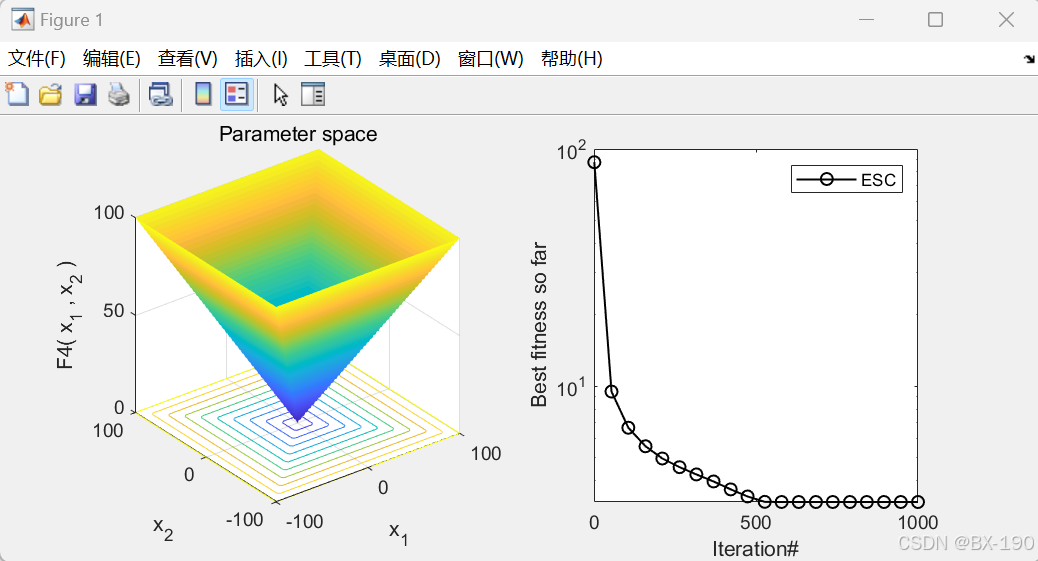
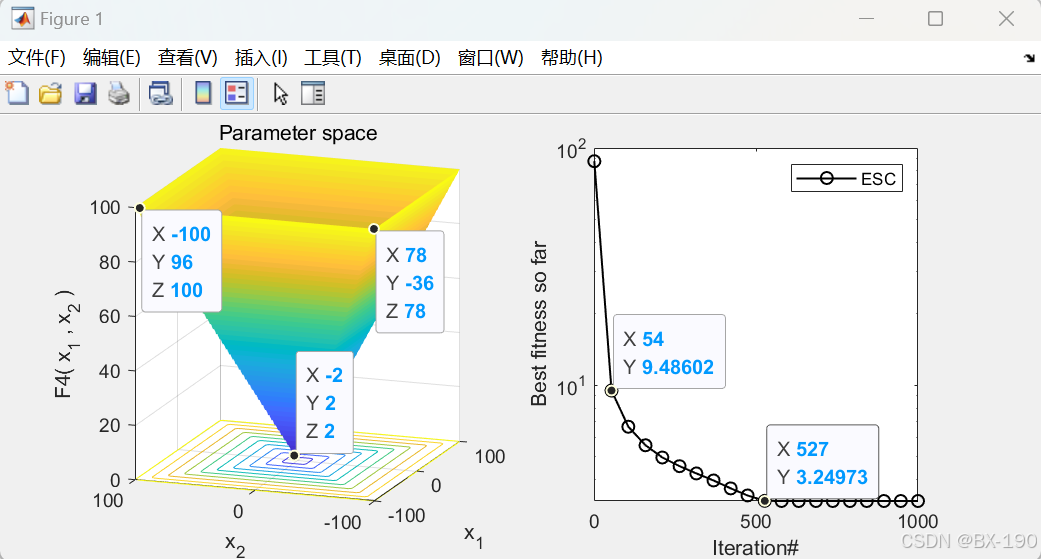
逃生优化算法实验结果简述
最优解和最优值
通过代码输出的 Best_pos 和 Best_score,可以直接得到逃生优化算法(ESC)在所选测试函数 Fun_name 上找到的最优解和对应的最优值。最优解表示在搜索空间中使得目标函数取得最优值的点,而最优值则反映了算法在该测试函数上的优化效果。例如,如果 Best_score 的值很小,说明算法在该测试函数上找到了一个较好的解。
收敛曲线分析
- 绘制方式:根据测试函数的不同,代码采用了不同的绘制方式。对于大部分函数,使用
semilogy函数以对数坐标绘制收敛曲线,这有助于更清晰地观察适应度值在较小范围内的变化;而对于F16、F9和F11这几个收敛速度较快的函数,使用plot函数以线性坐标绘制。 - 收敛速度:从收敛曲线可以观察到算法的收敛速度。如果曲线在迭代初期就快速下降,说明算法能够在较短的时间内找到较好的解,收敛速度较快;反之,如果曲线下降缓慢,则收敛速度较慢。
- 收敛精度:收敛曲线最终收敛到的适应度值反映了算法的收敛精度。收敛到的适应度值越小,说明算法的收敛精度越高,能够更接近目标函数的最优值。
综合最优解、最优值和收敛曲线的分析,可以全面评估逃生优化算法在所选测试函数上的性能表现。
具体算法及优化思路和优化方法请跳转“逃生优化算法EOA可用于(动态障碍物环境下多无人机协同路径规划/云计算任务调度优化研究)”


