基于CORDIC算法在FPGA上实现开方_fpga cordic
前言
CORDIC(Coordinate Rotation Digital Computer)是坐标旋转数字计算机算法的简称,由Vloder于1959年首次提出。算法最初设计用于高效计算三角函数、反三角函数和开方等运算的实时计算问题。其核心是提供一种数学计算的逼近方法。由于它最终可分解为一系列的加减和移位操作,故非常适合硬件实现。
1.公式推导
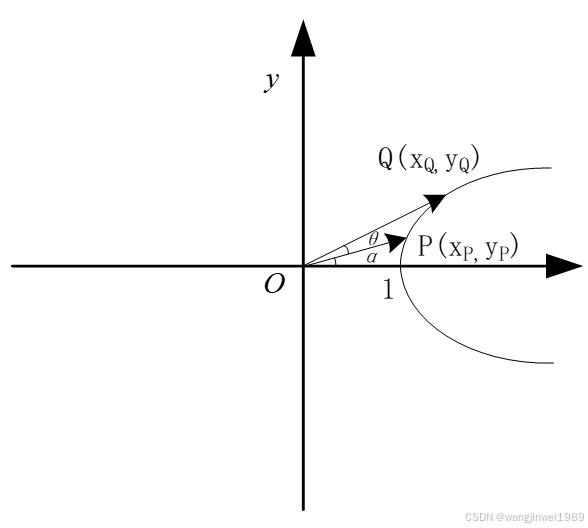
图1
如图1所示,在等轴双曲线的右半支上,向量OP与X正半轴夹角为α,故P点坐标可表示为
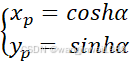 (1)
(1)
将向量OP逆时针旋转θ角至向量OQ,此时OQ与X轴正半轴夹角为α+θ,故Q点坐标可表示为
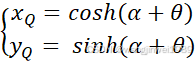 (2)
(2)
这里定义θ为目标旋转角度。根据双曲函数公式可将式(2)展开为
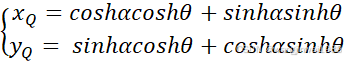 (3)
(3)
将(1)代入式(3)可得
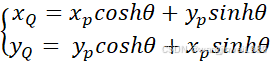 (4)
(4)
提取公因式coshθ,式(4)可重写为
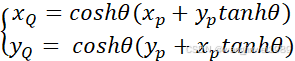 (5)
(5)
将coshθ看作固定值,若先去掉coshθ,则上式变为
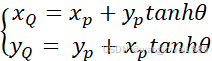 (6)
(6)
对于旋转,可将θ分解为一系列的微小角度的和,即
![]() (7)
(7)
这样,一次旋转可分解成一系列的微旋转。由(6)可知,第i+1次旋转后的结果为
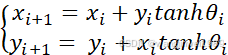 (8)
(8)
令
![]() (9)
(9)
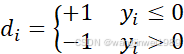 (10)
(10)
所以有
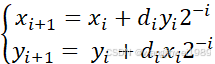 (11)
(11)
经过n(n→∞)次旋转,得到的最终结果为
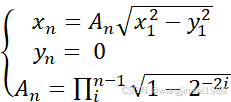 (12)
(12)
2.平方根问题的建模
已知一个大于0的数S,计算,若构造方程
,当y→0时,x→
。这便是上面公式(12)的形式。
在双曲旋转模式下,CORDIC通过调整迭代参数实现平方根计算,由迭代公司(11)逐次迭代,求取。
3.平方根算法的完整迭代过程
a.选择x1=S+0.25, y1=S−0.25,满足,
b.由公式(11)得,x2= x1−y1*,y2=y1−x1*
(d1=-1,由公式(10)所得)。依次类推。
c.值得注意的是,双曲系统的迭代较为复杂,其迭代过程要求当迭代顺序呈为4、13、40等满足i=3k+1时,该次迭代必须重复,才能保证收敛,而迭代过程变不i=1,2,3,4,4,5……。An≈0.8281593609602157。所以最终![]()
4.边界条件
S∈[0.5,2),当输入S超出[0.5, 2]时,分解S=⋅M,其中0.5≤M<2,计算
后恢复结果:
![]()
5.MATLAB实现
function sqrt_val = cordic_sqrt(S, num_iter)% CORDIC平方根算法实现% 输入:% S - 要计算平方根的正实数% num_iter - 迭代次数(建议>=16)% 输出:% sqrt_val - 计算结果%% 步骤1:输入归一化处理(将S映射到[0.5, 2)区间)[normalized_S, exp_shift] = normalize_input(S);%% 步骤2:CORDIC初始化x = normalized_S + 0.25;y = normalized_S - 0.25;K = 0.8281593609602157; % 预计算的双曲缩放因子%% 步骤3:双曲CORDIC迭代for n = 1:num_iter % 双曲模式需要重复某些迭代(n=4,13,40...) if ismember(n, [4,13,40]) % 常见重复点 repeat_flag = true; else repeat_flag = false; end % 迭代核心 for r = 1:(1 + repeat_flag) % 重复执行两次 sigma = -sign(y); % 方向判断 if sigma == 0 sigma = 1; % y=0时保持方向 end delta = y * 2^(-n); x_new = x + sigma * delta; delta = x * 2^(-n); y_new = y + sigma * delta; x = x_new; y = y_new; endend%% 步骤4:结果补偿和恢复sqrt_normalized = x / K; % 补偿缩放因子sqrt_val = sqrt_normalized * 2^exp_shift; % 恢复归一化%% 辅助函数:输入归一化function [S_norm, exp_out] = normalize_input(S_in) if S_in <= 0 error(\'输入必须为正实数\'); end % 分解为 S = 2^(2k) * M, 其中0.5 <= M = 2 M = M / 4; exp_out = exp_out + 1; end % 处理过小值 while M < 0.5 M = M * 4; exp_out = exp_out - 1; end S_norm = M;endend6.FPGA实现
将以上MATLAB实现转化为Verilog代码,程序采用三段式状态机实现。该代码采用Q16.16定点数格式,迭代次数可参数设置(含重复迭代)。S输入范围≥0,程序会对超出[0.5, 2)的数自行缩放处理。由于S范围大,造成其结果精度精确于小数点后百分位到千分位。
module CORDIC_Sqrt #( parameter INPUT_WIDTH = 32, parameter ITERATIONS = 8)( input wire clk , input wire rst , input wire start , input wire [INPUT_WIDTH-1:0] S , output wire [INPUT_WIDTH-1:0] sqrt , output reg done ); localparam IDLE = \'d0 , NORM = \'d1 , XY_INT = \'d2 , CORDIC = \'d3 , SCALE = \'d4 , FINISH = \'d5 ; reg [FINISH:0] ST, NxST ; reg [31:0] S_norm = 32\'d0 ; reg [7:0] exp_shift ; reg left ; reg signed [31:0] x, y = 0 ; reg [5:0] iter ; wire repeat_flag ; reg repeat_sign ; wire signed [31:0] sigma ; reg [47:0] sqrtleft16 ; localparam K = 32\'h0001351e; //缩放因子 1/0.8281593609602157<<16always @(posedge clk or posedge rst) begin if (rst) ST <= \'d1; else ST = 32\'h00008000 & S_norm = ITERATIONS) NxST[SCALE] = 1\'b1; else NxST[CORDIC] = 1\'b1; ST[SCALE] : NxST[FINISH] = 1\'b1; ST[FINISH] : NxST[IDLE] = 1\'b1; default : NxST[IDLE] = 1\'b1; endcaseendalways @(posedge clk) begin if (start) begin S_norm <= S; exp_shift = 32\'h00020000) begin S_norm > 2; exp_shift <= exp_shift + 1; end else if (S_norm < 32\'h00008000) begin S_norm <= S_norm << 2; exp_shift <= exp_shift + 1; end else begin S_norm <= S_norm; exp_shift <= exp_shift; end endalways @(posedge clk or posedge rst) begin if (rst) left = 2) left <= 1\'b1; else left <= 1\'b0; end else left <= left;endalways @(posedge clk) begin if (ST[XY_INT]) begin x <= S_norm + 32\'h00004000; y <= S_norm - 32\'h00004000; iter <= 6\'d1; end else if (ST[CORDIC]) begin // 更新x,y x >> iter); y >> iter); iter <= repeat_flag ? iter : iter + 1; endend always @(posedge clk or posedge rst) begin if (rst) sqrtleft16 <= \'d0; else if (ST[SCALE]) sqrtleft16 >> 16; else if (ST[FINISH]) begin if (left) sqrtleft16 <= sqrtleft16 << exp_shift; else sqrtleft16 > exp_shift; end end always @(posedge clk or posedge rst) begin if (rst) done <= 1\'b0; else if (ST[FINISH]) done <= 1\'b1; else done <= 1\'b0;end always @(posedge clk or posedge rst) begin if (rst) repeat_sign <= 1\'b0; else if (repeat_flag) repeat_sign <= 1\'b1; else repeat_sign 0) ? -1 : 1;assign sqrt = sqrtleft16[31:0];endmodule7.测试验证代码 (Testbench)
module cordic_sqrt_tb();reg clk, reset, start;reg [31:0] S;wire [31:0] sqrt;wire done;// 实例化CORDIC模块CORDIC_Sqrt uut ( .clk(clk), .rst(reset), .start(start), .S(S), .sqrt(sqrt), .done(done));initial begin clk = 0; forever #5 clk = ~clk;end// 测试用例initial begin reset = 1; start = 0; #20 reset = 0; // 测试1: 计算sqrt(20) = 4.47213595 S = 32\'d20 << 16; // Q16.6?20.0?? #15 start = 1; #10 start = 0; wait(done); $display(\"sqrt(20) = %f (Q16.16: 0x%h)\", $itor(sqrt)/65536.0, sqrt); // 测试2: 计算sqrt(0.1) = 0.316227766 #20; S = 32\'d6554; // 0.1 in Q16.16 (0.1*65536=6553.6 ? 6554) #10 start = 1; #10 start = 0; wait(done); $display(\"sqrt(0.1) = %f (Q16.16: 0x%h)\", $itor(sqrt)/65536.0, sqrt); #10 ; $stop;endendmodule8.仿真结果

参考文献
基于FPGA的数字信号处理(第2版)高亚军 编著


