图论最短路径-Dijkstra算法
最短路径:对应不带权图则表示起始点到目标点的所用的最少边数的路径;对应带权图则表示起始点到目标点的权值之和最小的路径。
Dijkstra核心思想:采用贪心策略,先找到离起点最近且未确定其最短路径的点,更新起点到其点的最小路径。并且记录已经确定最短路径的点。
举个例子:
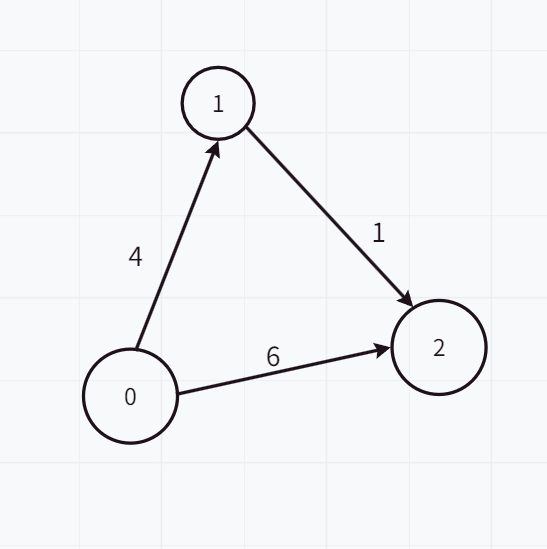
假设0到1的路径为最短路径,对于点2,目前0-2的路径为6,但是如果通过点1再到点2,则路径为5,所以更新0到2的最短路径为5,按照这个的思想一直执行下去。
给出一个有向带权图:
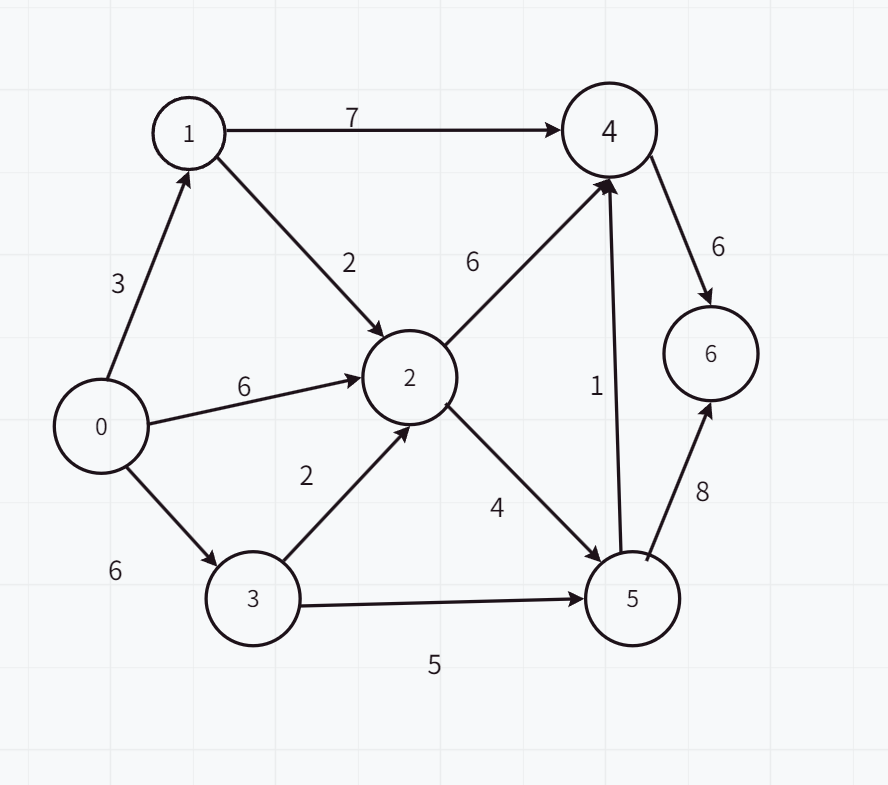
假设0为起始点
定义一个最短距离dis[7],表示0到剩余点的目前最短距离(未求状态下)
定义一个S[7]数组,用于记录已求出最短距离的点,对应索引的数组值为1表示已求出最短距离,0为未求出。
定义一个path[7]用于存放路径,各个索引对应的值为其索引的上一个点,-1则代表没有路径
初始化:
for (int i = 0;i < 7;i++) { dis[i] = g[v][i]; //初始化dis,表示v到各个点的距离 S[i] = 0; //初始化S,表示还没有求出v到其索引的最短路径if (g[v][i] < INF) { //如果v到剩余点有直接路径,则表示i点前一个点为v,否则为-1表示没有直接路径path[i] = v;}else {path[i] = -1;}}将dis初始化为0到各个点的直接距离,dis={0 ,4 ,6 ,6 ,INF,INF,INF}
将S初始化为0,表示还未求出最短路径 S={0,0,0,0,0,0,0}
如果直接距离存在(小于INF),将存在路径的点的上一个点赋为起始点0,否则为-1;path={0,0,0,0,-1,-1,-1}
S[v] = 1;path[v] = v; //将v加入S中,v的上一个结点就是本身将起始点S[v]赋为1,其上一个点为本身;S={1,0,0,0,0,0,0}
for (int i = 0;i < 6;i++) { //一共7个结点,求出v到剩下6个结点的最短路径min = INF; for (int j = 0;j < 7;j++) { //找到v到其他点直接路径的最小值if (S[j] == 0 && dis[j] < min) {k = j;min = dis[j];}}S[k] = 1; //将k加入S,表示k点已找到v到k点的最小路径for (int j = 0;j < 7;j++) { //在未求出最小路径的集合中,如果通过k点到j点+v到k点的最小路径值<目前v到j点的值if (S[j] == 0&& g[k][j]<INF && dis[k] + g[k][j] < dis[j]) {dis[j] = dis[k] + g[k][j]; //则更新dis[j]的值,表示v到j的最小路径值path[j] = k; //并且把k作为j点的上一个点}}}求出dis中最小且未确定最短路径的点,找到最短路径的点k,将他的S值赋为1;
遍历7个点找到未确定最短路径的点,并且存在k点到其点j的边,如果0到k点的最短路径+k到其点j<0到该点j目前的最短路径,则更新0到该点j的路径值,并且j的上一个点为k。
例如:
从dis中找到最短且未确定的点,也就是1,其值为4,则4这个值必定为0到1的最短路径(因为在不考虑权值为负数的情况下,0到其他点的值都>=4,无论是否通过间接点到1上,都是大于4的);
找到1后将则dis={0 ,4 ,6 ,6 ,INF,INF,INF},S={1,1,0,0,0,0,0},path={0,0,0,0,-1,-1,-1}
接着在剩下的点中找到,1到未确定点存在边且0到1的最小路径+1到 j 点<dis[ j ](目前0到 j 点的值)
也就是点2和点4,
对于点2,目前已知0到2的最小值为6,但是0到1的值也就是(dis[1])+1到2(g[1][2])的值<6(dis[2]),
则开始更新0到2的目前最小值为5,且2的上一个点更新为1,dis={0 ,4 ,5 ,6 ,INF,INF,INF},path={0,0,1,0,-1,-1,-1}
对于点4,目前已知0到4的INF,但是0到1的值也就是(dis[1])+1到4(g[1][4])的值<INF(dis[4]),
则开始更新0到4的目前最小值为11,且4的上一个点更新为1,dis={0 ,4 ,5 ,6 ,11,INF,INF},path={0,0,1,0,1,-1,-1}
接下来重复此步骤,直到算到点6为止
输出路径和权值:
void dispath(int v) { // 用于输出v到各点的最小路径值以及路径for (int i = 0;i = 0;j--) {printf(\"%d \", path1[j]);}printf(\"\\n\");}}}}对于非起始点的点,且已经求出最短路径,如果path=-1则无路径,否则逆序输出路径
例如0到5,输出权值为9,5的上一个结点为2,也就是path[5]=2;2的上一个点为1,即path[2]=1;
1的上一个结点为0,即path[1]=0;按照这样逆序存入数组path1,并输出,即:0,1,2,5
结果如下:

代码如下:
#includeusing namespace std;const int INF = 1e9;int g[7][7] = { //连通图邻接矩阵{0 ,4 ,6 ,6 ,INF,INF,INF},{INF,0 ,1 ,INF,7 ,INF,INF},{INF,INF,0 ,INF,6 ,4 ,INF},{INF,INF,2 ,0 ,INF,5 ,INF},{INF,INF,INF,INF,0 ,INF,6 },{INF,INF,INF,INF,1 ,0 ,8 },{INF,INF,INF,INF,INF,INF,0 }};int dis[7] = { 0 }; //存起始点到各个顶点的最短路径int path[7] = { 0 }; //存起始点到各个顶点的路径int S[7] = { 0 }; //若为0表示未求出到起始点其索引的最短路径,若为1则表示求出起始点其索引的最短路径void dispath(int v);void Dijkstra(int v) {for (int i = 0;i < 7;i++) { dis[i] = g[v][i]; //初始化dis,表示v到各个点的距离 S[i] = 0; //初始化S,表示还没有求出v到其索引的最短路径if (g[v][i] < INF) { //如果v到剩余点有直接路径,则表示i点前一个点为v,否则为-1表示没有直接路径path[i] = v;}else {path[i] = -1;}}S[v] = 1;path[v] = v; //将v加入S中,v的上一个结点就是本身int min = INF,k; for (int i = 0;i < 6;i++) { //一共7个结点,求出v到剩下6个结点的最短路径min = INF; for (int j = 0;j < 7;j++) { //找到v到其他点直接路径的最小值if (S[j] == 0 && dis[j] < min) {k = j;min = dis[j];}}S[k] = 1; //将k加入S,表示k点已找到v到k点的最小路径for (int j = 0;j < 7;j++) { //在未求出最小路径的集合中,如果通过k点到j点+v到k点的最小路径值<目前v到j点的值if (S[j] == 0&& g[k][j]<INF && dis[k] + g[k][j] < dis[j]) {dis[j] = dis[k] + g[k][j]; //则更新dis[j]的值,表示v到j的最小路径值path[j] = k; //并且把k作为j点的上一个点}}}dispath(v);//输出}void dispath(int v) { // 用于输出v到各点的最小路径值以及路径for (int i = 0;i = 0;j--) {printf(\"%d \", path1[j]);}printf(\"\\n\");}}}}int main() {int v;cin >> v; //输入起始点Dijkstra(v);return 0;}总的来讲: Dijkstra就是找到未确定且路径最短的点,且比较其邻接点的已知最短路径和通过间接点的路径,来判断是否需要更新最短路径。
此篇文章用于给自己巩固知识点,如果帮助到大家也是非常荣幸,如果文章有错误,感谢批评和指出


