动态规划学习---背包问题
2025---3.27,背包问题专练
DP问题的分析我们采用特定的方法
这个分析方法我们可以专门来学习一下
链接:https://www.bilibili.com/video/BV1X741127ZM
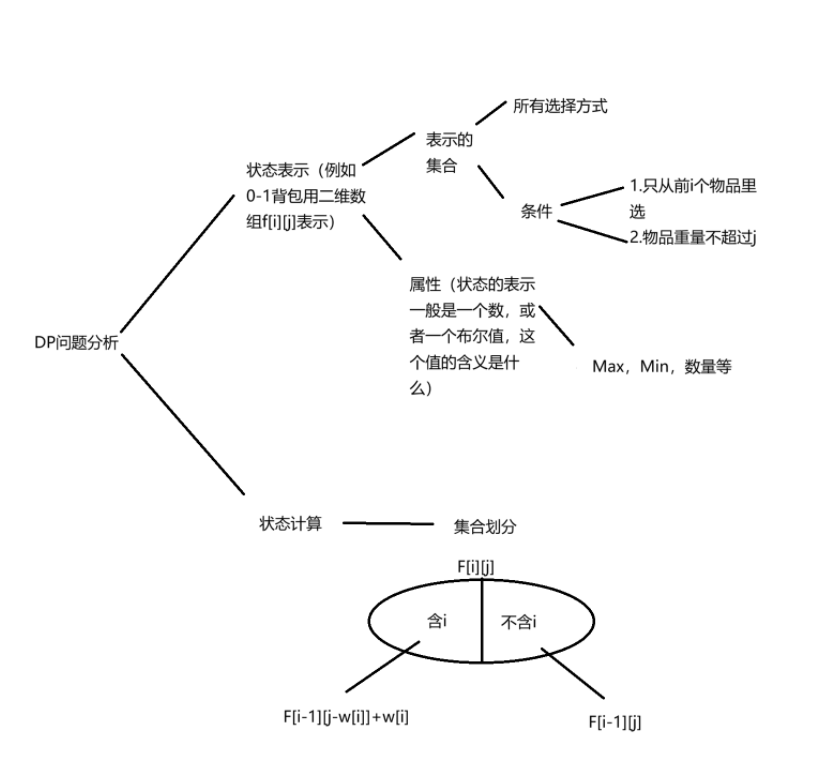
0-1背包问题
2. 01背包问题 - AcWing题库
由上面的分析我们可以轻松得到0-1背包的状态计算方程
if(j>=w[i])F[i][j]=max(F[i-1][j],F[i-1][j-w[i]]+w[i]);下面我们对于一个完整的0-1背包问题,给出完整代码,再来讨论从二维优化到一维
#include const int N=1010;using namespace std;int V[N],W[N];//体积和重量int f[N][N];//状态表示int n,v;int main(){ cin>>n>>v; for(int i=1;i>a>>b; V[i]=a; W[i]=b; } for(int i=1;i<=n;i++)for(int j=0;j=V[i])f[i][j]=max(f[i-1][j],f[i-1][j-V[i]]+W[i]);} cout<<f[n][v]; return 0;}接下来我们考虑一下如何进行优化,我们可以发现,对于 F[i][j],无论是哪种情况都只用到了F[i-1]这一层,因此我们可以从二维化成一维,因为相当于我们每一层的F[j],在对F[j]的数量进行处理之前都是F[i-1][j],所以我们根本不需要存储第一维度的值
简单来说就是,假设现在的i=2,此时我们只有F[j]一列数字,这一列数字其实是,上一轮循环得到的也就是i=1的时候得到的,就是原来二维里面的第i-1层,所以我们只需要在这个基础上进行修改就行,而改成一维怎么改呢
就变成了
F[j]=max(F[j],F[j-V[i]]+W[i])
那么我们要保证的是我们是基于上一层也就是F[i-1][j]的基础上进行修改的,所以应该倒序
假设 j从V[i]开始,到v结束
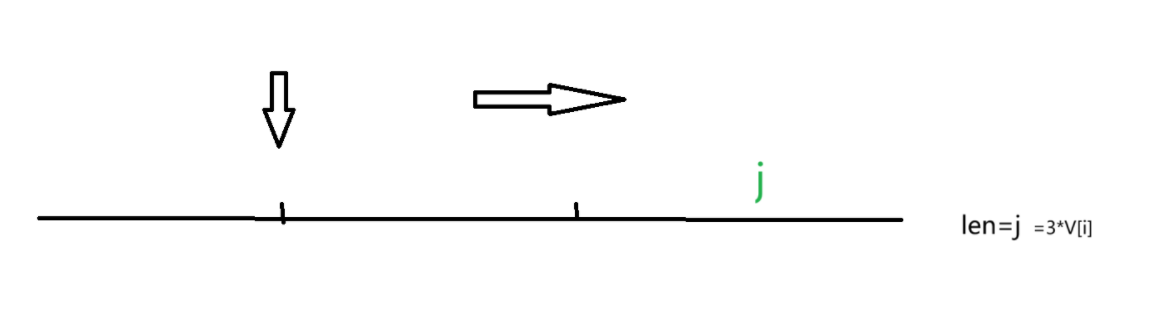
当j往后移动到时候,前面的值已经改变,就不再是第i-1层的了
所以正确的方式是j从后往前遍历对于 0到V[i]的值没有变化,所以是从v遍历到V[i]
for(int i=1;i=V[i];j--){ f[j]=max(f[j],f[j-V[i]]+W[i]);} 完全背包问题
在0-1背包的基础上,每个物品的数量不限
3. 完全背包问题 - AcWing题库
在掌握0-1背包的分析方法后,完全背包问题的分析就很简单了,如图
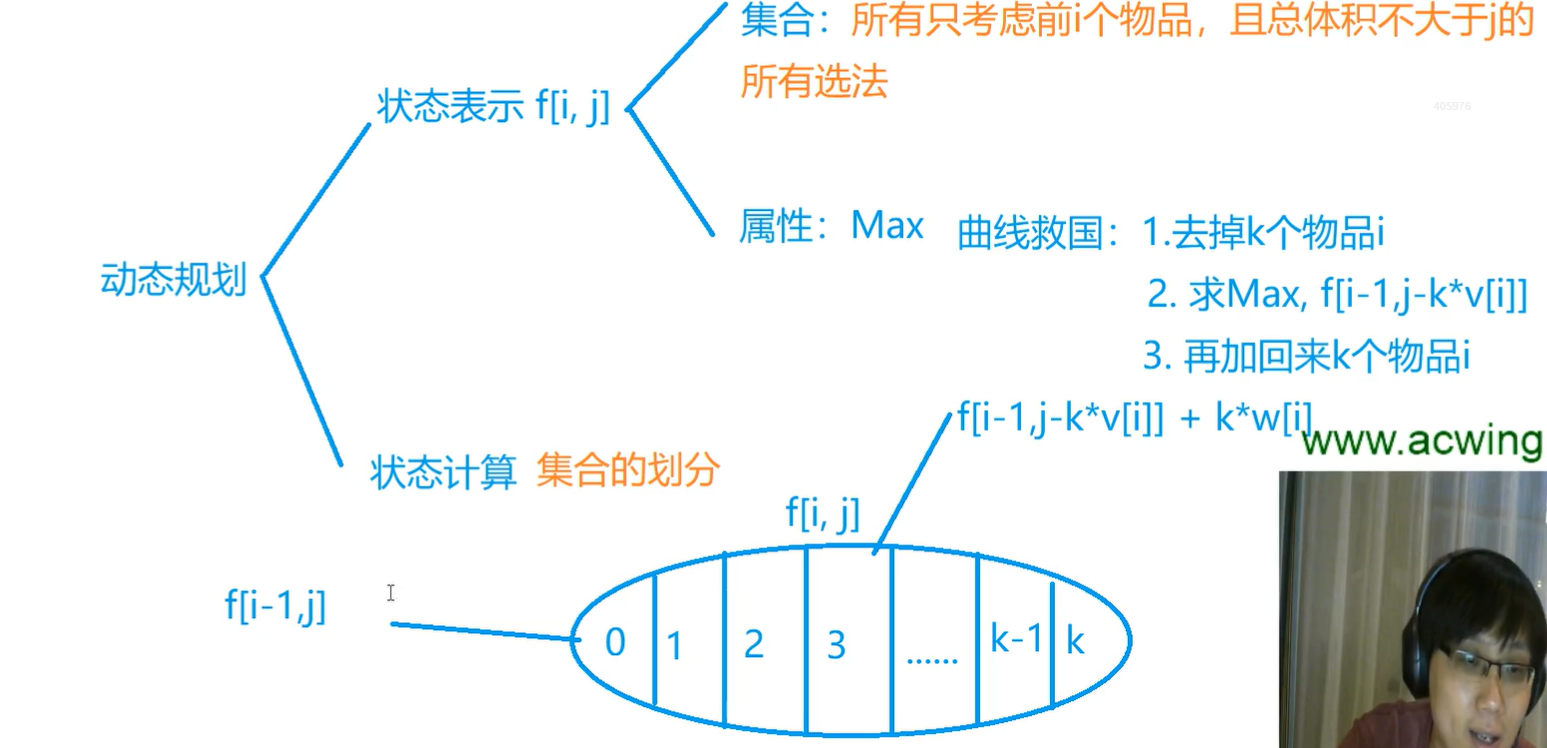
也就是我们在考虑状态计算的时候,将集合划分成,没有,有一个,有两个....
在此基础上我们的朴素代码可以写成
#include #include using namespace std;const int N=1010;int f[N][N];int v[N],w[N];int n,m;int main(){ cin>>n>>m; for(int i=1;i>v[i]>>w[i]; for(int i=1;i<=n;i++) { for(int j=0;j<=m;j++) { for(int k=0;k*v[i]<=j;k++) { f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]); } } } cout<<f[n][m]; return 0;}核心在三重循环上,完美对应集合划分
在此基础上我们需要进行优化


核心代码如下
for(int i=1;i<=n;i++) { for(int j=0;j=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]); } }在此基础上我们是否可以像0-1背包那样优化成一维的呢?,可以,但是思路与0-1背包不同
![]()
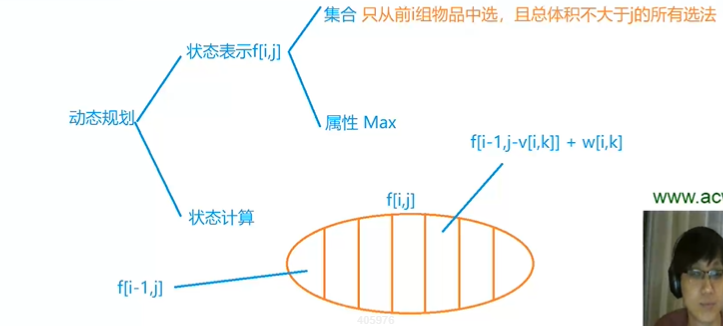
由公式可得到,f[i][j]并不是全由i-1层得到,相反,我们必须先得到i层元素,还是和原来一样,如果j<v[i]不需要变化,只需要继承上一层,所以我们的遍历应该是从前往后遍历
我们拿0-1背包的图来看看

v[i]前面的不用管,j从v[i]开始,当遍历到后面时,j-v已经被修改过了变成了第i层的元素,而正在遍历还没修改的j号元素就是[i-1][j]
所以可以进一步优化为
for(int i=1;i<=n;i++){ for(int j=v[i];j<=m;j++) { f[j]=max(f[j],f[j-v[i]]+w[i]); }}优化为一维数组的完整代码
#include #include using namespace std;const int N=1010;int f[N];int v[N],w[N];int n,m;int main(){ cin>>n>>m; for(int i=1;i>v[i]>>w[i]; for(int i=1;i<=n;i++){ for(int j=v[i];j<=m;j++) { f[j]=max(f[j],f[j-v[i]]+w[i]); }} cout<<f[m]; return 0;}多重背包问题
AcWing 4. 多重背包问题 - AcWing
在完全背包的基础上,物品有了个数限制
朴素算法很简单,就是在完全背包的暴力算法基础上进行的
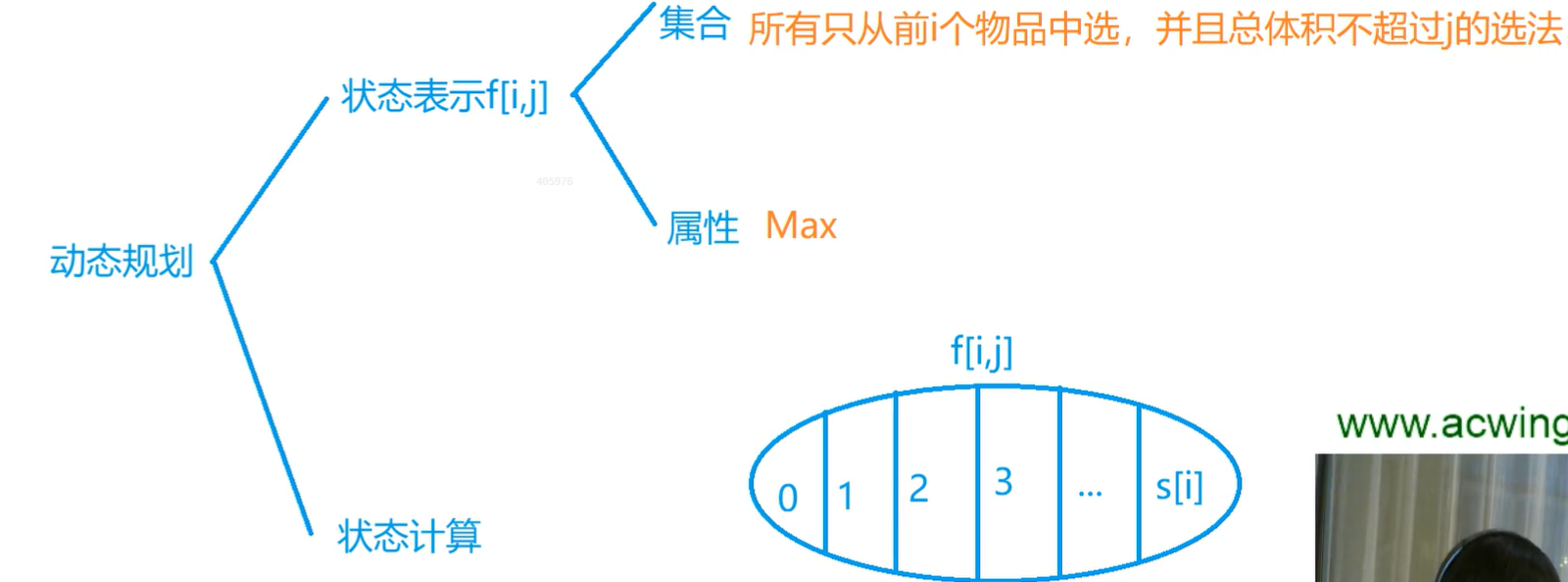
代码仅仅比完全背包的暴力dp多了一个判断
#include #include const int N=110;using namespace std;int s[N],v[N],w[N];int n,m;int f[N][N]; int main(){ cin>>n>>m; for(int i=1;i>v[i]>>w[i]>>s[i]; } for(int i=1;i<=n;i++) for(int j=0;j<=m;j++) { for(int k=0;k*v[i]<=j&&k<=s[i];k++){ f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k); } } cout<<f[n][m]; return 0;}这里我们是不能用f[i][j]和f[i][j-v]之间的关系来简化方程的,因为引入了s[i],所以我们不能像上面那样优化,我们采取优化的方式为二进制优化
二进制优化的多重背包问题
将多重背包问题转化成0-1背包问题
5. 多重背包问题 II - AcWing题库
我们知道,0-1背包是可以优化到一维的,对于多重背包而言,每个物品有s[i]个,如果从完全背包的角度理解,可以轻松写出暴力代码,但是无法优化三重循环,那如果从0-1背包的角度理解呢,

为什么是这样拆分,而不是直接用二进制呢,假设有50个物品,我们将其装到n个箱子里,要确保的是,我们通过取出不同的箱子组合,得到的值是映射在0到50里的,也就是说我们按照2进制的思想可以映射到 0到2的k次方-1,可以包含1到50但显然无法完全符合条件,我们只需要将最后一个最大的2进制(箱子),转换为剩余的数,比如50
1 2 4 8 16 19
1 2 4 8 16 32
我们需要按照上面的方法进行划分
代码如下
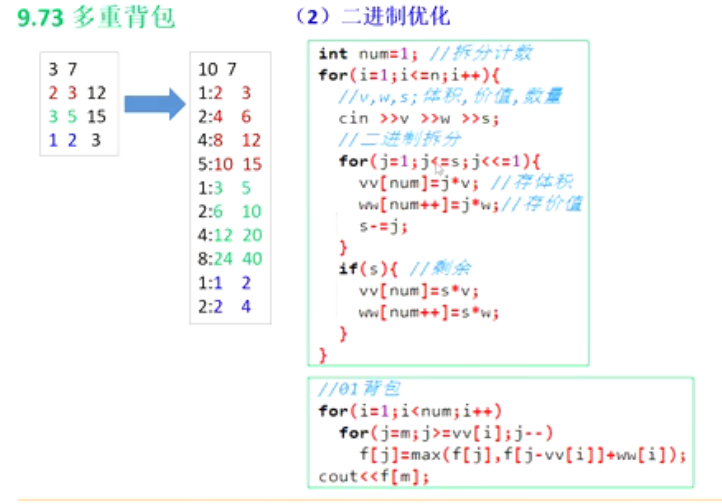
#include using namespace std;int v[12010],w[12010];int cnt=1;int f[2010];int n,m;int main(){ cin>>n>>m; while(n--){ int a,b,c; cin>>a>>b>>c; for(int i=1;i<=c;i<<=1) { v[cnt]=i*a; w[cnt]=b*i; cnt++; c-=i; } if(c) { v[cnt]=c*a; w[cnt++]=c*b; } } for(int i=1;i=v[i];j--) { f[j]=max(f[j],f[j-v[i]]+w[i]); } cout<<f[m]; return 0;}注意是<<=或者写成*=2
分组背包问题
集合划分为选第i组的哪一个物品
#include using namespace std;const int N=110;int n,m;int s[N],v[N][N],w[N][N];int f[N][N];int main(){ cin>>n>>m; for(int i=1;i>s[i]; for(int j=1;j>v[i][j]>>w[i][j]; } }for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){ f[i][j]=f[i-1][j]; for(int x=1;x=v[i][x])f[i][j]=max(f[i][j],f[i-1][j-v[i][x]]+w[i][x]); } }cout<<f[n][m]; return 0;}


