【论文阅读笔记】TransparentGS：当高斯溅射学会“看穿”玻璃，如何攻克透明物体重建难题？_gaussian splatting 透明玻璃

文章目录

• TransparentGS: Fast Inverse Rendering of Transparent Objects with Gaussians
• • Info
  • Abstract
  • Introduction
  • Method
  • • 预备知识
    • • 3D GS的概念不再赘述
      • 渲染方程
    • 透明高斯
    • Gaussian Light Field Probes
    • 多阶段重建
  • 实验
  • • 结果和评估
  • 消融实验
  • 应用
  • • 讨论和限制
  • 结论

TransparentGS: Fast Inverse Rendering of Transparent Objects with Gaussians

Info

会议 【TOG 2025】

作者 南京大学、南开大学、浙江大学

Project地址 https://letianhuang.github.io/transparentgs/

Abstract

本文聚焦于使用 3D GS 实现反射和折射场景的新视角合成，提出了一种名为 TransparentGS 的方法。它是一个基于3D-GS、用于快速重建透明物体的逆向渲染管线。主要贡献包含三个方面：

• 设计了一种高效的透明物体表示方法：我们设计了“透明高斯基元”（transparent Gaussian primitives），它通过一种“延迟折射”（deferred refraction）策略，实现了对高光折射的模拟。
• 统一环境光与邻近内容的编码：我们利用“高斯光场探针”（Gaussian light field probes, GaussProbe），在一个统一的框架内，同时对环境光和邻近物体内容进行编码。
• 提出了一种减少视差误差的算法：我们提出了一种名为“基于深度的迭代式探针查询”（depth-based iterative probes query, IterQuery）的算法，以减少我们这种基于探针框架中的视差（parallax）错误。

Introduction

从不同视角的多张二维图像重建三维场景并合成新视角一直是计算机图形学和视觉中的一项长期任务。随着深度学习的出现，神经辐射场（NeRF）及其变体在解决这一任务中引领了趋势，它们通过使用隐式场的体积渲染实现了照片级真实感的视觉质量。最近，随着对实时渲染需求的不断增加，三维高斯溅射（3D-GS）提供了一种更高效的显式表示，能够通过将辐射场建模为三维高斯原语来实现实时渲染。

然而，直到现在，在任意光照条件下重建透明物体并实现实时新视角合成仍然具有挑战性。这一挑战源于透明物体在不同视点下频繁出现的变化，主要由于光线穿过材料时反射和折射的复杂相互作用。因此，NeRF中的具有方向编码的多层感知机（MLP）和3D-GS中的球面谐波函数（SH）在准确建模镜面反射和折射方面都面临困难。

目前，针对透明物体的最有效重构方法是基于隐式神经表示的 [Bemana et al. 2022; Gao et al. 2023; Li et al. 2020; Sun et al. 2024]。然而，这些方法以训练过程中的显著计算开销而闻名，并且如表1所述，它们也不支持实时渲染。基于3D-GS的方法在3D重构和新视角合成方面提供了高效率 [Wu et al. 2024b]，但现有方法各自存在局限性。特别是这些方法 [Jiang et al. 2024; Ye et al. 2024] 原本是为反射场景设计的，无法轻易应用于透明物体。当透明物体周围有附近物体时，困难程度进一步加大。由于基于光栅化的公式，3D-GS受到理想针孔相机的限制，缺乏对折射和相互反射等次级光线效应的支持 [Huang et al. 2024; Moenne-Loccoz et al. 2024]。

在本文中，我们提出了TransparentGS，一个新颖的逆向渲染框架，该框架基于3D-GS，能够高效地管理在各种光照和视角条件下的透明物体，同时支持与邻近内容的折射和相互反射。在此框架中，透明物体由透明高斯原语建模，这些原语明确编码了3D高斯中的几何和材料属性。这些新原语便于集成到专门的物理基础延迟渲染流水线中，从而实现网格和高斯的整合，以处理次级光线效果。为了处理场景中的环境光和邻近内容，我们引入了高斯光场探针（GaussProbe），通过在透明物体周围放置稀疏的缓存集来捕捉每个透明物体的局部光场。这些探针可以基于最佳投影策略快速烘焙和更新 [Huang et al. 2024]。为了解决探针固有的视差问题并增强折射/相互反射的细节，我们设计了一种基于深度的迭代探针查询算法（IterQuery），该算法在经过几次迭代后能实现可信的结果。与之前的工作相比，我们的新框架具有几个优势，如表1所列。特别地，我们在一小时内实现了透明物体的快速逆向渲染及次级光线效果，能够实时合成透明场景的新视图以及复杂的次级光线效果，如图1所示。

与之前的工作相比，我们的新框架有几个优点，如表1所示。特别是，我们在一小时内实现了首个快速反向渲染，能够处理透明物体的次级光线效应，从而实现透明场景和复杂次级光线效应的实时新视角合成，如图1所示。总之，本工作的贡献如下：

• 我们设计了一种高效的透明物体表示，透明高斯原语，使得通过延迟折射策略实现镜面折射成为可能。
• 我们利用高斯光场探针（GaussProbe）在统一框架内编码环境光和附近内容。
• 我们提出了一种基于深度的迭代探针查询算法（IterQuery），以减轻我们基于探针的框架中的视差误差。

Method

在本节中，我们介绍了我们的方法TransparentGS，旨在快速逆渲染透明物体。如图2所示，我们的TransparentGS由两部分组成。第一部分是透明物体的表示，透明高斯原语，包含遵循3D高斯点云（3D-GS）[Kerbl et al. 2023]的形状属性。为了增强折射的表示能力，我们通过额外属性扩展了原语，包括法线和双向散射分布函数（BSDF）[Bartell et al. 1981]的参数。为了利用原语渲染详细的高光折射，我们采用了一种延迟折射方法。第二部分是我们提出的高斯光场探针（GaussProbe），它不仅表示类似于环境贴图的环境光，还表示来自附近内容的间接光。为了消除视差问题，我们开发了一种基于深度的迭代探针查询（IterQuery）算法，专门用于高斯光场探针。

预备知识

3D GS的概念不再赘述

渲染方程

L = ∫ Ω L i n ( x , ω i n ) f ( x , ω , ω i n ) ∣ ω i n ⋅ n ∣ d ω i n . (3) L = \\int_{\\Omega} L_{in} (\\mathbf{x}, \\omega_{in}) f (\\mathbf{x}, \\omega, \\omega_{in}) |\\omega_{in} \\cdot \\mathbf{n}| d\\omega_{in}. \\tag 3 L=∫Ω​Lin​(x,ωin​)f(x,ω,ωin​)∣ωin​⋅n∣dωin​.(3)

双向散射分布函数，𝐿 是阴影结果，𝐿in 是入射辐射，n 是表面法线，𝜔 和 𝜔 i n 𝜔_{in} 𝜔in​ 分别是出射方向和入射方向。𝑓 表示表面点 x 的双向散射分布函数（BSDF），可以进一步细分为双向反射分布函数（BRDF）和双向透射分布函数（BTDF）。

透明高斯

在3D-GS中，球面谐波 [Kerbl et al. 2023] 难以准确捕捉镜面反射和折射中外观的高频变化，这导致了过拟合，从而在新视角中造成退化，或者结果高度模糊。为了解决这个问题，我们提出了一种新的表示，透明高斯原语，它涉及基于物理的渲染流水线，而不是直接计算球面谐波。参数化。如图2所示，我们将表面几何体参数化为法线n，将表面材料参数化为粗糙度𝜌和金属度𝑚。对于透明物体，考虑表面的传输和折射是至关重要的。因此，我们利用两个额外的材料参数：透明度𝑡和折射率(IOR) 𝜂。透明度𝑡用于在不透明材料和透明材料之间进行插值。此外，为了保持高运行性能，我们保留了原始3D-GS [Kerbl et al. 2023] 的形状参数用于𝛼混合和光栅化。

不透明度属性在三维生成系统（3D-GS）中发挥着关键作用，即使对于不透明物体，因为三维生成系统依赖于体积𝛼混合。对于透明物体，仅仅使用较低的不透明度来表示透明性将无法准确表现其表面，这反过来又使得计算折射和反射变得困难。因此，我们引入了一个额外的参数𝑡，以便于在计算机图形学中的应用，例如材料编辑。

表面反射和折射。在本文中，我们通过两个分离的BSDF明确表示表面反射和折射：
f = ( 1 − t ) f r + t f t f = (1 - t)f_r + tf_t f=(1−t)fr​+tft​
其中 𝑓 𝑟 𝑓_𝑟 fr​ 表示双向反射分布函数（BRDF）， 𝑓 𝑡 𝑓_𝑡 ft​ 表示双向透射分布函数（BTDF）。对于不透明材料，当 𝑡 = 0 时，我们遵循 Cook-Torrance 模型 [1981]。而对于金属或透明物体的反射成分，当 $𝜌=0$ 时，我们将其视为完美镜面反射：
f r = F δ ( ω − ω r ) ∣ ω i n ⋅ n ∣, with ω r = 2 ( ω i n⋅ n ) n − ω i n f_r = F \\frac{\\delta(\\omega - \\omega_r)}{|\\omega_{in} \\cdot \\mathbf{n}|}, \\quad \\text{with} \\quad \\omega_r = 2(\\omega_{in} \\cdot \\mathbf{n})\\mathbf{n} - \\omega_{in} fr​=F∣ωin​⋅n∣δ(ω−ωr​)​,withωr​=2(ωin​⋅n)n−ωin​
其中 𝜔 𝑟 𝜔_𝑟 𝜔r​ 表示分析反射方向，𝛿 表示 Dirac Delta函数，而 Fresnel 项 𝐹 可以使用 Schlick 近似 [Schlick 1994] 进行近似。同样，对于透明物体的透射成分，当 𝜌 = 0 时，我们仅考虑完美的镜面折射：

f t = ( 1 − F ) δ ( ω − ω t ) ∣ ω i n ⋅ n ∣ (6) f_t = (1 - F) \\frac{\\delta(\\omega - \\omega_t)}{|\\omega_{in} \\cdot \\mathbf{n}|} \\tag 6 ft​=(1−F)∣ωin​⋅n∣δ(ω−ωt​)​(6)

其中 𝜔 𝑡 𝜔_𝑡 𝜔t​ 指的是折射方向。如图 2 所示，解析的折射方向是根据斯涅尔定律获得的。

延迟折射 使用3D-GS进行反向渲染的一个关键方面是着色方案。通常，着色策略可以分为两种类型：前向着色和延迟着色。“前向”指的是首先进行着色，然后进行𝛼混合，而“延迟”则相反。先前的研究强调了操作顺序对镜面反射的影响。受到一些关于延迟反射的研究启发 [Wu et al. 2024a; Ye et al. 2024]，我们探讨了在处理镜面折射时采用延迟着色的可能性。具体而言，我们使用公式（3）和公式（6）推导透射颜色：

L t = ∫ Ω L i n ( x , ω i n ) ( 1 – F ) δ ( ω – ω t ) d ω i n = ( 1 – F ) L i n ( x , ω t ) . (7) L_t = \\int_{\\Omega} L_{in} (\\mathbf{x}, \\omega_{in}) (1 – F) \\delta (\\omega – \\omega_t) d\\omega_{in} = (1 – F) L_{in} (\\mathbf{x}, \\omega_t). \\tag 7 Lt​=∫Ω​Lin​(x,ωin​)(1–F)δ(ω–ωt​)dωin​=(1–F)Lin​(x,ωt​).(7)

由于𝛼混合是一种线性的操作，而方程（7）相对于法线n并不是线性的，因此操作顺序对折射有显著影响。前向折射对高斯的阴影结果进行了平均。与前向折射相比，延迟阴影在捕捉具有镜面折射的透明物体方面更为擅长，因为它对光照进行了单次采样，如图3所示。在我们的延迟折射策略中（见图2），我们采用了一种基于点的𝛼混合方法，类似于方程（2），以聚合所有由基元携带的反射和折射相关属性。例如，带有α加权的法线的计算公式为：

N = ∑ i = 1 N T i α i n i (8) \\mathcal{N}=\\sum_{i=1}^{N} T_{i}\\alpha_{i}\\mathbf{n}_{i} \\tag 8 N=i=1∑N​Ti​αi​ni​(8)

此外，与基于环境光的反射相比，我们还需要整合光线的入射点以进行折射和反射。然而，仅仅整合原始图形的中心𝝁会忽略它们的各向异性，从而导致误差。我们采用了一种更精确的策略来计算入射点。考虑到原点 o c a m o_{cam} ocam​和视向方向 v= 𝜔 i n v = 𝜔_{in} v=𝜔in​的主光线 o c a m +𝜏v o_{cam} + 𝜏v ocam​+𝜏v，光线上的高斯值可以表示为距离𝜏的函数：

G ( τ ) = exp ⁡ ( − 1 2 ( o cam + τ v − μ ) ⊤ Σ − 1 ( o cam + τ v − μ ) ) (9) \\mathcal{G}(\\tau)=\\exp\\left(-\\frac{1}{2}\\left(\\mathbf{o}_{\\text{cam}}+\\tau\\mathbf{v}-\\boldsymbol{\\mu}\\right)^{\\top}\\Sigma^{-1}\\left(\\mathbf{o}_{\\text{cam}}+\\tau\\mathbf{v}-\\boldsymbol{\\mu}\\right)\\right) \\tag{9} G(τ)=exp(−21​(ocam​+τv−μ)⊤Σ−1(ocam​+τv−μ))(9)

公式解释
含义: 这是一个以 $\tau$ 为参数的指数函数，表示一个高斯核（Gaussian kernel）。它计算在方向 $\mathbf{v}$ 上偏移 $\tau$ 后的点 o cam +τv \\mathbf{o}_{\\text{cam}} + \\tau\\mathbf{v} ocam​+τv 到均值点 $\mathbf{\mu }$ 的马氏距离（Mahalanobis distance），再通过指数映射为概率密度或权重值。当 $\mathcal{G}(\tau )$ 越大时，表示 o cam +τv \\mathbf{o}_{\\text{cam}} + \\tau\\mathbf{v} ocam​+τv 越接近 $\mathbf{\mu }$ 在高斯分布下的“相似度”。
此公式常用于求解优化问题（如寻找使 $\mathcal{G}(\tau )$ 最大化的 $\tau$），例如在最大似然估计或光线-物体交点检测中。
指数函数 $\exp (\cdot )$ 是单调递增的，因此最大化 $\mathcal{G}(\tau )$ 等价于最小化内部二次型：

目标: 求 τ ∗ =arg⁡ min ⁡ τ f(τ) \\tau^* = \\arg\\min_{\\tau} f(\\tau) τ∗=argminτ​f(τ)。
求导法求解:
对 $f(\tau )$ 求导（假设 Σ − 1 \\Sigma^{-1} Σ−1 对称正定）：
d fd τ =2 v ⊤ Σ − 1 ( o cam +τv−μ) \\frac{df}{d\\tau} = 2\\mathbf{v}^{\\top} \\Sigma^{-1} (\\mathbf{o}_{\\text{cam}} + \\tau\\mathbf{v} - \\boldsymbol{\\mu}) dτdf​=2v⊤Σ−1(ocam​+τv−μ)

令导数为零得到关键点:
v ⊤ Σ − 1 ( o cam +τv−μ)=0 \\mathbf{v}^{\\top} \\Sigma^{-1} (\\mathbf{o}_{\\text{cam}} + \\tau\\mathbf{v} - \\boldsymbol{\\mu}) = 0 v⊤Σ−1(ocam​+τv−μ)=0

解出 $\tau$:
τ ∗ = v ⊤ Σ − 1 ( μ − o cam ) v ⊤ Σ − 1 v \\tau^* = \\frac{\\mathbf{v}^{\\top} \\Sigma^{-1} (\\boldsymbol{\\mu} - \\mathbf{o}_{\\text{cam}})}{\\mathbf{v}^{\\top} \\Sigma^{-1} \\mathbf{v}} τ∗=v⊤Σ−1vv⊤Σ−1(μ−ocam​)​
这是 $f(\tau )$ 的最小值点（从而 $\mathcal{G}(\tau )$ 的最大值点）。
优化算法替代：
如果协方差 $\Sigma$ 是病态的（不易求逆），可使用数值方法：
梯度下降: 以初始 τ 0 \\tau_0 τ0​ 开始，迭代更新 τ k + 1 = τ k −η d fd τ \\tau_{k+1} = \\tau_k - \\eta \\frac{df}{d\\tau} τk+1​=τk​−ηdτdf​（其中 $\eta$ 为学习率）。
牛顿法: 适用于更高精度，利用二阶导信息加速收敛。
验证: 计算二次型 f( τ ∗ ) f(\\tau^*) f(τ∗) 的值，确保其为全局最小（马氏距离在凸优化中单峰）。

我们通过分析计算该函数的最大值，并沿着光线聚合高斯的响应，具体如下：

χ = o cam  + v ∑ i = 1N T i α i arg ⁡ max ⁡τ G i ( τ ) arg ⁡ max ⁡τ G i ( τ ) = ( μ i − o cam  ) ⊤ Σ − 1 v v ⊤ Σ − 1 v (10) \\begin{array}{l} \\chi = \\mathbf{o}_{\\text{cam }} + \\mathbf{v} \\sum_{i=1}^{N} T_{i} \\alpha_{i} \\arg \\max _{\\tau} \\mathcal{G}_{i}(\\tau) \\\\ \\arg \\max _{\\tau} \\mathcal{G}_{i}(\\tau) = \\dfrac{\\left(\\boldsymbol{\\mu}_{i}-\\mathbf{o}_{\\text{cam }}\\right)^{\\top} \\Sigma^{-1} \\mathbf{v}}{\\mathbf{v}^{\\top} \\Sigma^{-1} \\mathbf{v}} \\end{array} \\tag{10} χ=ocam ​+v∑i=1N​Ti​αi​argmaxτ​Gi​(τ)argmaxτ​Gi​(τ)=v⊤Σ−1v(μi​−ocam ​)⊤Σ−1v​​(10)

其中，$\chi$ 是 alpha 加权的击中点， G 𝑖 G_𝑖 Gi​ 表示沿光线的第 𝑖 个原始体。公式 (10) 考虑了透明高斯原始体的各向异性，其中不同的像素对应于不同的击中点。折射光线 𝜔 𝑡 𝜔_𝑡 𝜔t​ 和反射光线 𝜔 𝑟 𝜔_𝑟 𝜔r​ 是使用存储在几何缓冲区（G-buffer）中的这些聚合属性计算的，以便进行后续查询。

处理彩色透明物体。我们的方法可以很容易地扩展到处理彩色透明物体中的吸收。我们只需通过以下方式修改公式（7）：

L t = ( 1 − F ) L in ( x , ω t ) e − σ ( λ ) d (11) L_{t} = (1 - F)L_{\\text{in}}\\left(\\mathbf{x},\\omega_{t}\\right) e^{-\\sigma(\\lambda) d} \\tag {11} Lt​=(1−F)Lin​(x,ωt​)e−σ(λ)d(11)

其中，$𝜎(\cdot )$是材料的吸收系数，𝜆是光的波长，𝑑表示光在材料中传播的路径长度。我们使用加权基色 ∑ 𝑖 = 1 𝑁 𝑇 𝑖 𝛼 𝑖 b i \\sum^{𝑁}_{𝑖=1} 𝑇_𝑖 𝛼_𝑖 b_i ∑i=1N​Ti​𝛼i​bi​来近似指数项（透射率），其中 b 𝑖 b_𝑖 bi​是编码在每个透明高斯基元中的可优化参数。得益于这一设计，我们的方法有效地将折射项与透明物体的固有颜色解耦，这是其他方法难以处理的挑战。

Gaussian Light Field Probes

入射光的表示选择显著影响反向渲染。仅使用具有两个自由度的环境地图来表示来自附近内容的间接光会导致严重的视差问题。为了克服普通3D-GS [Kerbl et al. 2023] 无法处理的不相干光线的挑战，我们提出了一种新颖的光表示：高斯光场探针（GaussProbe）。本节中的重要符号在表2中展示。

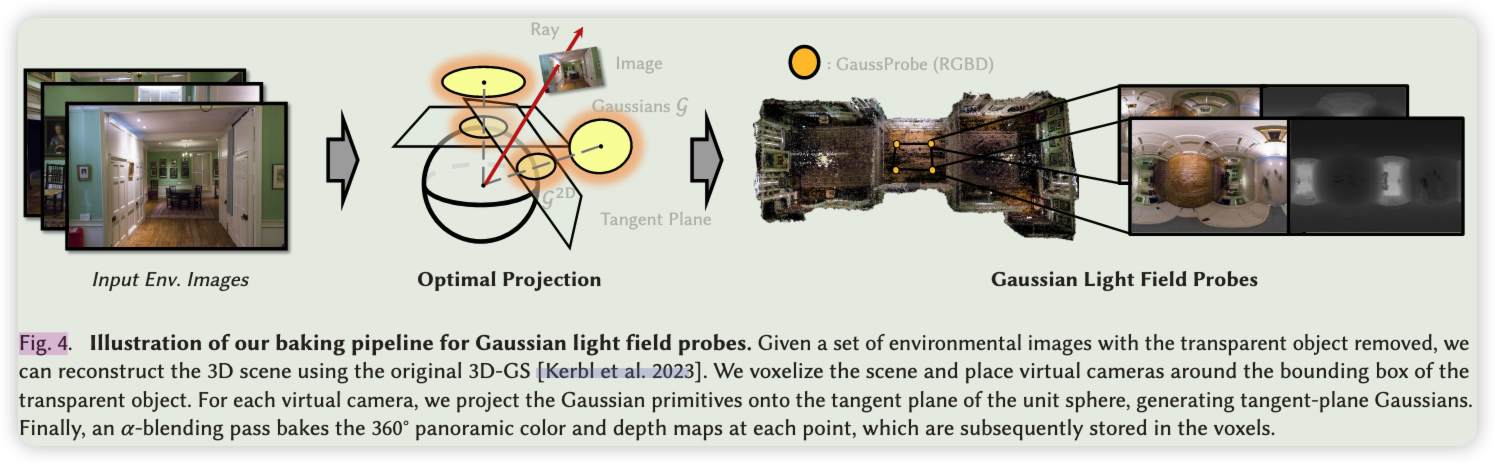
烘焙高斯光场探针 在重建透明物体之前，我们首先烘焙高斯光场探针。如图4所示，我们首先通过普通3D-GS [Kerbl et al. 2023] 重建环境。然后我们对场景进行体素化，并在透明物体的包围盒周围的体素中放置探针。对于每个探针，我们遵循最佳投影 [Huang et al. 2024] 在虚拟相机的情景下渲染全景图像。具体来说，我们将高斯原件投影到单位球对应的切平面上，使用投影函数𝜑而不是图像平面。相应的局部仿射近似雅可比矩阵经过修改。

J = 1 ( μ x 2 + μ y 2 + μ z 2 ) 3 2 [ μ y 2 + μ z 2 − μ x μ y − μ x μ z − μ x μ y μ x 2 + μ z 2 − μ y μ z − μ x μ z − μ y μ z μ x 2 + μ y 2 ] (12) \\mathbf{J} = \\frac{1}{(\\mu_x^2 + \\mu_y^2 + \\mu_z^2)^{\\frac{3}{2}}} \\begin{bmatrix} \\mu_y^2 + \\mu_z^2 & -\\mu_x\\mu_y & -\\mu_x\\mu_z \\\\ -\\mu_x\\mu_y & \\mu_x^2 + \\mu_z^2 & -\\mu_y\\mu_z \\\\ -\\mu_x\\mu_z & -\\mu_y\\mu_z & \\mu_x^2 + \\mu_y^2 \\end{bmatrix} \\tag{12} J=(μx2​+μy2​+μz2​)23​1​ ​μy2​+μz2​−μx​μy​−μx​μz​​−μx​μy​μx2​+μz2​−μy​μz​​−μx​μz​−μy​μz​μx2​+μy2​​ ​(12)

其中 𝝁^′=[𝜇_𝑥 , 𝜇_𝑦, 𝜇_𝑧]^⊤ 表示相机空间中 3D 高斯的位置。

对于图像上的一个像素 (𝑢, 𝑣)，投射一条光线并计算与切平面的交点：

常规图像 → 球面投影 用于360°全景图制作

x 2 D = φ ( [ sin ⁡ ( π ( − W + 2 u ) W ) cos ⁡ ( π ( − H / 2 + v ) H )sin ⁡ ( π ( − H / 2 + v ) H )cos ⁡ ( π ( − H / 2 + v ) H ) cos ⁡ ( π ( − W + 2 u ) W ) ] ) (13) \\mathbf{x}_{2D} = \\varphi \\left( \\begin{bmatrix} \\sin \\left( \\frac{\\pi(-W + 2u)}{W} \\right) \\cos \\left( \\frac{\\pi(-H/2 + v)}{H} \\right) \\\\ \\sin \\left( \\frac{\\pi(-H/2 + v)}{H} \\right) \\\\ \\cos \\left( \\frac{\\pi(-H/2 + v)}{H} \\right) \\cos \\left( \\frac{\\pi(-W + 2u)}{W} \\right) \\end{bmatrix} \\right) \\tag{13} x2D​=φ ​ ​sin(Wπ(−W+2u)​)cos(Hπ(−H/2+v)​)sin(Hπ(−H/2+v)​)cos(Hπ(−H/2+v)​)cos(Wπ(−W+2u)​)​ ​ ​(13)

其中 𝐻 和 𝑊 表示全景的分辨率。在 𝛼 混合过程中，我们将公式 (2) 中的 G 2 D G_{2D} G2D​ 替换为 x 2 D x_{2D} x2D​ 处切平面高斯的值。此外，为了渲染全景的深度，我们使用原始物体到相机中心的欧氏距离替代 𝜇 𝑧 𝜇_𝑧 𝜇z​。最后，位于位置 p 𝑖 p_𝑖 pi​ 的第 𝑖 个探针存储了颜色全景 Φ 和深度全景 Θ，从而分别通过方向 d 𝑖 d_𝑖 di​ 进行颜色查询 c 𝑖 c_𝑖 ci​ 和深度查询 t 𝑖 t_𝑖 ti​。

c 𝑖 , 𝑡 𝑖 = Φ ( p 𝑖 , d 𝑖 ) , Θ ( p 𝑖 , d 𝑖 ) . c_𝑖 , 𝑡_𝑖 = Φ (p_𝑖 , d_𝑖 ) , Θ (p_𝑖 , d_𝑖 ) . ci​,ti​=Φ(pi​,di​),Θ(pi​,di​).

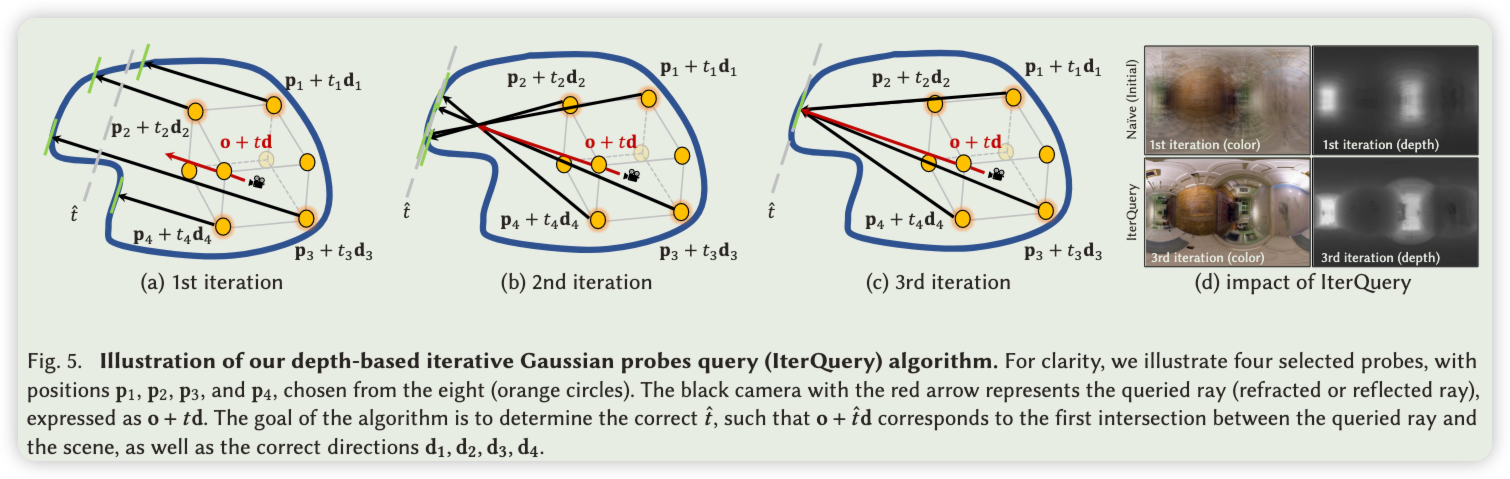
基于深度的迭代探测查询。在进行逆向渲染时计算折射或反射光线时，我们应该根据给定的光线进行探测查询。设 o 和 d 分别表示查询光线的原点和方向。我们还将 p 𝑖 p_𝑖 pi​ 和 d 𝑖 d_𝑖 di​ 分别表示第 𝑖 个探测器的位置和方向。图 5(d) 说明了在相同方向 d 𝑖 = d d_𝑖 = d di​=d 上天真地查询 𝐾 个探测器并对结果进行平均会导致由于探测器之间的视差而产生过度模糊。为了更好地捕捉镜面反射和折射中的细节，我们提出了一种基于深度的迭代探测查询（IterQuery）算法，专为我们的烘焙高斯探测器定制。

如图5所示，我们将探针 d 𝑖 d_𝑖 di​的方向初始化为查询光线d的方向：

d i : = d d_i:=d di​:=d

然后我们查询深度 𝑡 𝑖 𝑡_𝑖 ti​，以获得第 𝑖 个探针与环境的交点 p 𝑖 + 𝑡 𝑖 d𝑖 p_𝑖 +𝑡_𝑖 d𝑖 pi​+ti​di：

$$ti=\Theta (pi,di)\text{\hspace{1em}(16)}$$

投影到查询光线上的深度图的三线性插值由下式给出：
t ^ = ∑ ︁ 𝑖 = 1 k 𝑤 𝑖 ( ( p 𝑖 + 𝑡 𝑖 d 𝑖 − o ) ⋅ d ) (17) \\hat t = ∑︁^k_{𝑖=1}𝑤_𝑖 ((p_𝑖 + 𝑡_𝑖 d_𝑖 − o) · d) \\tag {17} t^=∑︁i=1k​wi​((pi​+ti​di​−o)⋅d)(17) 其中 · 表示向量的点积， 𝑤 𝑖 𝑤_𝑖 wi​ 是插值权重。然后，使用以下公式更新

$$di：di:=o+ˆtd-pio+ˆtd-pi\text{\hspace{1em}(18)}$$

然后，更新后的 d 𝑖 d_𝑖 di​ 以与前一次迭代相同的方式进行查询。从探针查询的深度（绿色虚线）对应于 3D 场景表面上的一个点，而 {\\hat t} 对应于要查询的光线上的一个点（灰色虚线）。因此，当 {\\hat t}保持不变时，待查询的光线应与场景相交。我们为 𝐾 = 1 的情况提供了一个简化的形式证明。由于收敛条件要求{\\hat t} 保持不变，我们可以同时求解方程（16）、方程（17）和方程（18），以推导出以下公式：

t ^ = ( p i +o + t ^ d − p i ∥ o + t ^ d − p i ∥ Θ ( p i , d i ) − o ) ⋅ d (19) \\hat{t}=\\left(\\mathbf{p}_{i}+\\frac{\\mathbf{o}+\\hat{t}\\mathbf{d}-\\mathbf{p}_{i}}{\\left\\|\\mathbf{o}+\\hat{t}\\mathbf{d}-\\mathbf{p}_{i}\\right\\|}\\Theta\\left(\\mathbf{p}_{i},\\mathbf{d}_{i}\\right)-\\mathbf{o}\\right)\\cdot\\mathbf{d} \\tag{19} t^=(pi​+ ​o+t^d−pi​ ​o+t^d−pi​​Θ(pi​,di​)−o)⋅d(19)

Θ ( p i , d i ) = t i = ∥ o + t ^ d − p i ∥ (20) \\Theta\\left(\\mathbf{p}_{i}, \\mathbf{d}_{i}\\right)=t_{i}=\\left\\|\\mathbf{o}+\\hat{t} \\mathbf{d}-\\mathbf{p}_{i}\\right\\| \\tag{20} Θ(pi​,di​)=ti​= ​o+t^d−pi​ ​(20)

o + t ^ d = p i + t i d i (21) \\mathbf{o}+\\hat{t} \\mathbf{d}=\\mathbf{p}_{i}+t_{i} \\mathbf{d}_{i} \\tag{21} o+t^d=pi​+ti​di​(21)

在迭代停止后，可以通过在公式(17)中将Θ替换为Φ来获得最终颜色。描述该算法的伪代码在列表1中提供。

理论上，IterQuery算法的时间复杂度为O (𝑇 𝐾𝑄)。𝑇、𝐾和𝑄分别表示总迭代次数、探测次数和查询射线的数量。所需的迭代次数受到探测次数𝐾和深度全景Θ的影响，我们将在实验部分进一步讨论这一点。与第一次迭代相比，我们的方法在效率和质量上都取得了显著的提升。

多阶段重建

与之前的研究相似[Liang et al. 2024; Liu et al. 2023]，我们采用多阶段重构策略来实现逆向渲染。第一阶段涉及环境重构和烘焙，其中烘焙的高斯探针用于几何和材料重构过程中的光计算。在第二阶段，我们利用透明高斯原语在基于物理的延迟渲染流水线中重构几何和材料。在此过程中，我们统一显式网格和GS以追踪二次光线，有效地精炼逆向渲染。

优化与损失 在多阶段重构过程中，我们对最终损失施加了一些正则项。对于normal的正则项，我们遵循之前的研究工作[Jiang et al. 2024; Wang et al. 2023]。

L normal = 1 − N ⋅ N ^ D \\mathcal{L}_\\text{normal} = 1 - \\mathcal{N} \\cdot \\hat{\\mathcal{N}}_D Lnormal​=1−N⋅N^D​

其中 N 表示渲染后的法线图， N D ^ \\hat {N_D} ND​^​ 是渲染后的深度图的梯度。我们还将掩码项和 D-SSIM 项纳入总损失 L，即：

L = ( 1 − λ 1 ) L 1 + λ 1L D-SSIM + λ 2L normal + λ 3L mask \\mathcal{L} = (1 - \\lambda_1) \\mathcal{L}_1 + \\lambda_1 \\mathcal{L}_\\text{D-SSIM} + \\lambda_2 \\mathcal{L}_\\text{normal} + \\lambda_3 \\mathcal{L}_\\text{mask} L=(1−λ1​)L1​+λ1​LD-SSIM​+λ2​Lnormal​+λ3​Lmask​

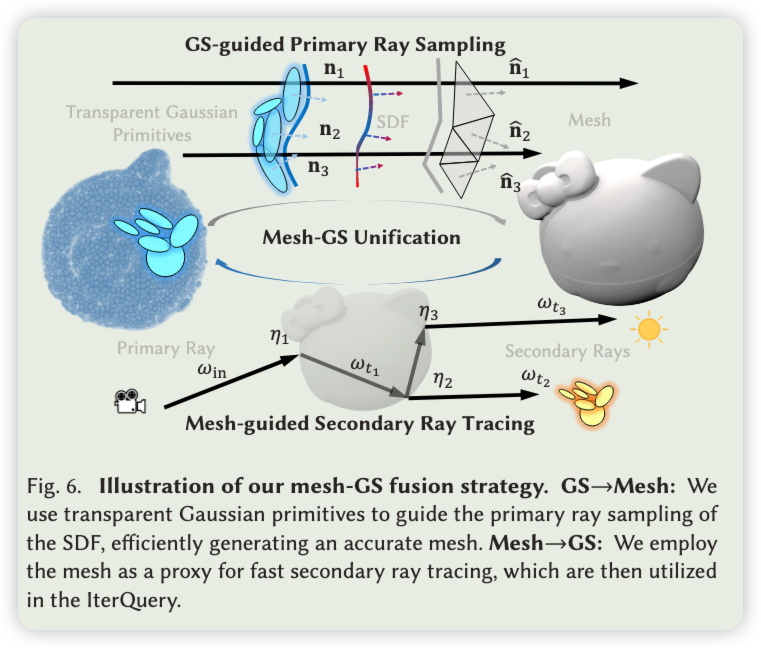
统一网格和高斯以处理次级光线效应 基于物理的折射在透明物体内部至少产生两次光线反弹。然而，基于光栅化的3D-GS [Kerbl et al. 2023] 无法处理次级光线。此外，已知前期基于NeRF的方法的第二次反弹光线行进成本较高 [Gao et al. 2023; Li et al. 2024]。虽然使用多层感知机预测折射方向 [Wang et al. 2023] 或光线 [Sun et al. 2024] 是有效的，但往往会导致细节丢失。受到高斯和SDF联合最优化 [Wu et al. 2024a; Yu et al. 2024] 以及SDF和网格统一 [Li et al. 2024] 的启发，我们统一透明高斯基元和网格以解决这一问题。如图6所示，在重构过程中，我们利用透明高斯基元渲染的命中点图X作为SDF的主光线采样的指导。
渲染的法线图N用于正则化梯度，从而提高估计的SDF的准确率。我们通过一个行进立方体算法从SDF场中提取显式网格[Lorensen和Cline 1987]。另一方面，我们将提取的网格作为代理，以高效追踪次级光线以进行后续的GaussProbe查询。我们的meshGS合一与SuGaR[Guédon和Lepetit 2024]有些相似，后者联合优化位于网格表面的网格和3D高斯。然而，我们的方法更侧重于利用3D-GS[Kerbl等，2023]的快速重构能力和网格在追踪次级光线中的效率，以进一步优化逆向渲染。

实验

实现细节：我们在3D-GS [Kerbl et al. 2023]的PyTorch框架基础上实现了我们的方法，使用Adam优化器 [Kingma 2014]。目前，在所有测试中，我们将损失设置为𝜆1 = 0.2，𝜆2 = 0.2，𝜆3 = 1。我们采用预训练的SAM2 [Kirillov et al. 2023; Ravi et al. 2024]，并通过GroundingDINO [Liu et al. 2024]指导进行3D场景分割，如图7所示。具体而言，通过输入文本提示，结合RGB图像，GroundingDINO可以为透明物体生成边界框。随后，这些边界框可以用作SAM2的框提示，以产生分割结果。这些结果作为高斯的正则化，促进3D场景分割。对于我们的高斯光场探针，我们将IterQuery算法的迭代次数设置为5，并经验性地将高斯探针的数量设置为8或64。对于所有基准方法，我们采用其官方实现。

数据集。我们在多个包含透明物体的数据集上进行评估，包括合成数据集和真实捕获的数据集。具体而言，我们从Bemana等人（2022）中获取了一个包含未知几何形状的折射物体的场景：玻璃，并自行捕获了6个场景：半球、苹果、海豚、企鹅、老鼠和鸟。使用智能手机拍摄 80～200views。

为了证明我们的方法能够处理来自不透明平面以外的邻近内容的间接光[高等，2023]，我们在透明物体周围放置了多个几何形状和纹理复杂的物体。此外，最后四个场景旨在验证我们对彩色透明物体的建模。为了定性比较我们的方法与其他方法的解耦和重构质量，我们使用Blender渲染了一个合成数据集，并生成了真实值图。我们将我们的方法与以下基线进行比较：

• GShader [Jiang et al. 2024]：基于3D-GS [Kerbl et al. 2023] 的光滑物体逆渲染框架。
• Eikonal [Bemana et al. 2022]：基于NeRF [Mildenhall et al. 2020] 的折射物体最先进（SOTA）新视角合成方法。
• NU-NeRF [Sun et al. 2024]：基于SDF [Ge et al. 2023; Wang et al. 2021] 的透明物体最先进重构方法。

我们不与 NEMTO [Wang et al. 2023] 和 Gao et al.[2023]，因为它们不适用于复杂的附近对象，并且 NUNeRF 已经与两者进行了比较。对于新视图和解耦反射、折射和基本颜色分量，我们提出了用三个标准指标测量的定量结果:峰值信噪比(PSNR)、结构相似性指数(SSIM) [Wang et al. 2004]和学习感知图像补丁相似度(LPIPS) [Zhang et al. 2018]。对于重建的法线图，我们使用度数 (MAE◦) 中的平均角误差来评估正常的重建精度。

结果和评估

定性比较。在图 8 和图 10 中，我们在真实捕获数据集上评估我们的方法。图 11 展示了对合成数据集的评估。可以看出，我们的方法能够有效且高效地重建透明物体。我们观察到，在某些情况下，即使是 NU-NeRF [Sun et al. 2024] 也有我们的方法避免的剩余伪影，例如 Glass 和 定性比较。在图 8 和图 10 中，我们在真实捕获数据集上评估我们的方法。

图 11 展示了对合成数据集的评估。可以看出，我们的方法能够有效且高效地重建透明物体。我们观察到，在某些情况下，即使是 NU-NeRF [Sun et al. 2024] 也有我们的方法避免的剩余伪影，例如 Glass 和 Kitty。其他方法 [Bemana et al.2022;Jiang et al. 2024]由于缺乏表面表示或折射建模，无法忠实地生成法线图。此外，我们的方法擅长捕捉镜面反射和折射的高频细节（例如，相互反射中的附近内容 - 在苹果 - 或折射 - 在鼠标中）。NU-NeRF [Sun et al. 2024]倾向于生成模糊的结果，由于其光表示，无法捕获详细的间接光。还应该注意的是，我们可以处理彩色透明对象并将折射项与固有颜色解耦。以前的方法要么无法处理吸收，要么产生纠缠的结果。我们提供了这些透明物体的表面网格重建结果，如图9所示。

我们的方法的详细中间结果如图12所示

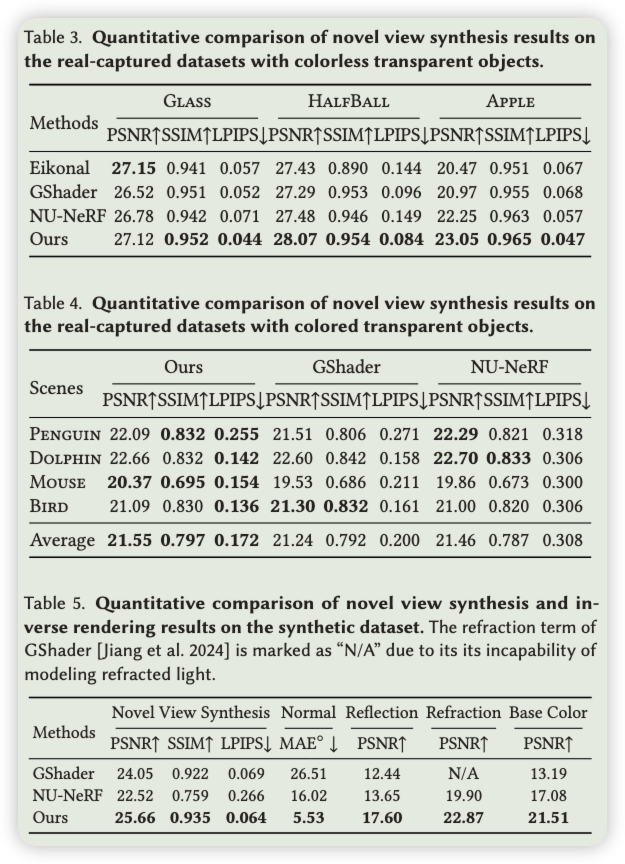
定量比较 Tab 3，4 显示了新视图合成结果在真实捕获数据集上的定量比较。在大多数场景中，我们超越了其他方法，特别是在LPIPS，并实现最高的平均指标。由于真实捕获的场景缺乏地面真实几何、材料和光，我们还在合成数据集上评估了我们的方法，如报告所示。

性能分析 一般来说，与 Eikonal [Bemana et al.2022] (22-24 小时) 和 NU-NeRF [Sun et al. 2024] (8,9 小时)，同时需要与 GShader [Jiang et al. 2024] (1 小时) 相当的训练时间。我们在几分钟内分割 3D 场景并烘焙 GaussProbe。在新颖的视图合成和重新渲染性能方面，运行时间取决于探针的数量、迭代次数和图像分辨率。对于 800 × 800 图像，对于 1 次迭代的单个探针，时间成本为 0.002 秒，对于 5 次迭代的 8 个探针，时间成本为 0.005 秒。我们的透明高斯基元，类似于其他基于 3D-GS 的方法 [Jiang et al. 2024; Ye et al. 2024]，能够实时渲染各种属性图以进行延迟着色。由于设计高效，我们的方法达到了 31-51 的帧速率，这明显快于现有的基于 NeRF 的作品：Eikonal [Bemana et al.2022] (0.03 FPS) 和 NU-NeRF [Sun et al. 2024] (0.016 FPS)。

消融实验

在本节中，我们进行了各种消融研究来验证我们方法中关键组件的影响。

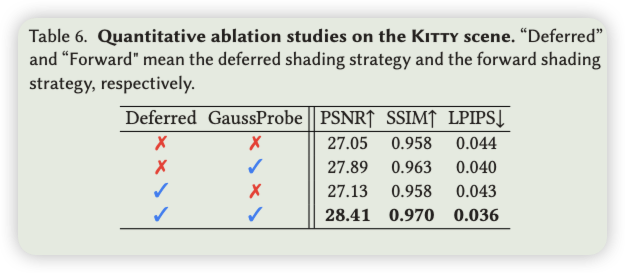
逆向渲染的消融研究 我们的方法对透明物体的插入渲染的关键组件是延迟折射策略和我们的高斯光场探针。因此，我们在 Kitty 场景的不同设置下提供了定量和定性的消融研究，如表 6 所示，如图13所示。可以观察到，前向阴影策略模糊了渲染结果中折射和反射的高频细节。在不使用探针的情况下，附近表中的折射光的整体颜色与地面真实情况有显著差异，但保留了来自“无限距离”的环境光的高频反射光。同时采用延迟阴影和高斯光场探针有效地结合了保留高频细节和确保准确查询方向的好处。指标进一步说明我们的完整模型达到了最高的质量。

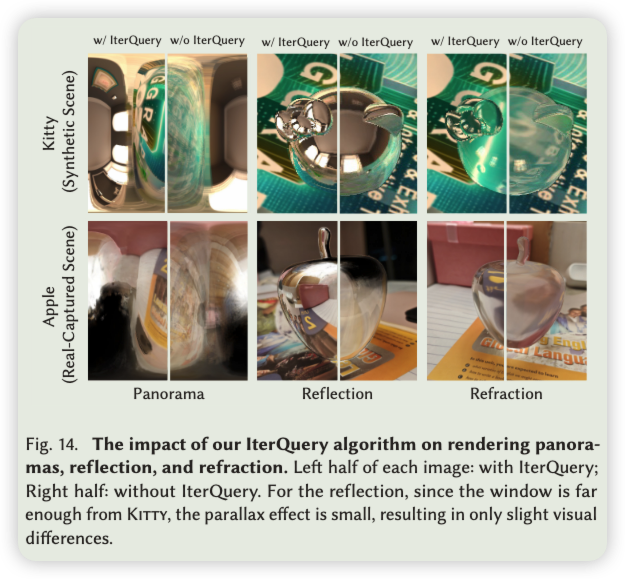
IterQuery算法的烧蚀研究。鉴于IterQuery算法在间接互反射和折射建模中起着至关重要的作用，我们进一步对算法进行了消融研究。我们使用图14中的高斯光场探针可视化渲染的全景图、反射图和折射图。可以观察到，在没有IterQuery的情况下，由于探针引入的视差，全景图和折射图都过于模糊。Kitty顶部窗口的反射光距离足够远，使得探针引入的视差可以忽略不计。然而，Kitty 底部的反射光由于其接近桌面而变得模糊。相反，我们的IterQuery算法有效地解决了视差问题，增强了渲染的细节。

不同的探针配置，如迭代次数、探针的数量和放置，也会影响迭代的收敛性和渲染结果，如图15所示。当K = 1时，收敛对探针的位置高度敏感。单个探针的有限感受野使得很难收敛到正确的解决方案。

应用

高效的高斯光场为许多高级应用打开了大门，包括第二射线效应，如镜子、折射以及使用非针孔相机的渲染，如图16所示。详情请参阅我们的补充视频。重建透明物体的重新渲染。我们将使用我们的透明GS重建的透明物体鼠标放入场景DrJohnson [Hedman et al.2018] 使用原始的 3D-GS [Kerbl et al. 2023] 重建以进行重新渲染。由于 TransparentGS 的重建质量和 GaussProbe 的查询质量，我们可以获得用于重新照明和材料编辑的逼真结果。此外，与其他基于 NeRF 的方法相比，我们的方法显示出显着的性能优势。插入网格的二次射线效应。我们使用传统的三角形网格（Ball、StanfordBunny、Happy、Mirror 和 Luck、彩色平面）、3D-GS [Kerbl et al. 2023]（DrJohnson、Playroom [Hedman et al. 2018]、Truck [Knapitsch et al. 2017]、Stump、Bicycle、Garden [Barron et al. 2022] 和 Lego [Mildenhall et al. 2020]）和透明高斯原语（Mouse、Apple、Penguin、Dog 和 Dolphin）来创建各种场景。GaussProbe在这些多目标组合场景中启用二次射线效应，如图1和图16所示，这对其他方法具有挑战性。

使用非针孔相机模型进行渲染 通过这种方式，我们还可以利用 GaussProbe 对非针孔相机进行渲染，例如 Playroom [Hedman et al.2018]与鱼眼相机和全景图

讨论和限制

我们的方法对分割结果的鲁棒性。由于我们使用语义分割来划分场景，我们验证了分割结果对透明物体重建的影响，如图17所示。可以观察到，虽然分割结果大多是准确的，但仍有不精确的区域，如海豚的嘴和老鼠的尾巴。然后，我们的方法通过对多个视图的监督，证明了对这种不准确性有足够的鲁棒性。

流形约束。对于我们的高斯光场探针，具有深度全景图的单个探针可以表示嵌入在 3D 空间中的二维流形。IterQuery 算法可以看作是沿流形滑动的移动点的过程，直到它与查询光线重合。

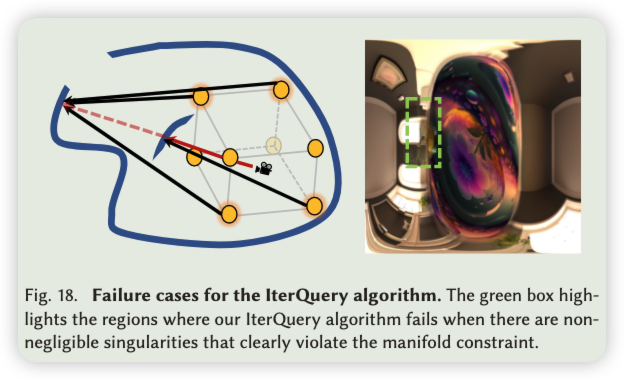
然而，如图18所示，在某些情况下会出现明显的不连续，违反了流形约束。在这种情况下，并非所有探针都收敛到要查询的光线和 3D 场景之间的第一个交点，从而导致不正确的结果。这也为失败案例 K = 1 提供了解释，如图 15 所示。幸运的是，这可以通过增加探针的数量并使用更优化的放置策略来解决。复杂的光路和歧义。光路对于模拟光在透明物体中的行为至关重要。与之前的方法类似 [Gao et al. 2023; Li et al.2023, 2020]，我们限制光反弹的数量。具体来说，我们假设光路恰好由两个折射组成，最多有一个总的内部反射，如图8中的HalfBall。然而，具有更多反弹的复杂光路可能会引入模糊性和奇点，这对反向渲染提出了挑战。因此，当使用消费级相机时，准确重建复杂的几何图形，如空心透明物体和复杂的自遮挡几何图形仍然具有挑战性。

此外，尽管我们的方法支持不同的 IOR（图 19），但高度异构的透明对象可能会在材料估计中引入歧义。这可以通过生成模型来解决，我们将其留作未来的工作。

不可见环境 与现有的基于 NeRF [Mildenhall et al. 2020] 或 3D-GS [Kerbl et al.] 的反向渲染方法类似。2023]（例如，Eikonal [Bemana et al.2022]或GShader [Jiang et al. 2024])，不完整的环境会影响不可见部分的重建。因此，为了提高重建的准确性，更好地捕获整个环境。

高斯射线追踪 由于以下原因，我们没有在我们的管道中选择 3D 高斯射线追踪 (3DGRT) [Moenne-Loccoz et al. 2024]。首先，3DGRT 目前不支持反向渲染和材料分解，正如其局限性所声称的那样。其次，与 3DGRT 不同，我们的 GaussProbe 不需要构建 BVH 或维护一个排序缓冲区，这使得它对我们的任务更有效。此外，GaussProbe 可以直接从使用原始 3DGS 训练的场景中获得，而 3DGRT 需要微调。也就是说，扩展 3DGRT 以重建透明物体将是一个有趣的未来工作。

因果渲染 由于我们的任务是反向渲染，我们更多地关注周围对对象外观的影响，而不是对象对其周围的影响(例如，焦散)。目前，基于3DGS的方法无法处理焦散渲染。这将是一个有趣的未来工作。

视频 我们在补充材料中提供了视频。视频中的一些视觉伪影主要来自采样、行进立方体算法的准确性和移动对象边界框引起的混叠。这些问题可以通过增加每个像素的样本来减轻，并增加探针的覆盖范围以完全包含动态对象移动范围内的区域等

结论

总之，我们提出了 TransparentGS，这是一个创新高效的基于3DGS的透明物体逆向渲染框架。通过引入透明高斯基元，将材料属性与位置和形状结合在一起，我们的方法能够基于物理的透明材料的渲染。为了保留折射细节，我们利用延迟折射策略来有效地捕捉镜面反射折射。针对光线追踪的高计算成本和光栅化在处理非相干二次光线时的局限性所带来的挑战，我们使用高斯光场探针(GaussProbe)来表示附近和遥远的光线变化，并伴随着IterQuery算法，该算法减轻了探针查询中的视差伪影。基于GaussProbe的管道允许我们在一个小时内重建任何透明对象，并促进逼真的渲染。它为多目标跟踪合成场景相互作用的复杂二次射线效应打开了大门。实验结果证实了我们框架的有效性和效率，突出了它推进透明物体的潜力。

虚拟游戏攻略