动态规划(Dynamic Programming)初步
本来是写哈希呢,让我想了半天这用哈希咋写。实在没想出来看了题解结果是动态规划······既然来都来了那就把题搞懂吧,又写了几道类似的题总结一下简单背包问题。
看了几道题下来还是非常的吃力的,但是觉得其实还是有规律可循的,经过题解大佬的点拨决定总结一下。动态规划的题目非常不固定,及其考验思维。但是希望通过这些“小规律”能让像我一样的小蒟蒻敲开DP的大门,对动态规划的思维有一定认识。
背包思路总结
基本规律:
01 背包问题:
最基本的背包问题就是 01 背包问题:一共有 N 件物品,第 i(i 从 1 开始)件物品的重量为 w[i],价值为 v[i]。在总重量不超过背包承载上限 W 的情况下,能够装入背包的最大价值是多少?
完全背包问题:
完全背包与 01 背包不同就是每种物品可以有无限多个:一共有 N 种物品,每种物品有无限多个,第 i(i 从 1 开始)种物品的重量为 w[i],价值为 v[i]。在总重量不超过背包承载上限 W 的情况下,能够装入背包的最大价值是多少?
可见 01 背包问题与完全背包问题主要区别就是物品是否可以重复选取。
背包问题具备的特征:
是否可以根据一个 target(直接给出或间接求出),target 可以是数字也可以是字符串,再给定一个数组 a,问:能否使用 a 中的元素做各种排列组合得到 target。
背包问题基本解法
01 背包问题:
如果是 01 背包,即数组中的元素不可重复使用,外循环遍历 a,内循环遍历 target,且内循环倒序:
完全背包问题:
(1)如果是完全背包,即数组中的元素可重复使用并且不考虑元素之间顺序,a 放在外循环(保证 a 按顺序),target在内循环且内循环正序。
(2)如果组合问题需考虑元素之间的顺序,需将 target 放在外循环,将 a 放在内循环,且内循环正序。
例题分析
力扣279完全平方数
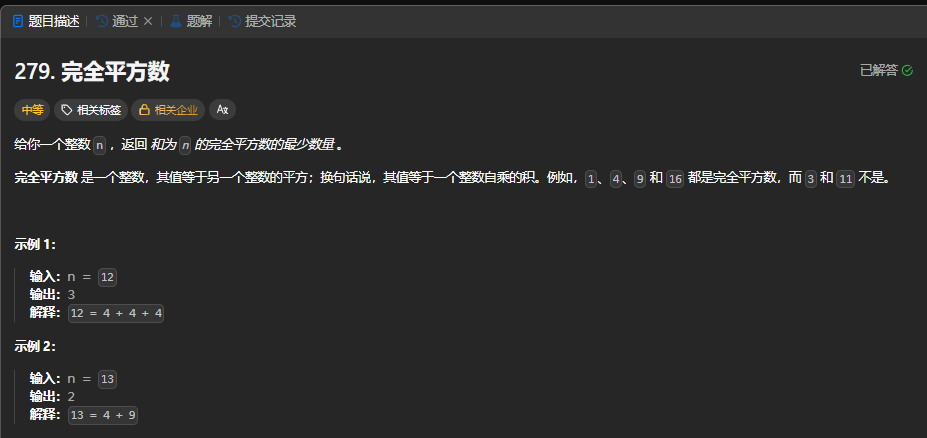
数组a:n之内的平方数(1,4,9,···,sqrt(n)要用这里的元素去凑n)
target:所给出的数字n(目标就是要凑n)
简单分析:
由于数组中的元素可以重复使用,比如样例1:4可以一直加,主要是求最少的数量,所以本问题是完全背包问题。元素之间的顺序不需要考虑:如果n=10的话,1+3+3和3+1+3是一样的。符合情况1:target放在内循环,a数组放在外循环且都是正序。
Code:
class Solution {public: int numSquares(int n) { vector dp(n+1, INT_MAX); dp[0]=0; for(int i=1; i<=sqrt(n); i++)//i*i为可能包含的平方数 { for(int j=0; j=i*i) dp[j]=max(dp[j], dp[j-i*i]+1); } } return dp[n]; }};力扣139单词拆分
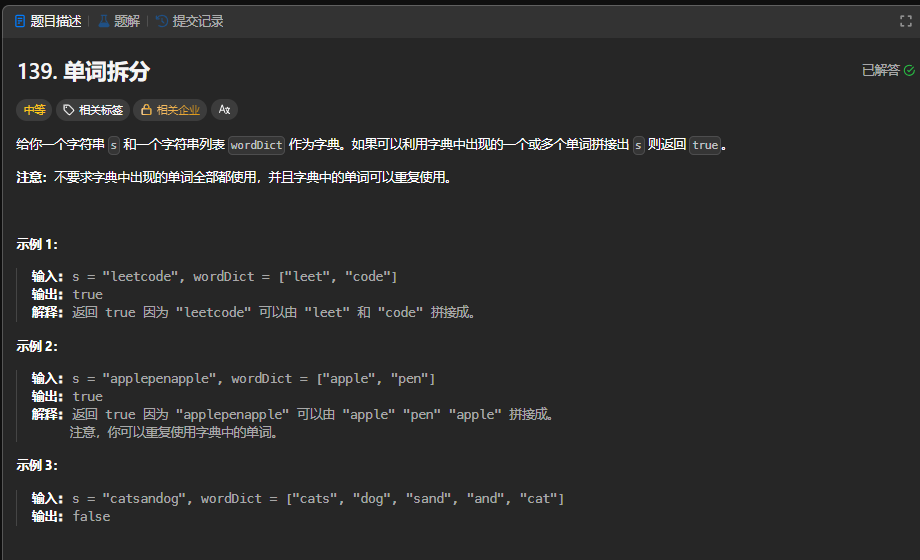
**数组a:**单词数组
**target:**目标字符串
简单分析:
由于数组中的单词可以重复使用,所以是完全背包问题。又由于数组中元素必须有序,比如只能是leetcode不能是codeleet,符合情况(2)。所以数组a放在外循环,按照应有的顺序。而单词数组放在内循环且为正序。
Code:
class Solution {public: int numSquares(int n) { vector dp(n+1, INT_MAX); dp[0]=0; for(int i=1; i<=sqrt(n); i++)//i*i为可能包含的平方数 { for(int j=1; j=i*i) dp[j]=min(dp[j], dp[j-i*i]+1); } } return dp[n]; }};力扣494目标和
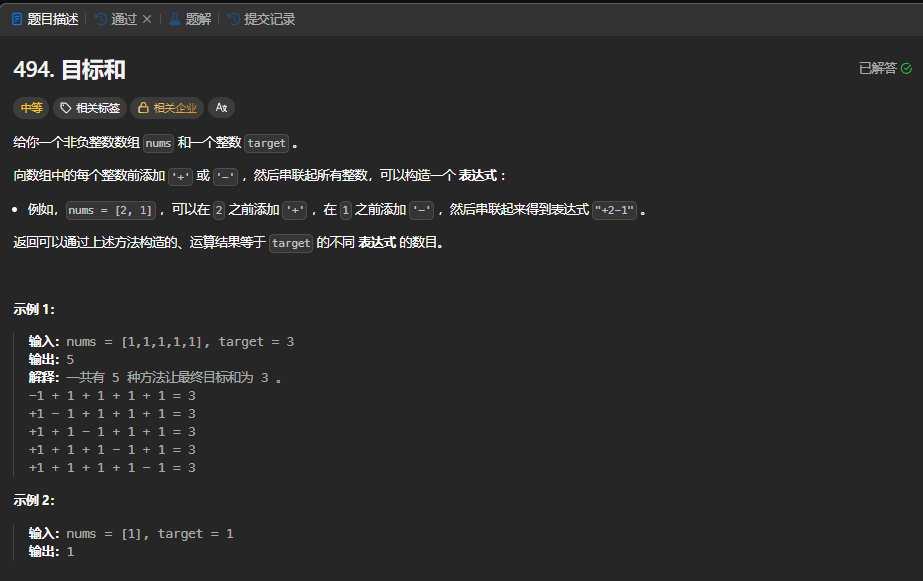
本题并不是直接给出target,需要进行一定的处理。首先筛选一下条件: if(target>sum||(target+sum)%2==1) return 0;
这是数学上的问题,可以推理一下。此时设x为所选的正数的和,y为所选的负数的绝对值和。则sum=x+y,target=x-y。由此可得:x=(sum+target)/2。这样就变成了一般的背包问题:到底选哪几个数能凑成x。此时再进行分析就明了的多了。
数组a: 所给数组nums
target: x
简单分析:
里面的元素不能重复选,只是普通的背包问题。所以外循环遍历a,内循环遍历target且为倒序。
Code:
class Solution {public: int findTargetSumWays(vector& v, int target) { int sum=0; for(auto i:v) sum+=i; target=fabs(target);//其实正负都是一样的 if(target>sum||(target+sum)%2==1) return 0;//简单数学知识 int t=(sum+target)/2;//选哪些数可以刚好等于正数x vector dp(t+1); dp[0]=1; for(auto n:v) { for(int i=t; i>=n; i--) dp[i] = dp[i] + dp[i-n]; } return dp[t]; }};力扣416分割等和子集
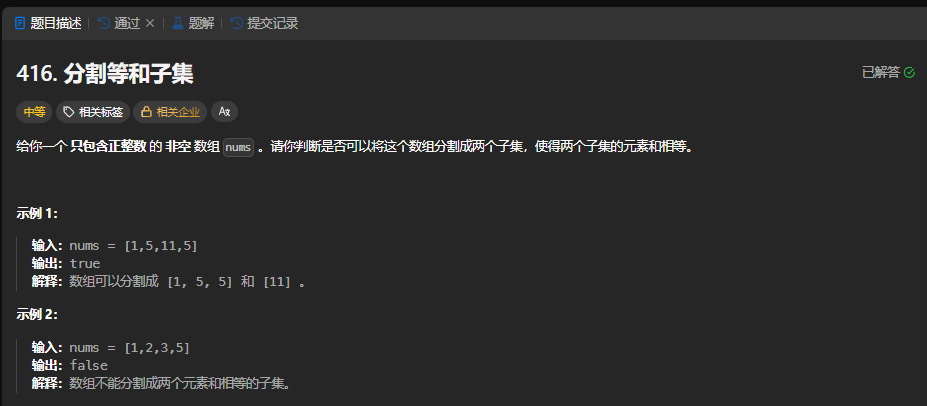
**数组a:**所给数组nums
target: sum/2
简单分析:
元素不能重复选择,所以只是普通背包问题。数组a在外层循环,内循环遍历target且为倒序
class Solution {public: bool canPartition(vector& v) { int sum=0; for(auto i:v) sum+=i; vector dp(sum+1); if(sum&1) return 0; dp[0]=true; int target=sum/2;//由于要分成两个集合目标值减半 for(auto i:v) { for(int j=target; j>=i; j--) dp[j]=dp[j]||dp[j-i]; } return dp[target]; }};力扣322零钱兑换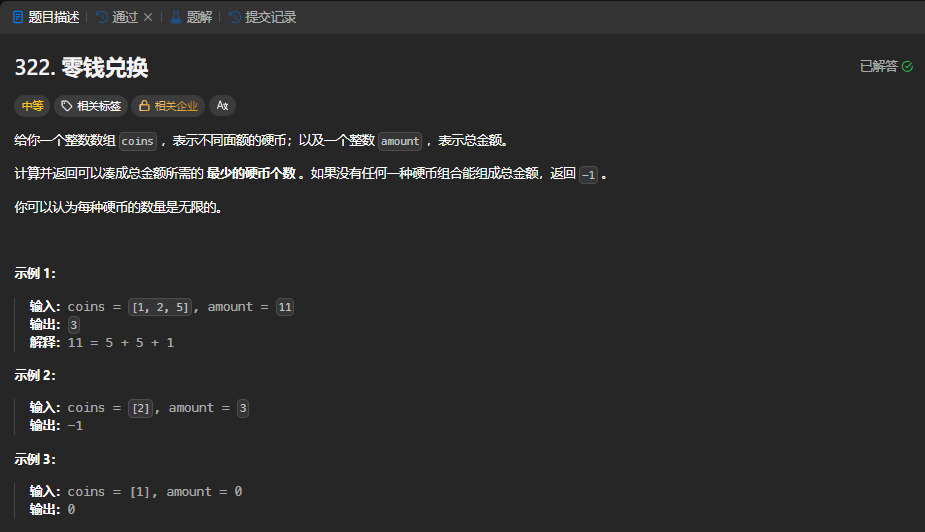
经过刚刚一系列的操作成功让主包浪费了一天的时间。但是对简单的背包问题也有了更好的认知。通过总结的规律做出这道基础题,也算今天的努力没有白费。废话不多说,按照前面几道题的方式,将本题进行解析。
**数组a:**coins
**target:**amount
简单分析:
由样例可以得知元素是可以重复的,所以属于完全背包问题。还有就是元素的顺序也没什么要求,所以本题符合完全背包的第2种情况:数组a在外层循环,target在内层且正序循环。
Code:
//数组a:coins//target:amount//可以重复,顺序无关,符合完全背包第1种//规律:a在外层,target在内层且正序class Solution {public: int coinChange(vector& co, int sum) { vector dp(100005,INT_MAX); dp[0]=0; for(auto i:co) { for(int j=1; j=i&&dp[j-i]!=INT_MAX) dp[j]=min(dp[j], dp[j-i]+1); } } if(dp[sum]==INT_MAX) return -1; return dp[sum]; }};这是第一次用MD编辑器,感觉排版非常的丑 !>_< 动态规划真的有点难搞啊,今天就先简单看看吧,之后肯定还会写关于动态规划的文章。


