数学建模案例精析与实战演练

本文还有配套的精品资源，点击获取

简介：《数学建模案题精编》是专为数学建模竞赛选手设计的实践参考资料，包含多种经典数学建模案例。本书通过案例分析，帮助学生提升数学建模技能，包含从问题定义到模型验证的全过程。书中案例涉及环境、经济、工程和生物等多个领域，指导学生如何将理论应用于实际问题，并通过具体案例提升解决实际问题的能力。

1. 数学建模基本概念与案例分析

1.1 数学建模简介

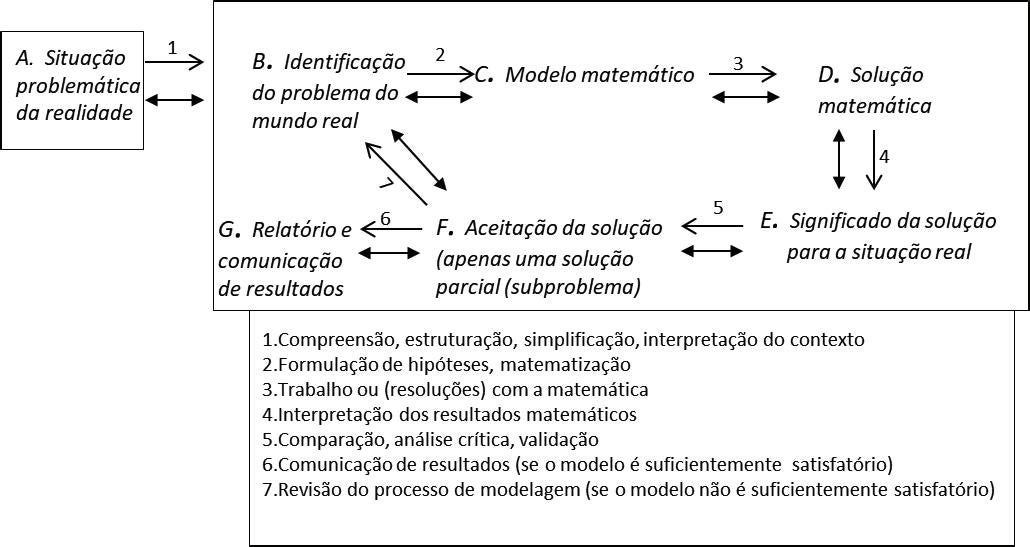
数学建模是将实际问题抽象化，并用数学语言表述的过程。在IT与相关领域中，数学模型可以用于模拟复杂系统的行为、优化资源分配，以及预测未来的发展趋势。建模过程通常包括假设条件的建立、模型的构建、求解以及验证和修正。

1.2 数学建模的案例分析

案例分析是理解数学建模的实际应用与效果的关键途径。本章将深入剖析数学建模在不同行业中的具体应用案例，如网络优化、市场分析、交通流量预测等。通过案例研究，读者将能了解建模过程中的关键环节和解决实际问题的策略。

2. 案例来源及其在不同领域的应用

2.1 数学建模案例的来源分析

在现代科学和工程问题中，数学建模已成为不可或缺的一环。它将现实世界的问题转化为数学问题，利用数学工具进行求解和分析。为了更好地理解和应用数学建模，对案例来源的分析至关重要。正确地搜集和筛选案例，以及评估数据来源的可靠性，对于建模过程的成功有着直接的影响。

2.1.1 案例的搜集与筛选方法

搜集数学建模案例的方法多种多样，可以从学术论文、行业报告、实际项目经验以及历史数据中获取。利用网络搜索引擎、专业数据库、同行推荐等手段，可以保证案例的多样性和全面性。筛选案例时，应该着重考虑以下几个因素：

• 相关性 ：案例需要与研究的目标问题密切相关。
• 复杂度 ：案例的复杂程度要适合研究者的技术水平和时间限制。
• 新颖性 ：优先选择最新的案例，以确保模型与当前实际情况相符。
• 多样性 ：多个领域的案例可以增加模型的普适性和创新性。

2.1.2 案例数据的来源与可靠性评估

案例数据的准确性和完整性直接影响模型的构建和验证。数据来源的多样性和权威性是评估数据可靠性的重要指标。常用的数据来源包括：

• 公共数据库 ：如政府统计部门、研究机构公开的数据集。
• 专业数据库 ：由商业公司维护的专业数据库，如彭博、路透等。
• 原始数据 ：直接从实地或实验中收集的数据。

评估数据可靠性时，可以使用以下方法：

• 来源审查 ：检查数据提供者的资质和数据收集的方法。
• 一致性检验 ：对比分析不同来源的数据，检查其一致性。
• 时间序列分析 ：评估数据随时间变化的趋势是否合理。
• 专家意见 ：借助领域专家的知识和经验进行评估。

2.2 案例在各领域的应用研究

数学建模案例在不同领域的应用展示其广泛的适用性和强大潜力。从工程技术到经济管理，再到生物医学，数学建模都发挥着其独特的作用。

2.2.1 工程技术领域的应用实例

在工程技术领域，数学建模可以应用于产品设计、流程优化、可靠性分析等多个方面。以汽车行业的碰撞安全模型为例，数学模型可以模拟不同速度和角度下车辆碰撞的效果，从而指导设计更安全的车辆结构。

2.2.2 经济管理领域的应用实例

经济管理领域中，数学建模帮助决策者理解和预测市场动态、评估投资风险、优化资源分配。例如，股票市场的预测模型可以根据历史数据和数学算法预测股票价格的走势，辅助投资者做出更明智的决策。

2.2.3 生物医学领域的应用实例

在生物医学领域，数学建模通过模拟人体生理过程或疾病传播过程来辅助医学研究和临床决策。例如，流行病学模型可以帮助理解传染病的传播机制，预测疫情的发展趋势，为公共卫生政策的制定提供依据。

通过上述案例的分析，我们不难发现数学建模不仅是一个理论工具，更是一个实践性强、应用范围广的方法。在不同领域的应用过程中，它帮助我们揭示了复杂现象背后的数学规律，为解决实际问题提供了有力支持。

3. 问题定义与目标设定

3.1 理解与分析问题

3.1.1 问题的分解与系统化理解

在数学建模的过程中，理解问题的本质是至关重要的一步。面对一个复杂的问题，首先需要将其进行分解，识别出各个子问题，并明确各个子问题之间的关系。通过系统化的理解，可以清晰地描绘出问题的结构，从而更好地解决问题。

系统的分解通常采用自顶向下的方法，从总问题出发，不断地细化各个分支，直至每个分支可以单独解决。例如，在交通流量模型的构建中，可以将整个交通系统分解为道路网络、车辆、驾驶员行为等多个子系统，并进一步细化到每个路口的信号控制、车辆排队理论等更小的单元。

子问题的确定需要遵循MECE原则（Mutually Exclusive, Collectively Exhaustive），即子问题之间要相互独立，同时所有子问题的集合要全面覆盖整个问题。这对于确保分析的完整性和避免遗漏关键因素至关重要。

3.1.2 需求分析与关键问题提炼

理解问题之后，接下来需要进行详细的需求分析。在这个阶段，我们要识别出不同利益相关者的需求，并将这些需求转化为具体的技术要求。例如，在构建一个城市交通模型时，可能需要考虑政府、市民、物流公司等不同群体的需求。

在需求分析的基础上，关键问题的提炼是至关重要的。这需要我们识别出哪些问题是模型需要解决的核心问题。关键问题的提炼往往涉及到专业知识、经验判断和直觉。借助于头脑风暴、德尔菲法等技术，可以有效地帮助团队聚焦问题的核心。

3.2 目标设定的策略与方法

3.2.1 明确模型的目标与功能

一旦关键问题被确定，下一步就是明确模型的目标和功能。模型的目标要具有明确性、可衡量性、可达成性、相关性和时限性（SMART原则）。这些目标将指导后续模型构建的方向和重点。

例如，在一个旨在减少交通拥堵的城市交通模型中，可能的目标包括：提高主要道路的通行能力、缩短高峰时段的车辆等待时间、提升公共交通的使用率等。这些目标需要具体、明确，并能够被量化。

模型的功能需要与目标紧密相连，确保模型能够在实际操作中提供有价值的输出。例如，模型可能需要提供不同交通方案的流量预测、拥堵分析、优化建议等。

3.2.2 设定可量化的目标标准

在确定了模型的目标后，接下来需要设定可量化的目标标准，以便于在模型求解和验证阶段进行评估。目标标准通常涉及性能指标、成本限制、时间约束等方面。

例如，在企业资源规划（ERP）系统优化模型中，目标标准可以是减少订单处理时间10%，降低库存成本5%等。这些量化的目标标准不仅为模型提供了评价标准，也为决策提供了依据。

目标标准的设定应当基于实际数据和前期的市场调研，保证其既有挑战性也具有实现的可能性。此外，目标标准的设定应保持一定的灵活性，以便在模型的迭代过程中进行调整。

在本章节中，我们介绍了问题定义与目标设定的重要性，说明了如何系统化地分解问题以及如何通过需求分析提炼关键问题。同时，我们也探讨了如何明确模型的目标与功能，并设定可量化的目标标准。这些步骤为后续模型的构建和验证提供了坚实的基础。

4. 模型构建与数学工具选择

4.1 模型构建的基本原理

4.1.1 模型的类型与选择依据

在构建模型时，选择合适的模型类型是至关重要的。模型的类型多种多样，包括但不限于线性模型、非线性模型、确定性模型、随机模型等。不同类型模型适用于解决特定的问题，例如，当问题的不确定性因素较多时，可能更倾向于选择随机模型。

选择模型类型时需要考虑以下几个因素：

1. 问题特性 ：需要解决的问题的复杂度和本质是选择模型类型的首要依据。比如，工程问题常常可以通过确定性模型来描述，而市场预测问题可能更适合使用随机模型。
2. 数据的可用性 ：数据的数量和质量也会影响模型选择。如果数据量充足且质量高，则可以考虑更复杂的模型以提高准确性。
3. 计算资源 ：模型的复杂程度决定了计算资源的需求。必须考虑是否具备足够的计算资源来处理选定的模型。
4. 实施成本 ：在商业应用中，需要考虑到模型构建和实施的成本，以确保项目的经济可行性。

4.1.2 模型的简化与假设条件

为了提高模型的可操作性和解题效率，通常需要对实际问题进行简化。简化的方法包括：

1. 忽略不重要的因素 ：在不影响结果的前提下，忽略一些影响较小的因素。
2. 引入假设条件 ：为了使问题变得易于处理，需要设定一些合理的假设条件。
3. 采用近似方法 ：在保证精确度的前提下，对某些难以精确计算的部分采用近似处理。

模型的简化和假设是将复杂现实问题转化为可解数学问题的关键步骤，然而也应注意，过度简化或不合理的假设可能会导致模型预测失效。因此，在进行模型简化时，需要不断与实际问题对照验证模型的适用性。

4.2 数学工具的应用与选择

4.2.1 常用数学工具介绍

在数学建模过程中，各种数学工具发挥着重要的作用，常用的数学工具有：

• 线性代数 ：用于解决多变量问题和系统方程。
• 微积分 ：在处理变化率和累积量的问题时不可或缺。
• 概率论与数理统计 ：为不确定性和随机性问题提供解决方案。
• 优化理论 ：寻找问题的最优解或近似最优解。
• 运筹学 ：涉及优化和决策理论，在资源分配问题中十分有用。

选择合适的数学工具，对于解决特定问题至关重要。应根据问题的特点选择合适的数学工具，例如，涉及流量计算的交通问题，可能更适用图论中的算法进行处理。

4.2.2 工具选择的决策过程

选择合适的数学工具是一个迭代和反馈的过程。这一过程通常包括以下步骤：

1. 问题分析 ：首先对问题进行深入分析，理解其本质和需求。
2. 初步选择 ：根据问题的特性初步选择一组可能适用的工具。
3. 可行性分析 ：对初步选定的工具进行可行性分析，评估其在问题中的适应性和有效性。
4. 实验验证 ：通过实验和实际计算来测试工具在模型中的表现。
5. 结果评估与调整 ：分析实验结果，评估模型的准确性和可靠性。如果效果不理想，需要返回到前面的步骤重新进行选择。

例如，在进行供应链优化时，可能首先考虑使用线性规划和网络流优化理论，但随着模型细节的增加，可能会发现需要结合整数规划或启发式算法以获取更好的解决方案。

选择合适的数学工具是数学建模成功的关键，它不仅需要深厚的专业知识，还需要丰富的经验和对问题深刻的理解。

5. 数据处理与分析方法

在本章节中，我们将深入了解数据处理与分析方法的重要性，这是数学建模中的一个关键环节。数据处理是确保模型质量的基础，而数据分析方法的选择和应用则是实现模型目标的关键手段。本章将从数据预处理的策略与技巧开始，逐步深入到数据分析方法的运用，并辅以实例和详细解读。

5.1 数据预处理的策略与技巧

数据预处理是任何数据分析项目的基础，它是改善数据质量、提高分析准确性的重要步骤。预处理过程包括但不限于数据清洗、数据质量控制、数据变换和规范化处理。

5.1.1 数据清洗与质量控制

数据清洗的目的是识别并解决数据中的错误、不一致或不完整的问题。数据质量控制涉及检测数据集中的异常值、缺失值和噪声。

在实际操作中，数据清洗通常遵循以下步骤：

1. 数据识别 ：识别数据集中的重复记录、缺失值和错误。
2. 数据清洗 ：处理重复记录，填充或删除缺失值，修正错误。
3. 数据验证 ：确保数据清洗后的结果符合预期，例如统计一致性。

一个简单的数据清洗代码示例，使用Python进行操作：

import pandas as pd# 读取数据data = pd.read_csv(\'data.csv\')# 数据清洗：删除缺失值data_cleaned = data.dropna()# 数据清洗：填充缺失值data_filled = data.fillna(method=\'ffill\')# 数据清洗：移除重复记录data_unique = data.drop_duplicates()# 保存清洗后的数据data_cleaned.to_csv(\'data_cleaned.csv\', index=False)

在此代码块中， dropna() 函数删除了缺失值， fillna() 函数用之前的数据填充了缺失值，而 drop_duplicates() 函数移除了重复的记录。通过这些步骤，数据质量得到了显著提高。

5.1.2 数据变换与规范化处理

数据变换是将数据转换为适合分析的格式，而规范化处理则是将数据缩放到一个标准的范围或分布，以消除不同数据尺度和量纲带来的影响。

常见的数据变换方法包括：

• 标准化 ：将数据按比例缩放，使之落入一个小的特定区间，如[0, 1]。
• 归一化 ：数据减去均值后除以标准差，使得数据均值为0，标准差为1。
• 对数转换 ：减少数据的偏斜度，对于具有指数分布的数据非常有用。

一个标准化数据的例子代码如下：

from sklearn.preprocessing import StandardScaler# 创建一个标准化器scaler = StandardScaler()# 使用标准化器处理数据data_normalized = scaler.fit_transform(data)# 将标准化后的数据转换为DataFramedata_normalized_df = pd.DataFrame(data_normalized, columns=data.columns)

在本小节中，我们讨论了数据预处理的策略与技巧，包括数据清洗与质量控制以及数据变换与规范化处理，同时提供了相应的代码示例及其逻辑分析。预处理后的高质量数据为后续的分析工作打下了坚实的基础。

6. 模型求解策略与技术

在数学建模过程中，模型求解是实现模型功能，达到预期目标的关键步骤。求解策略不仅取决于模型的类型，还需要考虑可用技术以及计算资源等因素。本章节将介绍模型求解的基本方法，并深入探讨如何利用先进技术和环境来提升求解效率和模型准确性。

6.1 模型求解的基本方法

6.1.1 数值计算方法概述

数值计算方法是求解数学模型中最为常用的一类方法，它们通过近似计算来处理模型中的非线性、高维或复杂计算问题。这一小节将对以下几种常见的数值计算方法进行介绍：

• 迭代法 ：迭代法是一种逐步逼近数值解的方法，适用于线性或非线性方程求解。常见的迭代法包括雅可比法、高斯-赛德尔法等。
• 线性规划与非线性规划 ：线性规划是在一组线性约束条件下对线性目标函数进行最大化或最小化的过程。非线性规划则是在非线性约束条件下对非线性目标函数进行优化。
• 蒙特卡罗模拟 ：蒙特卡罗方法基于随机抽样原理，适用于求解复杂的概率和统计问题，如随机过程、风险评估等。

% 示例代码：使用MATLAB中的fsolve函数进行非线性方程求解function x = solve_nonlinear(f, x0) % f为非线性方程 % x0为初始猜测值 options = optimoptions(\'fsolve\',\'Display\',\'iter\'); [x, fval, exitflag, output] = fsolve(f, x0, options);end

在上述MATLAB代码中， fsolve 函数被用来求解非线性方程。代码执行的逻辑是定义一个求解函数 solve_nonlinear ，该函数接受非线性方程 f 和初始猜测值 x0 作为输入，并输出求解结果 x 、函数值 fval 、退出标志 exitflag 以及输出信息 output 。

6.1.2 模拟与优化方法

模拟方法通常用于模拟现实世界的问题，帮助我们理解和预测系统的行为。优化方法则专注于找到最优解，减少成本、时间或资源消耗。本小节将详细介绍以下内容：

• 确定性优化与随机优化 ：确定性优化方法，如线性规划，假设所有参数都是已知的。而随机优化考虑不确定性因素，通过概率分布来描述这些参数。
• 多目标优化 ：当存在多个优化目标时，如成本和效率的平衡，需要使用多目标优化方法。这涉及到帕累托前沿的确定和权衡分析。
• 启发式算法 ：启发式算法，如遗传算法、蚁群算法等，基于自然或生物系统的机制，适合解决复杂的优化问题。

# 示例代码：使用Python进行简单遗传算法实现import numpy as npdef fitness_function(x): # 这里定义适应度函数 return - (x[0] - 1)**2 - (x[1] - 2.5)**2def genetic_algorithm(pop_size, num_generations): population = np.random.rand(pop_size, 2) for generation in range(num_generations): # 计算适应度 fitness = np.array([fitness_function(ind) for ind in population]) # 选择下一代 parents = population[np.argsort(fitness)[-2:]] # 选择适应度最高的两个个体 # 交叉与变异（这里简化处理） offspring = np.vstack([parents, parents]) # 简单的交叉，实际中需要复杂的交叉逻辑 population = offspring return population[np.argmax(fitness)]# 调用遗传算法求解best_solution = genetic_algorithm(100, 100)

在上述Python示例中，我们使用了一个非常简化的遗传算法来解决优化问题。代码逻辑是首先定义一个适应度函数 fitness_function ，然后通过 genetic_algorithm 函数实现遗传算法。这个过程中包括选择、交叉、变异等遗传算法的基本步骤。

6.2 先进技术在模型求解中的应用

6.2.1 人工智能技术在模型中的应用

随着人工智能技术的快速发展，其在数学建模和模型求解中的应用变得日益广泛。以下为人工智能技术在模型求解中的几个应用实例：

• 机器学习模型 ：机器学习模型能够通过历史数据学习到数据间的复杂关系，并对未来数据进行预测。
• 深度学习 ：深度学习模型，特别是卷积神经网络(CNN)和循环神经网络(RNN)，在图像识别、自然语言处理等地方取得突破。
• 强化学习 ：强化学习能够模拟决策过程，通过试错来找到最优策略。

6.2.2 大数据与云计算环境下的模型求解

大数据环境下，模型求解面对的数据量和复杂性都有极大的增加。云计算提供了弹性的计算资源，使得模型求解更加高效和经济。以下为在大数据与云计算环境下模型求解的几个关键点：

• 分布式计算 ：分布式计算框架如Apache Hadoop和Apache Spark能够处理大规模数据集，并在多节点上并行计算。
• 容器化与服务化 ：利用Docker容器化技术和Kubernetes服务编排来部署模型求解任务，可以提高计算资源利用率，并简化部署过程。
• 边缘计算 ：将数据处理和模型求解任务部署到网络边缘（即数据产生地附近），减少数据传输延迟，并提高实时性。

graph TD A[数据源] -->|数据流| B(数据处理层) B -->|处理后的数据| C[分析与模型层] C -->|模型求解任务| D(云计算资源) D -->|计算结果| E[结果存储与分析]

在上面的mermaid流程图中，简述了一个典型的在云计算环境下进行模型求解的数据处理流程。从数据源开始，数据流到数据处理层，处理后的数据传输到分析与模型层进行求解，并最终将计算结果存储和分析。

通过本章节的介绍，我们了解了模型求解的基本方法和先进科技的应用，以及在实际求解过程中可能遇到的多种技术问题和解决方案。接下来的章节将探讨如何验证模型的有效性和准确性，并进行必要的改进，以达到最佳的建模效果。

7. 模型验证与改进方法

模型验证与改进是整个数学建模过程中至关重要的一步，它保证了模型的有效性以及对未来预测的准确性。一个经过验证和改进的模型能够更好地反映实际情况，并在实际应用中提供更精确的决策支持。本章节将对模型验证的策略、模型改进的途径进行深入探讨。

7.1 模型的验证策略

在模型构建完毕后，验证模型是确保其有效性和可靠性的必经之路。验证过程通常包括以下几个方面：

7.1.1 模型的敏感性分析

敏感性分析是一种用来评估模型输出对于输入参数变化的敏感程度的方法。通过此分析可以识别出影响模型结果的关键参数，并且可以对这些关键参数进行优先级排序，从而更有效地进行模型的校准。

graph LRA[开始] --> B[确定参数]B --> C[设定参数变动范围]C --> D[运行模型]D --> E[记录输出结果]E --> F[分析结果变化]F --> G[识别关键参数]G --> H[排序关键参数]

7.1.2 模型的交叉验证方法

交叉验证是一种统计学方法，用于评估并改善模型的泛化能力。它通常包括将数据集分为训练集和测试集，然后通过多次迭代，每次使用不同的训练集和测试集组合，来验证模型的稳健性。这种方法在机器学习领域尤为常用，它可以显著减少模型对于特定数据集的过拟合现象。

from sklearn.model_selection import cross_val_score# 假设 X 是特征数据，y 是目标变量，clf 是分类器模型scores = cross_val_score(clf, X, y, cv=5) # 进行5折交叉验证print(\"Accuracy: %0.2f (+/- %0.2f)\" % (scores.mean(), scores.std() * 2))

7.2 模型的改进与优化

模型验证后，接下来需要根据验证结果对模型进行调整，以提升模型的性能。

7.2.1 根据验证结果的模型调整

模型调整可以基于敏感性分析的结果进行。通过识别关键参数，我们可以对这些参数进行微调，或者引入新的数据来改善模型输出。在某些情况下，可能还需要回溯到模型构建阶段，重新选择模型类型或数学工具。

7.2.2 模型的动态优化与迭代更新

动态优化意味着模型在使用过程中会根据新收集的数据不断进行调整。这是一个迭代过程，模型需要不断地被测试、评估和调整。这一过程通常需要一个反馈机制，用以收集模型表现的数据，并且持续地对模型进行微调和优化。

# 模拟一个模型动态优化的过程def optimize_model(model, data, target, iterations=10): for i in range(iterations): model.fit(data, target) predictions = model.predict(data) # 假设我们有办法衡量预测的准确度 accuracy = evaluate_predictions(predictions, target) # 根据预测准确度调整模型参数 model = adjust_parameters(model, accuracy) return model# 在实际应用中，evaluate_predictions和adjust_parameters需要具体实现

模型验证与改进是确保数学模型能够适应未来变化和提供准确预测的核心步骤。通过不断的验证、调整、优化，我们可以构建出既稳定又灵活的模型，使其能够适应不断变化的数据和环境条件。

本文还有配套的精品资源，点击获取

简介：《数学建模案题精编》是专为数学建模竞赛选手设计的实践参考资料，包含多种经典数学建模案例。本书通过案例分析，帮助学生提升数学建模技能，包含从问题定义到模型验证的全过程。书中案例涉及环境、经济、工程和生物等多个领域，指导学生如何将理论应用于实际问题，并通过具体案例提升解决实际问题的能力。

本文还有配套的精品资源，点击获取