深入理解动态规划：斐波那契数列、最长公共子序列和背包问题的分析_重叠子问题

目录

零、动态规划的核心思想

一、斐波那契数列（Fibonacci Sequence）

二、最长公共子序列（Longest Common Subsequence, LCS）

三、背包问题（Knapsack Problem）

四、总结

动态规划（Dynamic Programming, DP）是一种强大的算法设计方法，广泛应用于解决那些能够分解为多个重叠子问题的复杂问题。通过将问题拆解为子问题并存储其解，避免了重复计算，从而显著提高了解决问题的效率。动态规划不仅可以帮助你解决算法问题，还能提升你对问题分解和优化的能力。

对于嵌入式软件工程师来说，掌握动态规划的思想不仅有助于解决算法问题，更能在资源有限的嵌入式系统中优化资源分配与任务调度等问题。嵌入式系统中虽然资源有限，但动态规划的思想可以应用于优化资源分配、任务调度等问题。

零、动态规划的核心思想

动态规划的核心是将复杂问题分解为子问题，并通过存储子问题的解（通常用数组或表格）来避免重复计算。动态规划问题通常具有以下两个特性：

重叠子问题：子问题会被多次重复计算。

最优子结构：问题的最优解可以通过子问题的最优解推导出来。

嵌入式系统中的许多问题（如任务调度、资源分配）也具备这些特性，因此动态规划的思想可以很好地应用。

一、斐波那契数列（Fibonacci Sequence）

问题描述：

斐波那契数列是一个数字序列，通常定义如下：

F(0) = 0

F(1) = 1

F(n) = F(n-1) + F(n-2) (n ≥ 2)

求解第n个斐波那契数。

方案一：使用两个变量的迭代方法

#include\"stdio.h\"//斐波那契数 int main(){int res,n,res1,res2,i;scanf(\"%d\",&n);if(n==0)res=0;else if(n==1)res=1;else {res1=1;res2=0;for(i=2;i<=n;i++){res=res1+res2;printf(\"FN[%d]=%d\\n\",i,res);res2=res1;res1=res;} }printf(\"res=%d\",res);}

方案二、动态规划解法：

动态规划思路：

1. 子问题：F(n) 可以通过 F(n-1) 和 F(n-2) 计算得到。

2. 重叠子问题：F(n-1) 和 F(n-2) 会被多次计算，因此我们需要存储这些计算结果。

3. 最优子结构：F(n) 是由其子问题 F(n-1) 和 F(n-2) 最优解得到的。

使用一个数组 dp[] 来存储每个斐波那契数，避免重复计算。

#include int fibonacci(int n) { if (n <= 1) return n; int dp[n+1]; // 创建一个长度为n+1的数组 dp[0] = 0; dp[1] = 1; // 填充 dp 数组 for (int i = 2; i <= n; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n];}int main() { int n = 10; printf(\"Fibonacci of %d is %d\\n\", n, fibonacci(n)); return 0;}

时间复杂度：O(n)，我们只需要循环 n 次，存储中间结果。

比较总结：

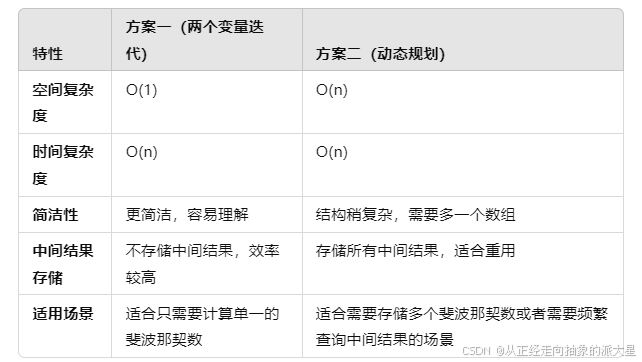
如果你只需要计算一个斐波那契数，并且不关心中间结果，方案一 是更优选择，因为它的空间复杂度为常数级别，且效率较高。

如果你需要计算多个斐波那契数，或者需要存储中间结果以便重复使用，方案二 更加适合，尽管它需要额外的空间来存储结果，但可以利用动态规划的思想来高效地计算并缓存所有中间结果。

二、最长公共子序列（Longest Common Subsequence, LCS）

问题描述：

给定两个字符串 X 和 Y，找出它们的最长公共子序列。子序列是指通过删除某些字符（可以不删除任何字符）使得剩下的字符按原顺序排列的字符串。

动态规划思路：

1. 子问题：对于 X[i] 和 Y[j]，有两种选择：

   如果 X[i] == Y[j]，则最长公共子序列是 LCS(i-1, j-1) + 1；
   否则，最长公共子序列为 max(LCS(i-1, j), LCS(i, j-1))

2. 重叠子问题：计算 LCS(i, j) 时，很多子问题会重复计算。

3. 最优子结构：LCS(i, j) 的值依赖于其子问题的值。

动态规划解法：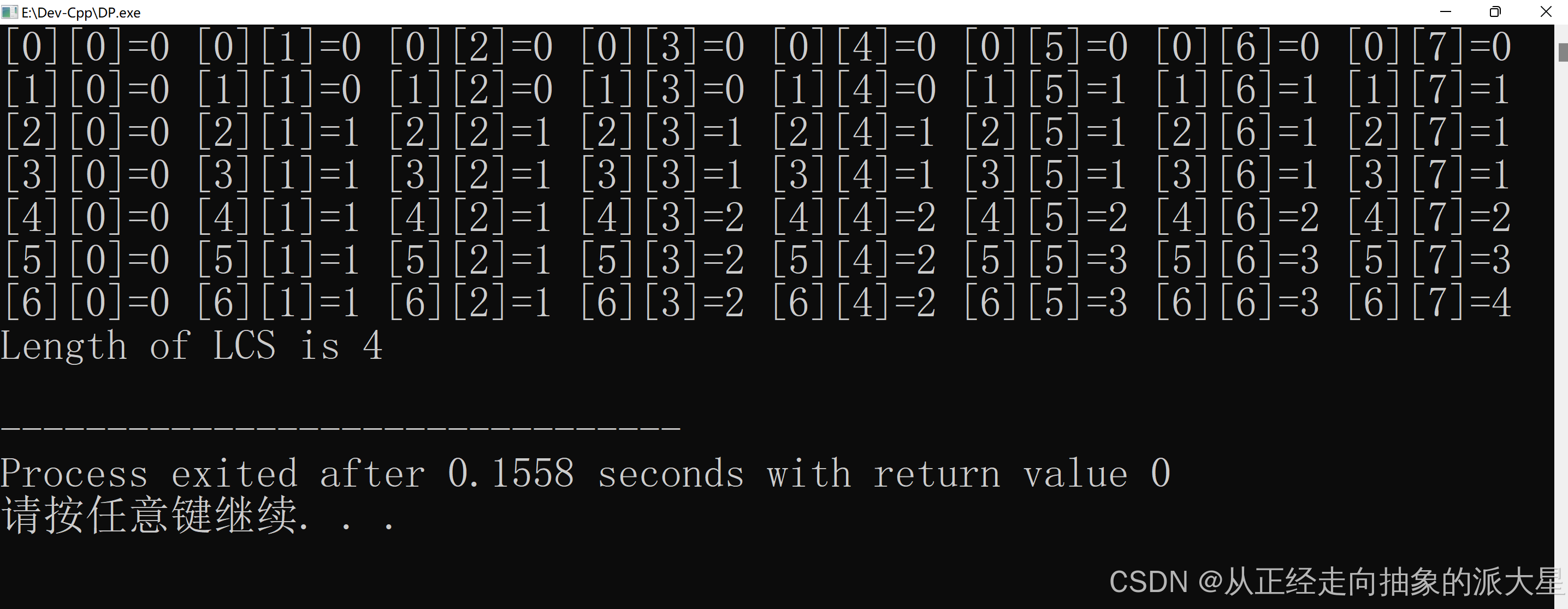

使用二维数组 dp[i][j] 来存储 X[0...i-1] 和 Y[0...j-1] 的最长公共子序列长度。

#include #include // LCS（Longest Common Subsequence，最长公共子序列）函数int lcs(char *X, char *Y) { int m = strlen(X); // 获取字符串 X 的长度 int n = strlen(Y); // 获取字符串 Y 的长度 // 创建二维动态规划数组 dp，dp[i][j] 表示 X[0...i-1] 和 Y[0...j-1] 的最长公共子序列长度 int dp[m+1][n+1]; // 初始化 DP 表 for (int i = 0; i <= m; i++) { for (int j = 0; j  dp[i][j-1]) ? dp[i-1][j] : dp[i][j-1]; } } // 返回 X 和 Y 的最长公共子序列的长度 return dp[m][n];}int main() { // 示例字符串 X 和 Y char X[] = \"AGGTAB\"; // 字符串 X char Y[] = \"GXTXAYB\"; // 字符串 Y // 调用 lcs 函数，计算并输出最长公共子序列的长度 printf(\"Length of LCS is %d\\n\", lcs(X, Y)); return 0;}

时间复杂度：O(m * n)，其中 m 和 n 分别是字符串 X 和 Y 的长度。

三、背包问题（Knapsack Problem）

问题描述：

给定一个背包，背包可以承受的最大重量为 W，有 n 个物品，每个物品有重量和价值。要求在不超过背包最大承载重量的情况下，选择一些物品使得它们的总价值最大。

动态规划思路：

1. 子问题：对于每个物品 i，我们有两种选择：

   不选择第 i 个物品，价值为 dp[i-1][w]
   选择第 i 个物品，价值为 dp[i-1][w - wt[i]] + val[i]

2. 重叠子问题：对于每个重量值 w，很多子问题会重复计算。

3. 最优子结构：dp[i][w] 的值依赖于它的子问题。

动态规划解法：

使用二维数组 dp[i][w] 来存储前 i 个物品在背包容量 w 下的最大价值。

#include // 背包问题的动态规划解法int knapsack(int W, int wt[], int val[], int n) { // 创建一个二维数组 dp，其中 dp[i][w] 表示前 i 个物品在背包容量为 w 时的最大价值 int dp[n+1][W+1]; // 初始化 DP 表 for (int i = 0; i <= n; i++) { for (int w = 0; w <= W; w++) { if (i == 0 || w == 0) dp[i][w] = 0; // 如果没有物品或者背包容量为 0，最大价值为 0 else if (wt[i-1]  dp[i-1][w - wt[i-1]] + val[i-1]) ? dp[i-1][w] : dp[i-1][w - wt[i-1]] + val[i-1]; else dp[i][w] = dp[i-1][w]; // 如果当前物品的重量大于背包容量，不能选择当前物品 } } // dp[n][W] 存储的是 n 个物品，背包容量为 W 时的最大价值 return dp[n][W];}int main() { // 定义物品的价值和重量数组 int val[] = {60, 100, 120}; // 每个物品的价值 int wt[] = {10, 20, 30}; // 每个物品的重量 int W = 50; // 背包的最大容量 int n = sizeof(val) / sizeof(val[0]); // 物品的数量 // 调用 knapsack 函数，计算并输出最大价值 printf(\"Maximum value in Knapsack = %d\\n\", knapsack(W, wt, val, n)); return 0;}

时间复杂度：O(n * W)，其中 n 是物品数量，W 是背包容量。

四、总结

动态规划是一种高效的算法设计策略，适用于许多具有重叠子问题和最优子结构的问题。通过将问题分解为子问题，并缓存中间结果，可以大大提高算法的效率。通过斐波那契数列、最长公共子序列和背包问题，我们可以看到动态规划如何在不同的场景中发挥作用。

学习动态规划的关键在于理解：将子问题解出并将其存储下来用于解接下来的问题

1. 如何定义子问题；

2. 如何将子问题的解存储起来；

3. 如何根据子问题的解来构建问题的最优解。