线段树学习笔记 - 练习题（3）

文章目录

• 1. 前言
• 2. 线段树维护区间合并问题
• 3. 洛谷 P2572 [SCOI2010] 序列操作
• 4. 洛谷 P6492 [COCI 2010/2011 #6] STEP
• 5. 洛谷 P1503 鬼子进村
• 6. P2894 [USACO08FEB] Hotel G

1. 前言

线段树系列文章：

• 线段树学习笔记。
• 线段树学习笔记 - 练习题（1）。
• 线段树学习笔记 - 练习题（2）。

前一篇做了几道线段树的题目，这篇文章就继续看下线段树的相关题目，还是一样，学习视频：算法讲解113【扩展】线段树专题4-线段树解决区间合并的问题，题目都是左神视频上的，思路也可以看这个视频。

2. 线段树维护区间合并问题

假设现在有一个题目，给定一个长度为 n 的数组 arr，内部只有 0 和 1 两种值，下标从 1 开始，现在需要维护 [l，r] 范围上面连续 1 的最长子串长度，那么这个要怎么维护。

首先最长连续 1 这个事，父亲节点能不能根据子节点来得到，假设我们现在可以通过 max 数组维护左右两个子节点的最长连续 1。答案是不可以，比如下面的情况。

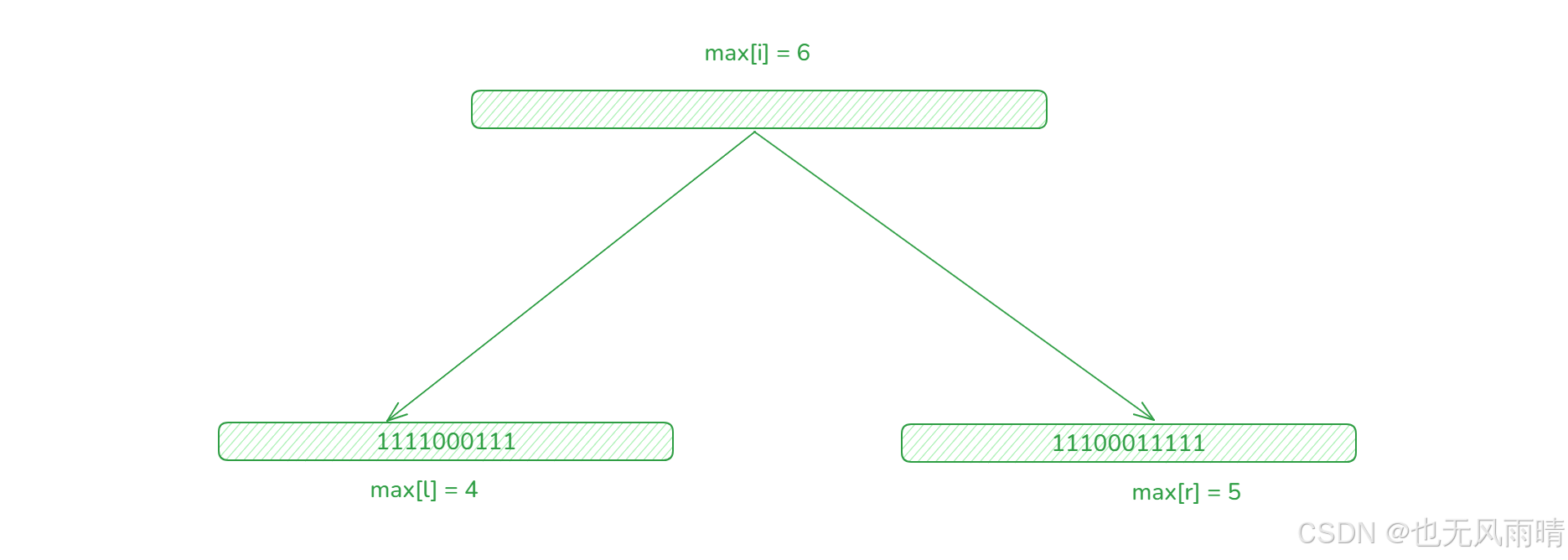
左子节点是 1111000111，最大连续 1 的子串长度是 4，右子节点是 11100011111，最大连续 1 的子串长度是 5，但是汇总之后父结点 max[i] = 6，就是左串和右串拼起来之后中间那一段 1 也拼起来了，所以可以看到只通过一个数组是不可以完成最长连续 1 的维护问题的。

既然用一个数组没办法解决这个事，我们就用三个数组去维护，len 数组维护连续 1 的最长子串长度，pre 维护连续 1 的最长前缀，suf 维护连续 1 的最长后缀，定义好之后下面的线段树就是这样的。

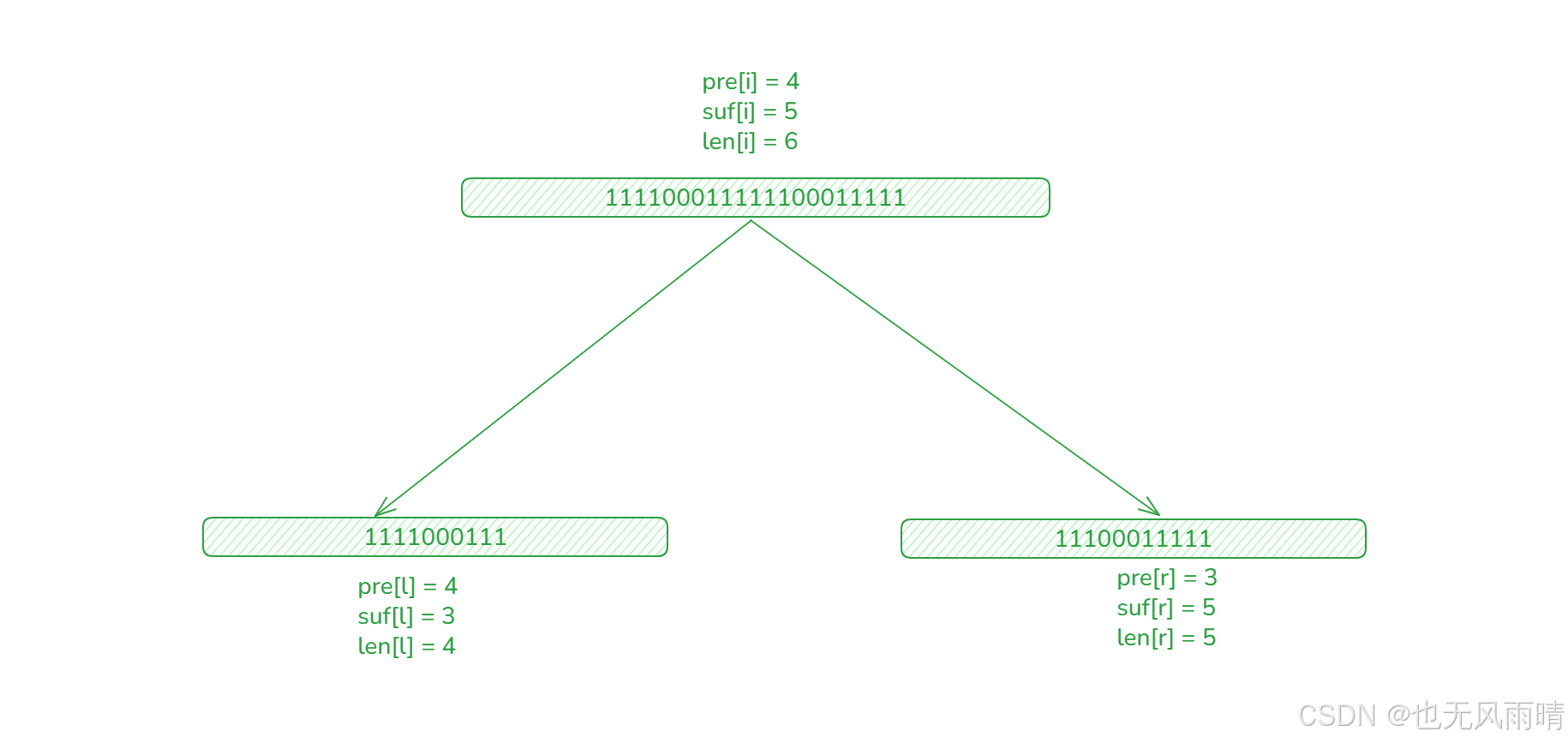
可以看到，对于左节点 pre[l] = 4，suf[l] = 3，len[l]= 4，对于右节点 pre[r] = 3，suf[r] = 5，len[r] = 5。那么父结点的这三个数组需要怎么维护呢？最直观看着就是：

• pre[i] = pre[l] = 5
• suf[i] = suf[r] = 5
• len[l] = Math.max(len[l]，Math.max(len[r]，suf[l] + pre[r])) = 6

这样直观看起来确实没什么问题，父结点的最长前缀就取左节点的 pre[l] 值，最长后缀就取右节点的 suf[r] 值，然后最长长度分别取左右节点的 len 以及左节点的 suf[l] 加上右节点的 pre[r] 作比较取最大值，实际上 len 这样取是没问题的，但是 pre 和 suf 还得再加工一下，比如遇到下面这种情况。

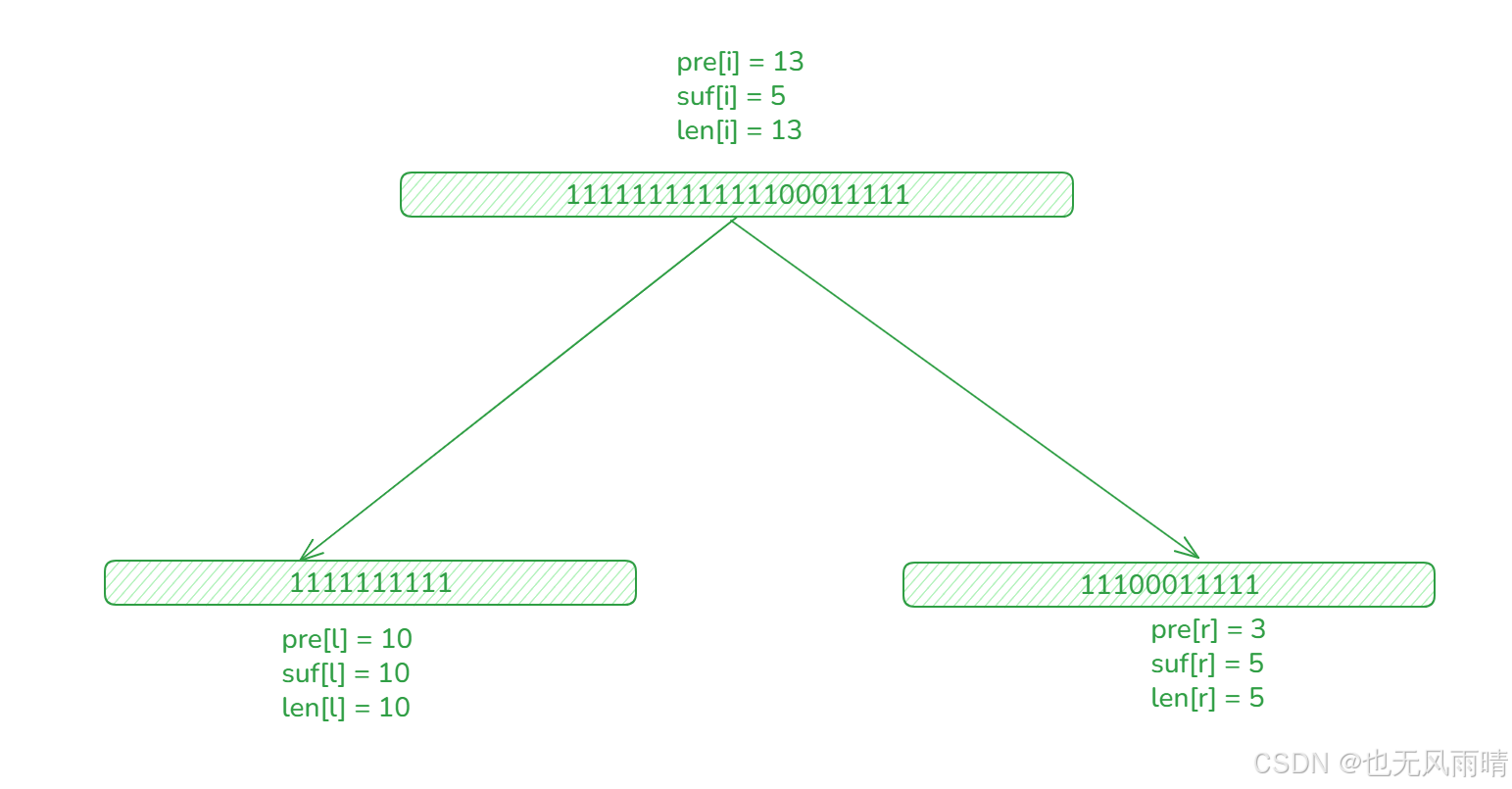
可以看到左节点全部都是 1，这种情况下 pre[l] = suf[l] = len[l] = 10，那么更新父结点的 pre 的时候就不能简单设置 pre[i] = pre[l]，还得加上 pre[r]，所以可以这么写：pre[i] = pre[l] < ln ? pre[l] : pre[l] + pre[r]，然后更新 suf[i] 可以写成：suf[i] = suf[r] < rn ? suf[r] : suf[l] + suf[r]，更新 len[i] 还是一样，不需要变，这样我们就更新好了这个线段树。

3. 洛谷 P2572 [SCOI2010] 序列操作

P2572 [SCOI2010] 序列操作

题目描述

lxhgww 最近收到了一个 $01$ 序列，序列里面包含了 $n$ 个数，下标从 $0$ 开始。这些数要么是 $0$，要么是 $1$，现在对于这个序列有五种变换操作和询问操作：

• 0 l r 把 $[l,r]$ 区间内的所有数全变成 $0$；
• 1 l r 把 $[l,r]$ 区间内的所有数全变成 $1$；
• 2 l r 把 $[l,r]$ 区间内的所有数全部取反，也就是说把所有的 $0$ 变成 $1$，把所有的 $1$ 变成 $0$；
• 3 l r 询问 $[l,r]$ 区间内总共有多少个 $1$；
• 4 l r 询问 $[l,r]$ 区间内最多有多少个连续的 $1$。

对于每一种询问操作，lxhgww 都需要给出回答，聪明的程序员们，你们能帮助他吗？

输入格式

第一行两个正整数 $n,m$，表示序列长度与操作个数。
第二行包括 $n$ 个数，表示序列的初始状态。
接下来 $m$ 行，每行三个整数，表示一次操作。

输出格式

对于每一个询问操作，输出一行一个数，表示其对应的答案。

输入输出样例 #1

输入 #1

10 100 0 0 1 1 0 1 0 1 11 0 23 0 52 2 24 0 40 3 62 3 74 2 81 0 50 5 63 3 9

输出 #1

5265

说明/提示

【数据范围】
对于 $30\%$ 的数据，$1\le n,m\le 1000$；
对于$100\%$ 的数据， 1≤n,m≤1 0 5 1\\le n,m \\le 10^5 1≤n,m≤105。

思路：

这道题就是相当于范围重置和范围取反，维护连续 1 的最长子串长度，由于设计到范围取反，因此我们不单单要维护连续 1 的最长长度，也需要维护连续 0 的最长长度，因此定义 6 个数组 pre1、suf1、len1、pre0、suf0、len0，前三个数组就是用来维护连续 1 的最长长度，后面三个数组用来维护连续 0 的最长长度。

接下来操作 0 和 操作 1 要维护范围更新，因此需要定义 update 和 change 数组来进行懒更新，然后取反也要定义 reverse 来懒更新，最后 sum 数组来维护区间 1 的累加和，用来解决操作 3，那么这几个数组懒更新的时候如何处理。

首先是 sum 数组，如果是范围修改，比如某个范围修改成 0，那么 sum[i] = 0，如果修改成 1，那么 sum[i] = cnt，cnt 就是这个范围的数字个数，所以可以 O(1) 时间完成更新，而范围取反就是 sum[i] = cnt - sum[i]。然后就是上面这 6 个数组，范围更新如果更新成 0，那么 pre0[i] = suf0[i] = len0[i] = cnt，pre1[i] = suf1[i] = len1[i] = 0，如果更新成 1，那么 pre0[i] = suf0[i] = len0[i] = 0，pre1[i] = suf1[i] = len1[i] = cnt。

然后是范围反转，上面说过 sum[i] 的更新了，而 pre、suf、len 三个就是 0 和 1 的交换，使用下面的方法。

private static void lazyReverse(int i, int cnt) { sum[i] = cnt - sum[i]; reverse(len0, len1, i); reverse(pre0, pre1, i); reverse(suf0, suf1, i); reverse[i] = !reverse[i];}private static void reverse(int[] arr0, int[] arr1, int i) { int temp = arr0[i]; arr0[i] = arr1[i]; arr1[i] = temp;}

最后来看下整体的 code。

import java.io.*;public class Main { public static int MAXN = 100001; public static int[] arr = new int[MAXN]; public static int[] sum = new int[MAXN << 2]; public static int[] len0 = new int[MAXN << 2]; public static int[] pre0 = new int[MAXN << 2]; public static int[] suf0 = new int[MAXN << 2]; public static int[] len1 = new int[MAXN << 2]; public static int[] pre1 = new int[MAXN << 2]; public static int[] suf1 = new int[MAXN << 2]; public static int[] change = new int[MAXN << 2]; public static boolean[] update = new boolean[MAXN << 2]; public static boolean[] reverse = new boolean[MAXN << 2]; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StreamTokenizer in = new StreamTokenizer(br); PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); in.nextToken(); int n = (int) in.nval; in.nextToken(); int m = (int) in.nval; for (int i = 1; i <= n; i++) { in.nextToken(); arr[i] = (int) in.nval; } build(1, n, 1); for (int i = 1, op, jobl, jobr; i <= m; i++) { in.nextToken(); op = (int) in.nval; in.nextToken(); jobl = (int) in.nval + 1; in.nextToken(); jobr = (int) in.nval + 1; if (op == 0) { update(jobl, jobr, 0, 1, n, 1); } else if (op == 1) { update(jobl, jobr, 1, 1, n, 1); } else if (op == 2) { reverse(jobl, jobr, 1, n, 1); } else if (op == 3) { out.println(querySum(jobl, jobr, 1, n, 1)); } else { out.println(queryLongest(jobl, jobr, 1, n, 1)[0]); } } out.flush(); out.close(); br.close(); } private static int[] queryLongest(int jobl, int jobr, int l, int r, int i) { if (jobl <= l && r <= jobr) { return new int[]{len1[i], pre1[i], suf1[i]}; } int mid = (l + r) >> 1; down(i, mid - l + 1, r - mid); if (jobr <= mid) { return queryLongest(jobl, jobr, l, mid, i << 1); } if (jobl > mid) { return queryLongest(jobl, jobr, mid + 1, r, i << 1 | 1); } int[] l3 = queryLongest(jobl, jobr, l, mid, i << 1); int[] r3 = queryLongest(jobl, jobr, mid + 1, r, i << 1 | 1); int lenMax = Math.max(l3[0], Math.max(r3[0], l3[2] + r3[1])); int preMax = l3[0] < mid - Math.max(jobl, l) + 1 ? l3[1] : l3[1] + r3[1]; int sufMax = r3[0] < Math.min(jobr, r) - mid ? r3[2] : l3[2] + r3[2]; return new int[]{lenMax, preMax, sufMax}; } private static int querySum(int jobl, int jobr, int l, int r, int i) { if (jobl <= l && r <= jobr) { return sum[i]; } int mid = l + ((r - l) >> 1); down(i, mid - l + 1, r - mid); int res = 0; if (jobl <= mid) { res += querySum(jobl, jobr, l, mid, i << 1); } if (jobr > mid) { res += querySum(jobl, jobr, mid + 1, r, i << 1 | 1); } return res; } private static void reverse(int jobl, int jobr, int l, int r, int i) { if (jobl <= l && r <= jobr) { lazyReverse(i, r - l + 1); } else { int mid = l + ((r - l) >> 1); down(i, mid - l + 1, r - mid); if (jobl <= mid) { reverse(jobl, jobr, l, mid, i << 1); } if (jobr > mid) { reverse(jobl, jobr, mid + 1, r, i << 1 | 1); } up(i, mid - l + 1, r - mid); } } private static void update(int jobl, int jobr, int jobv, int l, int r, int i) { if (jobl <= l && r <= jobr) { lazyUpdate(i, jobv, r - l + 1); } else { int mid = l + ((r - l) >> 1); down(i, mid - l + 1, r - mid); if (jobl <= mid) { update(jobl, jobr, jobv, l, mid, i << 1); } if (jobr > mid) { update(jobl, jobr, jobv, mid + 1, r, i << 1 | 1); } up(i, mid - l + 1, r - mid); } } private static void build(int l, int r, int i) { if (l == r) { sum[i] = arr[l]; pre0[i] = len0[i] = suf0[i] = arr[l] == 0 ? 1 : 0; pre1[i] = len1[i] = suf1[i] = arr[l] == 0 ? 0 : 1; } else { int mid = l + ((r - l) >> 1); build(l, mid, i << 1); build(mid + 1, r, i << 1 | 1); up(i, mid - l + 1, r - mid); } reverse[i] = false; update[i] = false; } private static void up(int i, int ln, int rn) { int l = i << 1; int r = i << 1 | 1; sum[i] = sum[i << 1] + sum[i << 1 | 1]; len0[i] = Math.max(Math.max(len0[l], len0[r]), suf0[l] + pre0[r]); pre0[i] = pre0[l] < ln ? pre0[l] : pre0[l] + pre0[r]; suf0[i] = suf0[r] < rn ? suf0[r] : suf0[l] + suf0[r]; len1[i] = Math.max(Math.max(len1[l], len1[r]), suf1[l] + pre1[r]); pre1[i] = pre1[l] < ln ? pre1[l] : pre1[l] + pre1[r]; suf1[i] = suf1[r] < rn ? suf1[r] : suf1[l] + suf1[r]; } private static void down(int i, int ln, int rn) { // 由于懒更新会把懒重置给覆盖掉, 所以先处理懒更新的逻辑 if (update[i]) { lazyUpdate(i << 1, change[i], ln); lazyUpdate(i << 1 | 1, change[i], rn); update[i] = false; } // 如果有 reverse 的再处理 reverse, 免得这个 reverse 被上面的 update 给覆盖掉 if (reverse[i]) { lazyReverse(i << 1, ln); lazyReverse(i << 1 | 1, rn); reverse[i] = false; } } private static void lazyReverse(int i, int cnt) { sum[i] = cnt - sum[i]; reverse(len0, len1, i); reverse(pre0, pre1, i); reverse(suf0, suf1, i); reverse[i] = !reverse[i]; } private static void reverse(int[] arr0, int[] arr1, int i) { int temp = arr0[i]; arr0[i] = arr1[i]; arr1[i] = temp; }// 懒更新会把懒反转都给重置掉, 因为懒更新会把这个范围的所有数字都修改成 1 或者 0，修改之后 reverse 跟没 reverse 是一样的 private static void lazyUpdate(int i, int v, int cnt) { sum[i] = v * cnt; len0[i] = pre0[i] = suf0[i] = v == 0 ? cnt : 0; len1[i] = pre1[i] = suf1[i] = v == 1 ? cnt : 0; update[i] = true; change[i] = v; // 重置 reverse 操作 reverse[i] = false; }}

4. 洛谷 P6492 [COCI 2010/2011 #6] STEP

P6492 [COCI 2010/2011 #6] STEP

题目描述

给定一个长度为 $n$ 的字符序列 $a$，初始时序列中全部都是字符 L。

有 $q$ 次修改，每次给定一个 $x$，若 a x a_x ax​ 为 L，则将 a x a_x ax​ 修改成 R，否则将 a x a_x ax​ 修改成 L。

对于一个只含字符 L，R 的字符串 $s$，若其中不存在连续的 L 和 R，则称 $s$ 满足要求。

每次修改后，请输出当前序列 $a$ 中最长的满足要求的连续子串的长度。

输入格式

第一行有两个整数，分别表示序列的长度 $n$ 和修改操作的次数 $q$。

接下来 $q$ 行，每行一个整数，表示本次修改的位置 $x$。

输出格式

对于每次修改操作，输出一行一个整数表示修改 $a$ 中最长的满足要求的子串的长度。

输入输出样例 #1

输入 #1

6 224

输出 #1

35

输入输出样例 #2

输入 #2

6 541126

输出 #2

33356

说明/提示

数据规模与约定

对于全部的测试点，保证 1≤n,q≤2×1 0 5 1 \\leq n, q \\leq 2 \\times 10^5 1≤n,q≤2×105，$1\le x\le n$。

思路：

这道题跟上面维护最长连续 1 的最长长度差不多，只是这里换成了维护 LRLR… 交替子串的最长长度，还是一样定义三个数组 pre、len、suf 来存储 最长前缀、最长长度、最长后缀。

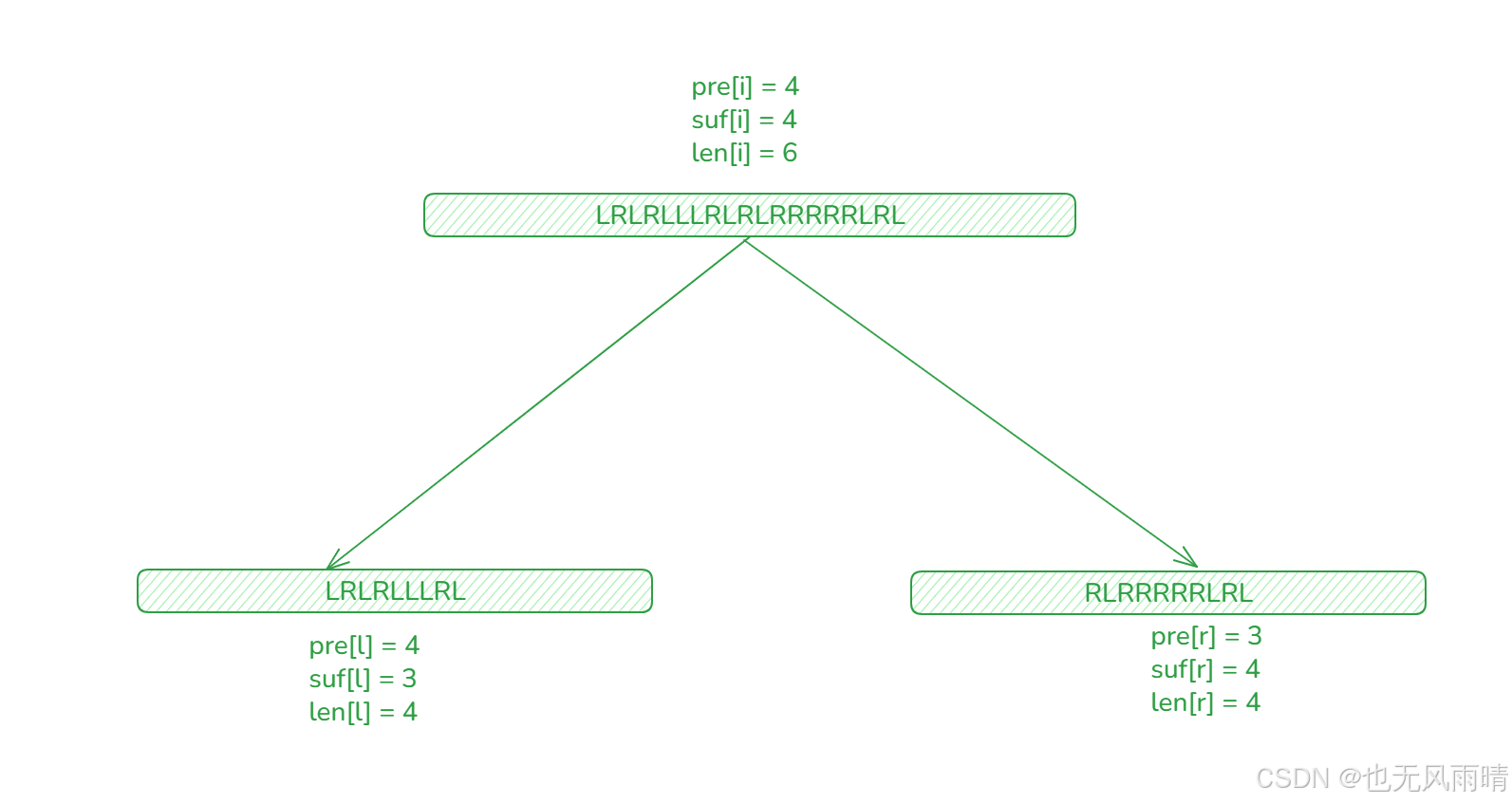
思路跟上面第一小节介绍的是差不多的，这里求父结点的 pre、suf、len 值可以通过下面的方法来求。

private static void up(int l, int r, int i) { len[i] = Math.max(len[i << 1], len[i << 1 | 1]); pre[i] = pre[i << 1]; suf[i] = suf[i << 1 | 1]; int mid = l + ((r - l) >> 1); int ln = mid - l + 1; int rn = r - mid; if (arr[mid] != arr[mid + 1]) { len[i] = Math.max(len[i], suf[i << 1] + pre[i << 1 | 1]); if (pre[i] == ln) { pre[i] += pre[i << 1 | 1]; } if (suf[i] == rn) { suf[i] += suf[i << 1]; } }}

还是一样，这里求出中点，然后判断下 arr[mid] != arr[mid + 1]，如果不相同说明左节点的后缀和右节点的前缀能连到一起，这种情况下才更新 len[i] = Math.max(len[i], suf[i << 1] + pre[i << 1 | 1])，pre 和 suf 也是一样的，当 arr[mid] != arr[mid + 1] 才考虑如果 pre[i] == len 的情况下要不要跟右边的拼在一起，比如下面的情况就拼不起来。

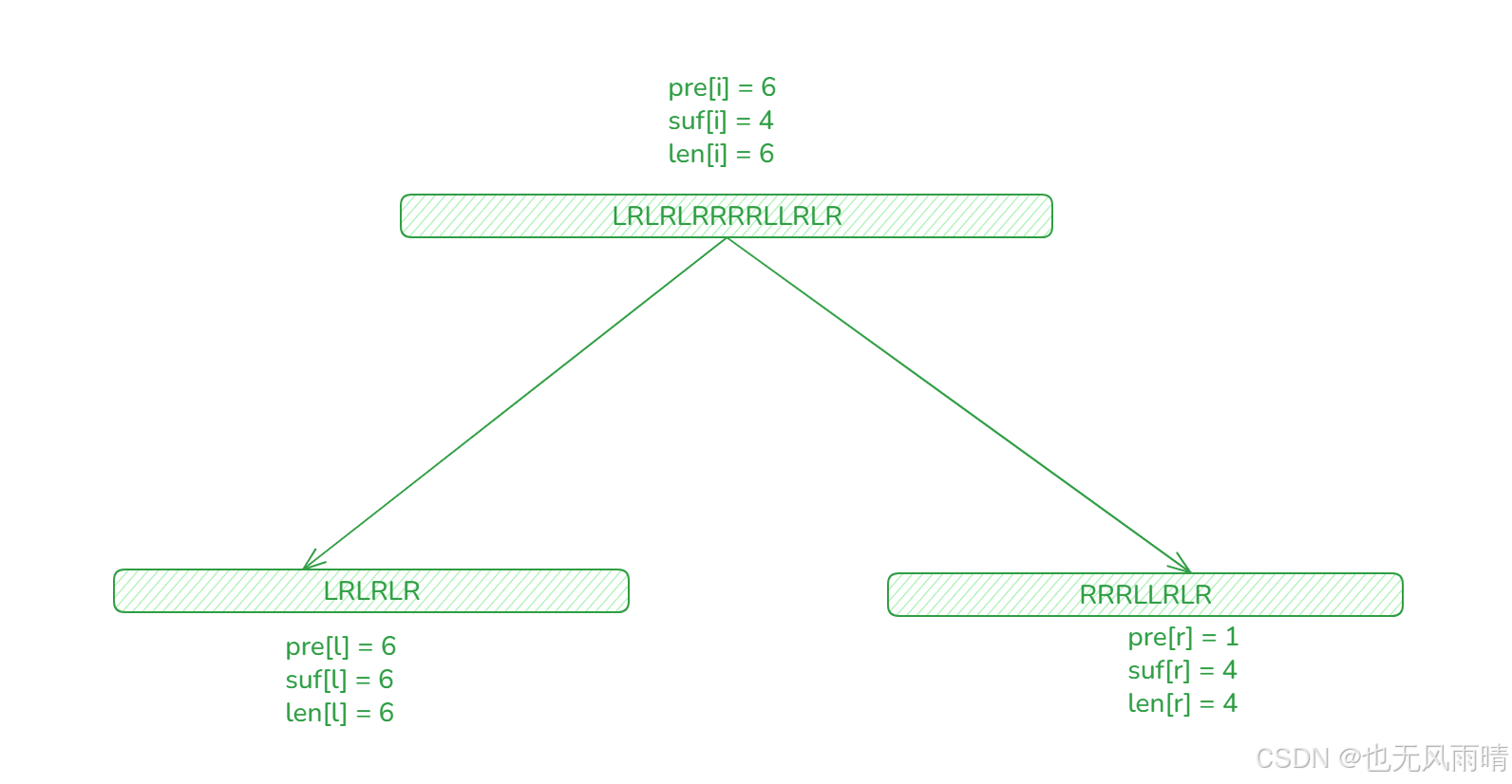
这种情况下由于 mid 和 mid + 1 都是 R，那么父结点的 pre 就不用拼接了，这是因为 pre 和 suf 和 len 交替子串最少都是 1，不像上面的最长连续 1 可以为 0，下面再来看下 code。

import java.io.*;public class Main { public static int MAXN = 200001; public static int[] arr = new int[MAXN]; public static int[] len = new int[MAXN << 2]; public static int[] pre = new int[MAXN << 2]; public static int[] suf = new int[MAXN << 2]; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StreamTokenizer in = new StreamTokenizer(br); PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); in.nextToken(); int n = (int) in.nval; in.nextToken(); int q = (int) in.nval; build(1, n, 1); for (int i = 1; i <= q; i++) { in.nextToken(); int index = (int) in.nval; reverse(index, 1, n, 1); out.println(len[1]); } out.flush(); out.close(); br.close(); } private static void reverse(int jobi, int l, int r, int i) { if(l == r){ arr[jobi] ^= 1; } else { int mid = l + ((r - l) >> 1); if (jobi <= mid) { reverse(jobi, l, mid, i << 1); } else { reverse(jobi, mid + 1, r, i << 1 | 1); } up(l, r, i); } } private static void build(int l, int r, int i) { if (l == r) { len[i] = pre[i] = suf[i] = 1; } else { int mid = l + ((r - l) >> 1); build(l, mid, i << 1); build(mid + 1, r, i << 1 | 1); up(l, r, i); } } private static void up(int l, int r, int i) { len[i] = Math.max(len[i << 1], len[i << 1 | 1]); pre[i] = pre[i << 1]; suf[i] = suf[i << 1 | 1]; int mid = l + ((r - l) >> 1); int ln = mid - l + 1; int rn = r - mid; if (arr[mid] != arr[mid + 1]) { len[i] = Math.max(len[i], suf[i << 1] + pre[i << 1 | 1]); if (pre[i] == ln) { pre[i] += pre[i << 1 | 1]; } if (suf[i] == rn) { suf[i] += suf[i << 1]; } } }}

5. 洛谷 P1503 鬼子进村

P1503 鬼子进村

题目背景

小卡正在新家的客厅中看电视。电视里正在播放放了千八百次依旧重播的《亮剑》，剧中李云龙带领的独立团在一个县城遇到了一个鬼子小队，于是独立团与鬼子展开游击战。

题目描述

县城里有 $n$ 个用地道相连的房子，第 $i$ 个只与第 $i-1$ 和第 $i+1$ 个相连。这时有 $m$ 个消息依次传来：

1. 若消息为 D x：鬼子将 $x$ 号房子摧毁了，地道被堵上。

2. 若消息为 R：村民们将鬼子上一个摧毁的房子修复了。

3. 若消息为 Q x：有一名士兵被围堵在 $x$ 号房子中。

李云龙收到信息很紧张，他想知道每一个被围堵的士兵能够到达的房子有几个。

输入格式

第一行两个整数 $n,m$。

接下来 $m$ 行，有如题目所说的三种信息共 $m$ 条。

输出格式

对于每一个被围堵的士兵，输出该士兵能够到达的房子数。

输入输出样例 #1

输入 #1

7 9D 3D 6D 5Q 4Q 5RQ 4RQ 4

输出 #1

1024

说明/提示

1≤n,m≤5×1 0 4 1\\leq n,m\\leq 5\\times 10^4 1≤n,m≤5×104。

若士兵被围堵在摧毁了的房子中，那只能等死了。。。。。。

思路：

首先一开始有 n 个房子连成一排，然后每个房子两边都有地道，意思就是如果当前下标为 1，并且旁边的 i - 1 和 i + 1 也是 1，就可以把这个 i - 1，i，i + 1 看成一个整体。

有几个操作，首先是 D x，这个操作意思是将 x 下标的值标为 0，然后是 R，R 是把上一次设置为 0 的房子重新设置为 1，最后是 Q x，就是查询包含整个房子在内的最长连续 1 的长度。

那这么看就还是一样需要维护最长连续 1 的长度了，不过有点特殊的是这里我们使用 pre 和 suf 数组就可以了，因为要求的是包括 x 在内的最长连续 1 的长度，而不是某个范围的最长连续 1 的长度，比如下面的情况。

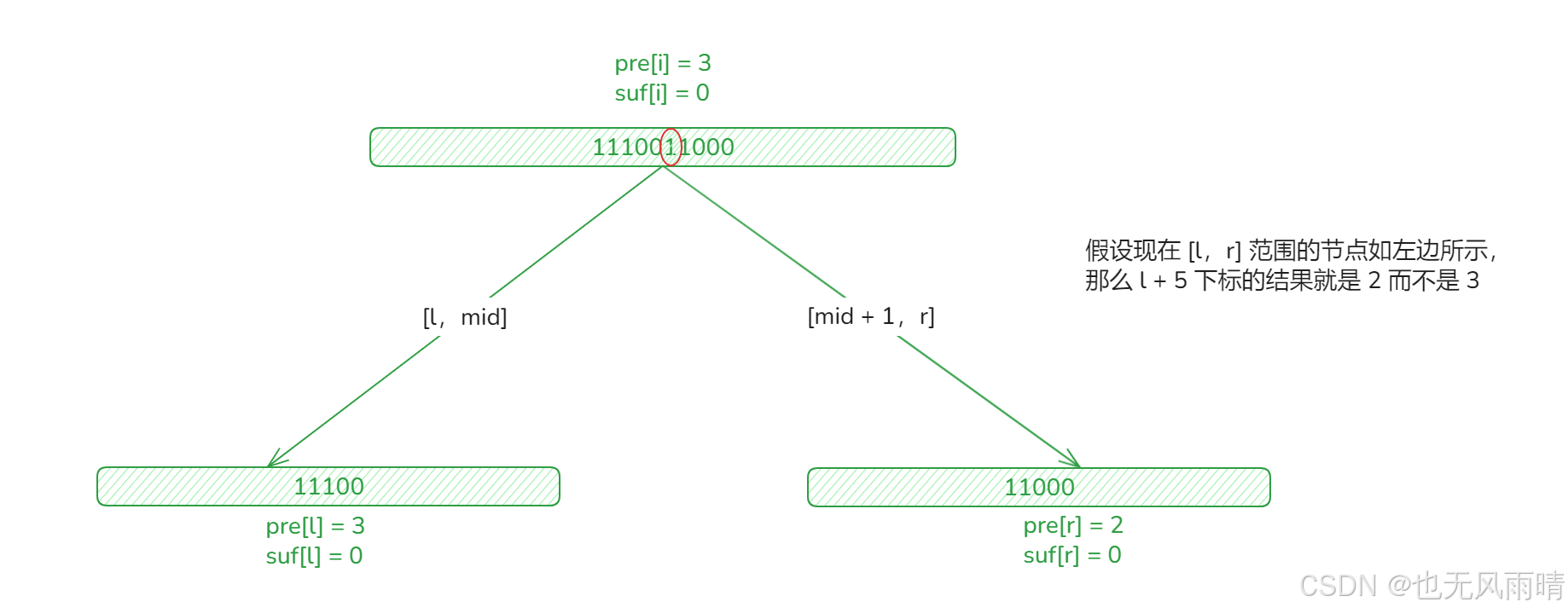
由于求出来的连续 1 的长度不是最长连续子串长度，所以不能像上面几个题目那样求，那么这个要如何处理，还是一样遍历，这里我们从中点开始入手，下面原数组下标我画成了从 0 开始，线段树还是从 1 开始算的。

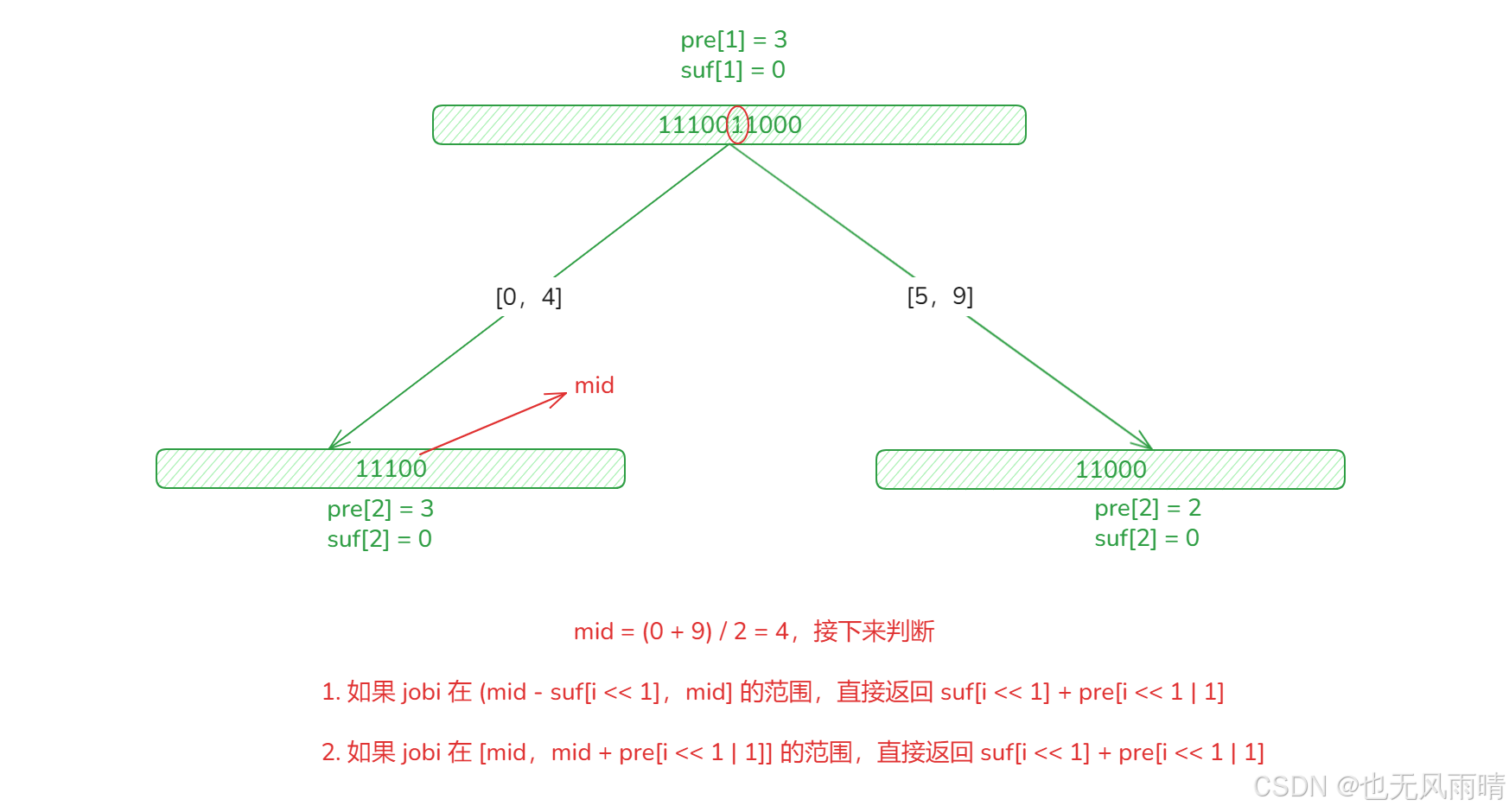
直接从 mid 开始判断，如果在 (mid - suf[i << 1]，mid] 这个范围，那么直接返回 suf[i << 1] + pre[i << 1 | 1]，这是因为如果在这个范围内，那么说明这个范围全部都是 1，而且包含了我们要求的 x，也就是从 x 出发最少都能到 mid - suf[i << 1] + 1 的位置，因此直接返回 suf[i << 1] + pre[i << 1 | 1]，为什么是 + 1，看上面图就可以了，mid 在左节点的最后一个位置，所以假设（上面图左节点最后一个数字换成 1）现在 mid = 4，然后 suf[i << 1] = 1，这时候 4 - 1 = 3，如果是包含了 mid - suf[i << 1]，那么假设这时候 x = 3，这种情况下由于下标 3 是 0，是不可以跟后面的连成一片的，这种情况下返回 suf[i << 1] + pre[i << 1 | 1] 就有问题了，因此左端点不能要，右边也是同理，然后看下 query 的 code，可以自己推导下就知道了。

private static int query(int x, int l, int r, int i) { if (l == r) { return pre[i]; } int mid = l + ((r - l) >> 1); if (x <= mid) { // 如果 x 在 (mid - suf[i << 1, mid] 范围 if (x > mid - suf[i << 1]) { // 返回左节点的后缀 + 右节点的前缀 return suf[i << 1] + pre[i << 1 | 1]; } else { // 这里就继续到前面去找 return query(x, l, mid, i << 1); } } else { // 如果 x 在 [mid, mid + pre[i << 1 | 1]] 范围 if(x <= mid + pre[i << 1 | 1]){ // 返回左节点的后缀 + 右节点的前缀 return suf[i << 1] + pre[i << 1 | 1]; } else { // 否则就继续到右边二分查找 return query(x, mid + 1, r, i << 1 | 1); } }}

然后再来看下如何将上一次摧毁的房子恢复，这种情况下可以使用栈结构来完成，每一次调用 D x 就把 x 入栈，然后 stackSize++，然后调用 R 就把 --stackSize 下标的值弹出来恢复，下面看下整体 code。

import java.io.*;public class Main { public static int MAXN = 50001; public static int[] pre = new int[MAXN << 2]; public static int[] suf = new int[MAXN << 2]; public static int[] stack = new int[MAXN]; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StreamTokenizer in = new StreamTokenizer(br); PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); while (in.nextToken() != StreamTokenizer.TT_EOF) { int n = (int) in.nval; in.nextToken(); int m = (int) in.nval; build(1, n, 1); String op; int stackSize = 0; for (int i = 1, x; i <= m; i++) { in.nextToken(); op = in.sval; if (op.equals(\"D\")) {  in.nextToken();  x = (int) in.nval;  // 将 x 下标的值更新为 0  update(x, 0, 1, n, 1);  // 入栈  stack[stackSize++] = x; } else if (op.equals(\"R\")) { // 弹出下标值更新为 1  update(stack[--stackSize], 1, 1, n, 1); } else {  in.nextToken();  x = (int) in.nval;  // 查询包括 x 在内的最长连续 1   out.println(query(x, 1, n, 1)); } } } out.flush(); out.close(); br.close(); }private static int query(int x, int l, int r, int i) { if (l == r) { return pre[i]; } int mid = l + ((r - l) >> 1); if (x <= mid) { // 如果 x 在 (mid - suf[i << 1, mid] 范围 if (x > mid - suf[i << 1]) { // 返回左节点的后缀 + 右节点的前缀 return suf[i << 1] + pre[i << 1 | 1]; } else { // 这里就继续到前面去找 return query(x, l, mid, i << 1); } } else { // 如果 x 在 [mid, mid + pre[i << 1 | 1]] 范围 if(x <= mid + pre[i << 1 | 1]){ // 返回左节点的后缀 + 右节点的前缀 return suf[i << 1] + pre[i << 1 | 1]; } else { // 否则就继续到右边二分查找 return query(x, mid + 1, r, i << 1 | 1); } }} private static void update(int x, int jobv, int l, int r, int i) { if (l == r) { pre[i] = jobv; suf[i] = jobv; } else { int mid = l + ((r - l) >> 1); if (x <= mid) { update(x, jobv, l, mid, i << 1); } else { update(x, jobv, mid + 1, r, i << 1 | 1); } up(l, r, i); } } private static void build(int l, int r, int i) { if (l == r) { pre[i] = suf[i] = 1; } else { int mid = l + ((r - l) >> 1); build(l, mid, i << 1); build(mid + 1, r, i << 1 | 1); up(l, r, i); } } private static void up(int l, int r, int i) { pre[i] = pre[i << 1]; suf[i] = suf[i << 1 | 1]; int mid = l + ((r - l) >> 1); if (pre[i << 1] == mid - l + 1) { pre[i] += pre[i << 1 | 1]; } if (suf[i << 1 | 1] == r - mid) { suf[i] += suf[i << 1]; } }}

6. P2894 [USACO08FEB] Hotel G

P2894 [USACO08FEB] Hotel G

题目描述

对一家有 $n$ 个房间（编号为 $1\sim n$，开始都为空房）的宾馆维护以下操作：

• 查询房间：你需要在 $1,2,\dots ,n$ 房间中找到长度为 $x$ 的连续空房。若找得到，在这 $x$ 个空房间中住上人。
• 退房：房间号 $x\sim x+y-1$ 退房，即让房间为空。

输入格式

第一行输入 $n,m$，$n$ 代表有 $n$ 个房间 $(1\le n\le 50,000)$，编号为 $1\sim n$，开始都为空房，$m$ 表示以下有 $m$ 行操作 $(1\le m<50,000)$，以下每行先输入一个数 $i$，表示一种操作：

若 $i$ 为 $1$，表示查询房间，再输入一个数 $x$。

若 $i$ 为 $2$，表示退房，再输入两个数 $x,y$。

输出格式

对每个输入 $1$，输出连续 $x$ 个房间中左端的房间号，尽量让这个房间号最小，若找不到长度为 $x$ 的连续空房，输出 $0$。

输入输出样例 #1

输入 #1

10 61 31 31 31 32 5 51 6

输出 #1

14705

思路：

这道题主要就是范围更新维护连续最长 1，因此需要三个数组 len、pre、suf，然后范围更新需要两个数组 update、change。

操作 2 意思就是把 [x，x + y - 1] 范围下标设置为 0，操作 1 意思是判断整个数组上有没有长度 >= x 的子数组，如果有多个就返回最左边的子数组的最左的编号 i，并且从整个编号开始将 [i，i + x - 1] 范围修改为 1，表示入住了。

这道题和上面第 5 小节的题目差不多，首先判断数组上有没有长度 >= x 的子数组，这个直接通过 len[1] 判断就行，然后就是最核心的 query 方法，如何查询出满足 >= x 的最左区域的最左边的值。

private static int query(int x, int l, int r, int i) { if (l == r) { return l; } int mid = l + ((r - l) >> 1); down(l, r, i); // 如果左节点上面有符合的区域 if (len[i << 1] >= x) { // 往左边去遍历 return query(x, l, mid, i << 1); } // 如果左边没有, 那么看看中间拼起来能不能满足 if (suf[i << 1] + pre[i << 1 | 1] >= x) { // 如果可以满足就直接返回中间这个区域的左端点 return mid - suf[i << 1] + 1; } // 再去右边去找 return query(x, mid + 1, r, i << 1 | 1);}

由于要找到最左的区域，所以一进来判断就是先判断左边的节点有没有符合条件的区域，再判断中间拼起来的区域能不能满足条件，如果都没有再去右边找，好了，下面看下全部的 code。

import java.io.*;public class Main { public static int MAXN = 50001; public static int[] len = new int[MAXN << 2]; public static int[] pre = new int[MAXN << 2]; public static int[] suf = new int[MAXN << 2]; public static boolean[] update = new boolean[MAXN << 2]; public static int[] change = new int[MAXN << 2]; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StreamTokenizer in = new StreamTokenizer(br); PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); in.nextToken(); int n = (int) in.nval; in.nextToken(); int m = (int) in.nval; build(1, n, 1); for (int i = 1; i <= m; i++) { in.nextToken(); int op = (int) in.nval; if (op == 1) { in.nextToken(); int x = (int) in.nval; int idx = 0; if (len[1] < x) {  out.println(idx); } else {  // 到这里肯定能找到一个区域满足长度 >= x，所以查询到的  idx = query(x, 1, n, 1);  update(1, idx, idx + x - 1, 1, n, 1);  out.println(idx); } } else { in.nextToken(); int x = (int) in.nval; in.nextToken(); int y = (int) in.nval; // 不能超过数组长度  update(0, x, Math.min(x + y - 1, n), 1, n, 1); } } out.flush(); out.close(); br.close(); } private static int query(int x, int l, int r, int i) { if (l == r) { return l; } int mid = l + ((r - l) >> 1); down(l, r, i); // 如果左节点上面有符合的区域 if (len[i << 1] >= x) { // 往左边去遍历 return query(x, l, mid, i << 1); } // 如果左边没有, 那么看看中间拼起来能不能满足 if (suf[i << 1] + pre[i << 1 | 1] >= x) { // 如果可以满足就直接返回中间这个区域的左端点 return mid - suf[i << 1] + 1; } // 再去右边去找 return query(x, mid + 1, r, i << 1 | 1); } private static void update(int jobv, int jobl, int jobr, int l, int r, int i) { if (jobl <= l && r <= jobr) { lazyUpdate(jobv, i, r - l + 1); } else { down(l, r, i); int mid = l + ((r - l) >> 1); if (jobl <= mid) { update(jobv, jobl, jobr, l, mid, i << 1); } if (jobr > mid) { update(jobv, jobl, jobr, mid + 1, r, i << 1 | 1); } up(l, r, i); } } private static void down(int l, int r, int i) { if (update[i]) { int mid = l + ((r - l) >> 1); lazyUpdate(change[i], i << 1, mid - l + 1); lazyUpdate(change[i], i << 1 | 1, r - mid); change[i] = 0; update[i] = false; } } private static void lazyUpdate(int jobv, int i, int ln) { change[i] = jobv; update[i] = true; pre[i] = suf[i] = len[i] = jobv == 0 ? ln : 0; } private static void build(int l, int r, int i) { if (l == r) { len[i] = pre[i] = suf[i] = 1; } else { int mid = l + ((r - l) >> 1); build(l, mid, i << 1); build(mid + 1, r, i << 1 | 1); up(l, r, i); } update[i] = false; change[i] = 0; } private static void up(int l, int r, int i) { len[i] = Math.max(len[i << 1], Math.max(len[i << 1 | 1], suf[i << 1] + pre[i << 1 | 1])); pre[i] = pre[i << 1]; suf[i] = suf[i << 1 | 1]; int mid = l + ((r - l) >> 1); if (pre[i] == mid - l + 1) { pre[i] += pre[i << 1 | 1]; } if (suf[i] == r - mid) { suf[i] += suf[i << 1]; } }}

如有错误，欢迎指出！！！