峁诗松1.2 概率论的定义及其确定方法

1.2.1 概率的公理化定义

设 $(\Omega ,\mathcal{F})$ 为一可测空间，若实值映射满足以下三条公理：

1. 非负性公理：若 $A\in \mathcal{F}$ ，则 $P(A)⩾0$ ;
2. 正则性公理：$P(\Omega )=1$ ;
3. 可列可加性公理：若 A 1 , A 2 , … , A n , … A_{1},A_{2},\\dots,A{n},\\dots A1​,A2​,…,An,… 互不相容，则
   P ( ∪ ∞ i = 1 A i )= ∑ i = 1 ∞ P ( A i ) . (1.2.1) \\begin{align} P \\left( \\underset{i=1}{\\overset{\\infty}{\\cup}}A_i \\right) = \\sum_{i=1}^{\\infty}{P \\left( A_i \\right)} . \\end{align} \\tag{1.2.1}P(i=1∪∞​Ai​)=i=1∑∞​P(Ai​).​(1.2.1)
   则称 $P(A)$ 为事件 $A$ 的概率，称 $(\Omega ,\mathcal{F},P)$ 为概率空间。

1.2.2 排列与组合公式

乘法原理

如果某件事需经过 $k$ 个步骤才能完成，做第一步有 m 1 m_{1} m1​ 种方法，做第一步有 m 2 m_{2} m2​ 种方法，$\cdots \cdots$,做第 $k$ 步有 m k m_{k} mk​ 种方法，那么完成这件事共有 m 1 × m 2 ×⋯× m k m_{1} \\times m_{2} \\times \\dots \\times m_{k} m1​×m2​×⋯×mk​ 种方法。

加法原理

如果某件事可由 $k$ 类不同途径之一去完成，在第一类途径中有 m 1 m_{1} m1​ 种完成方法，在第二类途径中有 m 2 m_{2} m2​ 种完成方法，$\cdots \cdots$，在第 $k$ 类途径中有 m k m_{k} mk​ 种完成方法，那么完成这件事共有 m 1 + m 2 +...+ m k m_{1} + m_{2} + ... + m_{k} m1​+m2​+...+mk​ 种方法。

排列

从 $n$ 个不同元素中任取 $r\left(r⩽n\right)$ 个元素排成一列（考虑元素先后次序）。称次为一个排列，此种排列的总数计为 P n r P_{n}^{r} Pnr​。
P n r = n × ( n − 1 ) × ⋯ × ( n − r + 1 ) = n ! ( n − r ) ! . (1.2.2) \\begin{align} P_{n}^{r} = n\\times \\left( n-1 \\right) \\times \\dots \\times \\left( n-r+1 \\right) = \\frac{n!}{\\left( n-r \\right) !}. \\end{align} \\tag{1.2.2} Pnr​=n×(n−1)×⋯×(n−r+1)=(n−r)!n!​.​(1.2.2)
若 $r=n$ ，则成为全排列，记为 P n P_{n} Pn​，显然，全排列 P n =n! P_{n} = n! Pn​=n!。

重复排列

从 $n$ 个不同元素中每次取出一个，放回然后再取下一个，如此连续取 $r$ 次所得排列称为重复排列，此种重复排列数共有 n r n^{r} nr 个。注意：这里允许 $r>n$ 。

组合

从 $n$ 个不同元素中任取 $r(r⩽n)$ 个元素并成一组（不考虑元素间的先后次序），称此为一个组合，此种组合的总数记为 ( n r ) \\binom{n}{r} (rn​) 或 C n r C_{n}^{r} Cnr​ 。
( n r) = P n r r ! = n × ( n − 1 ) × ⋯ × ( n − r + 1 ) r ! = n ! r ! ( n − r ) ! . (1.2.3) \\begin{align} \\binom{n}{r} = \\frac{P_{n}^{r}} {r!} = \\frac {n\\times \\left( n-1 \\right) \\times \\dots \\times \\left( n-r+1 \\right)} {r!} = \\frac{n!} {r! \\left( n-r \\right)!}. \\end{align} \\tag{1.2.3} (rn​)=r!Pnr​​=r!n×(n−1)×⋯×(n−r+1)​=r!(n−r)!n!​.​(1.2.3)
在此规定 $0!=1$ 与 ( n r ) =1. \\binom{n}{r} = 1. (rn​)=1. 组合具有性质：
( n r ) = ( n n − r ) . \\binom{n}{r} = \\binom{n}{n-r}. (rn​)=(n−rn​).

重复组合（隔板法）

隔板法等方法的初步讲解

从 $n$ 个不同元素中每次取出一个，放回后再取下一个，如此连续取 $r$ 次所得的组合成为重复组合，此种重复组合总数为 ( n + r − 1 r ) . \\binom{n+r-1}{r}. (rn+r−1​). 注意：这里也允许 $r>n$ 。

从 $n$ 个不同元素中每次取出一个，放回后再取下一个，如此连续取 $r$ 次所得的组合成为重复组合，此种重复组合总数为 ( n + r − 1 r ) . \\binom{n+r-1}{r}. (rn+r−1​). 注意：这里也允许 $r>n$ 。

解释

重复组合数可以由以下考虑得出：
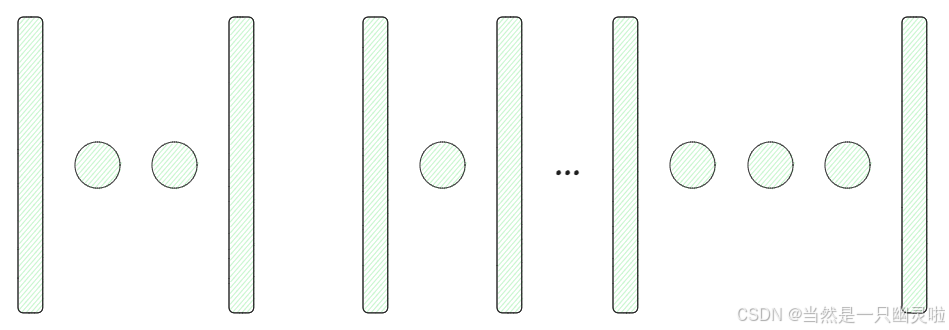
将此 $n$ 个元素画成 $n$ 个盒子（用 $n+1$ 个挡板示意，如下图所示），如果第 $i$ 个元素取到过一次，将用 一个圆圈（后续书写将使用“⭕”来代替） 来代表选取到过这个盒子一次。

下图表示：
第一个元素取到过 $2$ 次，第二个元素取到过 $0$ 次，第三个元素取到过 $1$ 次 $\cdots \cdots$， 第 $n$ 个元素取到过 $3$ 次。
因为共取 $r$ 次，所以总共有 $r$ 个 “⭕”，$n+1$ 个挡板。如此所有的 $r$ 个“⭕”和 $n+1$ 个挡板中除了两端的那两个挡板不可动外，共有 $n+r-1$ 个“⭕”和挡板可以随意放置，不同的放置表示不同的取法。
因此重复组合数就等于在此 $n+r-1$ 个位置上任选 $r$ 个来放置“⭕”，或此 $n+r-1$ 个位置上任选 $n-1$ 个放挡板。其中： ( n − 1 + r r ) = ( n − 1 + r n − 1) ⟹ ( n + r − 1 r ) = ( n + r − 1 n − 1) \\binom{n-1+r}{r} = \\binom{n-1+r}{n-1} \\Longrightarrow \\binom{n+r-1}{r} = \\binom{n+r-1}{n-1} (rn−1+r​)=(n−1n−1+r​)⟹(rn+r−1​)=(n−1n+r−1​) 。

1.2.3 确定概率的频率方法

确定概率的频率方法是在大量重复试验中，用频率的稳定值去获取概率的一种方法，其基本思想是：

1. 与考察事件 $A$ 有关的随机现象可大量重复进行。
2. 在 $n$ 次重复实验中，记 $n\left(A\right)$ 为事件 $A$ 出现的次数，又称 $n\left(A\right)$ 为事件 $A$ 的频数，称：
   f n ( A )= n ( A ) n (1.2.4) \\begin{align} f_{n}\\left( A \\right) = \\frac{n\\left( A \\right)}{n} \\end{align} \\tag{1.2.4}fn​(A)=nn(A)​​(1.2.4)
   为事件 $A$ 出现的频率。
   容易验证：用频率方法确定的概率满足公理化定义，它的正则性是显然的，而可加性只需注意到：当 $A$ 和 $B$ 互不相容时，计算 $A\cup B$ 的频数可以分别计算 $A$ 的频数和 $B$ 的频数，然后再相加，这意味着 $n\left(A\cup B\right)=n\left(A\right)+n\left(B\right)$ ，从而有：
   f n ( A ∪ B ) = n ( A ∪ B ) n = n ( A ) + n ( B ) n = n ( A ) n + n ( B ) n = f n ( A ) + f n ( B ) . \\begin{align*} f_{n}\\left( A \\cup B \\right) = & \\frac{n\\left( A \\cup B \\right)}{n} = \\frac{n\\left( A \\right) + n\\left( B \\right)}{n} \\\\ = & \\frac{n\\left( A \\right)}{n} + \\frac{n\\left( B \\right)}{n} = f_{n}\\left( A \\right)+f_{n}\\left( B \\right). \\end{align*}fn​(A∪B)==​nn(A∪B)​=nn(A)+n(B)​nn(A)​+nn(B)​=fn​(A)+fn​(B).​

1.2.4 确定概率的古典方法

确定概率的古典方法比较简单，主要内容为频率、频数的概念介绍，因此不在这里赘述（直接看书即可）。
接下来在下面记录一些较为有用的模型。

抽样模型（不放回抽样）

• 一批产品共有 $N$ 件，其中 $M$ 件是不合格品，$N-M$ 件是合格品，从中随机取出 $n$ 件 $\left(n⩽N\right)$ ,试求事件 A m = A_{m} = Am​= “取出的 $n$ 件产品中有 $m$ 件不合格品” 的概率，其中 $\left(m⩽M,n-m⩽N-M\right).$

思路：先计算样本空间 $\Omega$ 中样本点的总数：从 $N$ 件产品中任取 $n$ 件，因为不讲次序，所以样本点的总数为 ( N n ) . \\binom{N}{n}. (nN​). 又因为是随机抽取的，所以这 ( N n ) \\binom{N}{n} (nN​) 个样本点是等可能的。在得到样本空间的样本点总数之后，再计算一般发生事件中含有的样本点个数，再去除样本空间的样本点数量，从而得到概率值。

接下来先计算事件 A 0 , A 1 A_{0},A_{1} A0​,A1​的概率，然后再计算 A m A_{m} Am​ 的概率。

A 0 A_{0} A0​

因为事件 A 0 = A_{0} = A0​= “取出的 $n$ 件产品中有 $m$ 件不合格产品” $=$ “取出的 $n$ 件产品全是合格的产品” ，这意味着取出的 $n$ 件产品全是从 $N-M$ 件合格品中抽取，所以有 ( N − M n ) \\binom{N-M}{n} (nN−M​) 种取法，故 A 0 A_{0} A0​ 的概率为：
P ( A 0 ) = ( N − M n ) ( N n ) P \\left( A_{0} \\right) = \\frac{\\binom{N-M}{n}} {\\binom{N}{n}} P(A0​)=(nN​)(nN−M​)​
(注：这是组合公式，因为不讲次序。)

A 1 A_{1} A1​

事件 A 1 = A_{1} = A1​= “取出的 $n$ 件产品中有 $1$ 件不合格产品”，要使取出的 $n$ 件产品中只有 $1$ 件不合格品，其他 $n-1$ 件是合格品，那么必须分两步进行：

1. 从 $M$ 件不合格品中随机取出 $1$ 件，共有 ( M 1 ) \\binom{M}{1} (1M​) 种取法.
2. 从 $N-M$ 件合格品种随机取出 $n-1$ 件，共有 ( N − M n − 1) \\binom{N-M}{n-1} (n−1N−M​) 种取法,

所以根据乘法原理， A 1 A_{1} A1​ 中共有 ( M 1 ) ( N − M n − 1) \\binom{M}{1} \\binom{N-M}{n-1} (1M​)(n−1N−M​) 个样本点.故 A 1 A_{1} A1​ 的概率为：
P ( A 1 ) = ( M 1 ) ( N − M n − 1 ) ( N n ). P \\left( A_{1} \\right) = \\frac{\\binom{M}{1} \\binom{N-M}{n-1}} {\\binom{N}{n}}. P(A1​)=(nN​)(1M​)(n−1N−M​)​.

A m A_{m} Am​

有了以上对 A 0 A_{0} A0​ 和 A 1 A_{1} A1​ 的分析，很容易计算出一般事件 A m A_{m} Am​ 中含有的样本点个数：要使 A m A_{m} Am​ 发生，必须从 $M$ 件不合格品中抽 $m$ 件，再从 $N-M$ 件合格品中抽 $n-m$ 件，根据乘法原理， A m A_{m} Am​ 含有 ( M m ) ( N − M n − m) \\binom{M}{m} \\binom{N-M}{n-m} (mM​)(n−mN−M​) 个样本点，由此得 A m A_{m} Am​ 的概率为：
P ( A m) = ( M m ) ( N − M n − m ) ( N n ) , m = 0 , 1 , 2 , … , r , ( r = m i n { n , M } ) . (1.2.5) \\begin{align} P \\left( A_{m} \\right) = \\frac{\\binom{M}{m} \\binom{N-M}{n-m}} {\\binom{N}{n}}, m = 0,1,2,\\dots,r,(r=min\\left\\{ n,M \\right\\}). \\end{align} \\tag{1.2.5} P(Am​)=(nN​)(mM​)(n−mN−M​)​,m=0,1,2,…,r,(r=min{n,M}).​(1.2.5)
注意：在此应有 $m⩽n,m⩽M,$ 所以 m⩽min { n , M } m \\leqslant min\\left\\{ n, M \\right\\} m⩽min{n,M}。
对于不放回抽样这类问题（例如彩票问题），可以考虑将全部可能性的种类列出来，再一一计算对应的可能情况（利用乘法原理），最后求和。

抽样模型（放回抽样）

• 一批产品共有 $N$ 件，其中 $M$ 件是不合格品，$N-M$ 件是合格品，从中随机取出 $n$ 件 $\left(n⩽N\right)$ ,且取出之后在登记完之后，会将取出的产品放回。试求事件 B m = B_{m} = Bm​= “取出的 $n$ 件产品中有 $m$ 件不合格品” 的概率，其中 $\left(m⩽M,n-m⩽N-M\right).$

思路：先计算样本空间 $\Omega$ 中样本点的总数：从 $N$ 件产品中任取 $1$ 件，因为是放回抽样，且不讲究次序，所以第二次抽取时，任然有 $N$ 种取法，所以共有 N n N^{n} Nn 个等可能的样本点。

接下来先计算事件 B 0 , B 1 B_{0},B_{1} B0​,B1​的概率，然后再计算 B m B_{m} Bm​ 的概率。(事实上，熟悉之后可以直接想到 B m B_{m} Bm​ 的情况应当如何求)。

B 0 B_{0} B0​

事件 B 0 = B_{0} = B0​= “取出的 $n$ 件产品全是合格品” 发生必须从 $N-M$ 件合格品中有放回地抽取 $n$ 次，所以 B 0 B_{0} B0​ 中含有 ( N − M ) n \\left( N-M \\right)^{n} (N−M)n 个样本点，故 B 0 B_{0} B0​ 的概率为：
P ( B 0 ) = ( N − M ) n N n= ( 1 − M N ) n . P\\left( B_{0} \\right) = \\frac{\\left( N-M \\right)^{n}} {N^{n}} = \\left( 1-\\frac{M}{N} \\right)^{n}. P(B0​)=Nn(N−M)n​=(1−NM​)n.

B 1 B_{1} B1​

事件 B 1 = B_{1} = B1​= “取出的 $n$ 件产品中有 $1$ 件不合格产品” 发生必须从 $N-M$ 件合格品中有放回地抽取 $n-1$ 次，从 $M$ 件不合格品中抽取 $1$ 次，这样就有 M⋅ ( N − M )n − 1 M \\cdot \\left( N-M \\right)^{n-1} M⋅(N−M)n−1 种取法。再考虑到这件不合格品可能在第 $1$ 次抽取中得到，也可能在第 $2$ 次抽取中得到，$\cdots \cdots$ 也可能在第 $n$ 次抽取中得到，总共有 $n$ 种可能，所以 B 1 B_{1} B1​ 中含有 n⋅M⋅ ( N − M )n − 1 n \\cdot M \\cdot \\left( N-M \\right)^{n-1} n⋅M⋅(N−M)n−1 个样本点，故 B 1 B_{1} B1​ 的概率为：
P ( B 1 ) = n M ( N − M ) n − 1 N n= n M N ( 1 − M N ) n − 1. P\\left( B_{1} \\right) = \\frac{nM \\left( N-M \\right)^{n-1}} {N^{n}} = n\\frac{M}{N} \\left( 1-\\frac{M}{N} \\right)^{n-1}. P(B1​)=NnnM(N−M)n−1​=nNM​(1−NM​)n−1.

B m B_{m} Bm​

1. 事件 B m = B_{m} = Bm​= “取出的 $n$ 件产品中有 $m$ 件不合格产品” 发生必须从 $N-M$ 件合格品中有放回地抽取 $n-m$ 次，从 $M$ 件不合格品中有放回地抽取 $m$ 次，这样就有 M m ⋅ ( N − M ) n − m M^{m} \\cdot \\left( N-M \\right)^{n-m} Mm⋅(N−M)n−m 种取法。
2. 再考虑到这 $m$ 件不合格品可能在 $n$ 次中的任何 $m$ 次抽取中得到，总共有 ( n m ) \\binom{n}{m} (mn​) 种可能。所以事件 B m B_{m} Bm​ 含有 ( n m )M m ( N − M ) n − m \\binom{n}{m} M^{m} \\left( N-M \\right)^{n-m} (mn​)Mm(N−M)n−m 个样本点，故 B m B_{m} Bm​ 的概率为：
   P ( B m ) = ( n m ) M m ( N − M ) n − m N n = ( n m ) ( M N ) m ( 1 − M N ) n − m , m = 0 , 1 , 2 , ⋯   , n . \\begin{align*} P(B_m) = & \\binom{n}{m} \\frac{M^m (N-M)^{n-m}}{N^n} \\\\ = & \\binom{n}{m} \\left( \\frac{M}{N} \\right)^{m} \\left( 1-\\frac{M}{N} \\right)^{n-m},m=0,1,2,\\cdots,n. \\end{align*}P(Bm​)==​(mn​)NnMm(N−M)n−m​(mn​)(NM​)m(1−NM​)n−m,m=0,1,2,⋯,n.​
   由于是抽样放回，不合格品在整批产品中所占比例 M N \\frac{M}{N} NM​ 是不变的，记此比例为 $p$ ，则上式可以写为：
   P ( B m) = ( n m ) p m ( 1 − p ) n − m , m = 0 , 1 , 2 , ⋯   , n . (1.2.6) \\begin{align} P(B_m) = \\binom{n}{m} p^{m} \\left( 1-p \\right)^{n-m},m=0,1,2,\\cdots,n. \\end{align} \\tag{1.2.6}P(Bm​)=(mn​)pm(1−p)n−m,m=0,1,2,⋯,n.​(1.2.6)
   注：此处有一关联知识点————二项分布。

其余相同重要的模型/问题还有：盒子模型，生日问题（其中，生日问题的近似计算公式是将原式先取对数，然后进行泰勒展开之后再求和得到的）。

1.2.5 确定概率的几何方法

确定概率的几何方法，其基本思想是：

1. 如果一个随机现象的样本空间 $\Omega$ 充满某个区域，其度量（长度、面积或体积等）大小可用 S ΩS_{\\Omega} SΩ​ 表示。

2. 任意一点落在度量相同的子区域内（可能位置不同）是等可能的，譬如在样本空间 $\Omega$ 中有一单位正方形 $A$ 和直角边为 $1$ 与 $2$ 的直角三角形 $B$，而落在点区域 $A$ 和区域 $B$ 是等可能的，因为这两个区域面积相等。（如下图所示）

   

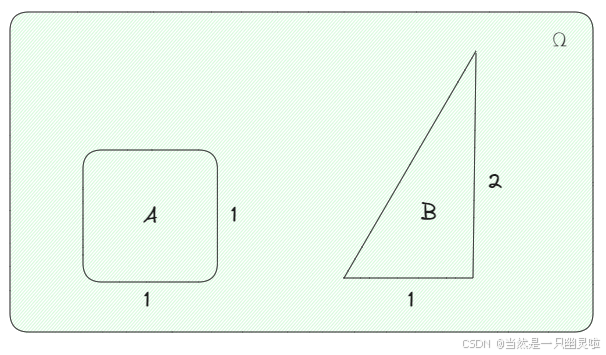
   用大白话来说，就是任意两个“面积（度量）相同的事件”发生概率是一致的。

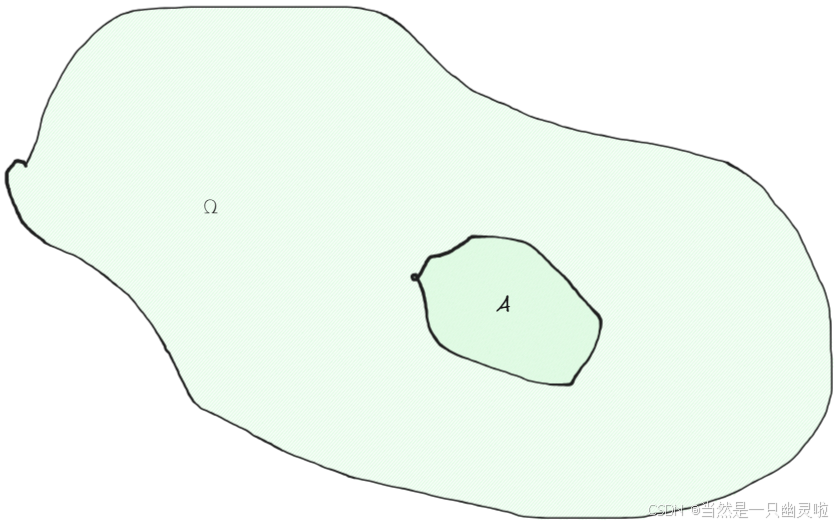
3. 若事件 $A$ 为 $\Omega$ 中的某个子区域（如下图所示），且其度量大小可用 S AS_{A} SA​ 表示，则事件 $A$ 的概率为：
   P ( A ) = S A S Ω (1.2.7) \\begin{align*} P\\left( A \\right) = \\frac{S_{A}}{S_{\\Omega}} \\end{align*} \\tag{1.2.7} P(A)=SΩ​SA​​​(1.2.7)
   这个概率称为几何概率，它满足公理化定义。

求几何概率的关键是对样本空间 $\Omega$ 和所求事件 $A$ 用图形描述清楚（一般用平面或空间图形）。然后计算出相关图形的度量（一般为面积或体积）。
与之相关的一些问题有：会面问题，比丰投针问题（蒙特卡洛法），贝特朗奇论。

1.2.6 确定概率的主观方法

在现实世界里有一些随机事现象是不能重复或者不能大量重复的，这时有关事情的概率如何确定呢？

统计界的贝叶斯学派认为：一个事件的概率是人们根据经验对该事件发生的可能性所给出的个人信念，这样给出的概率成为主观概率。
而主观概率有以下特点（笔者认为，这也是德尔菲法的依据）：

1. 主观概率和主观臆造有着本质上的不同，前者要求当事人对所考察的事件有透彻的了解和丰富的经验，甚至是这一行的专家，并能对历史信息和当时信息进行仔细分析，如此确定的主观概率是可信的。
2. 用主观方法得出的随机事件发生的可能性大小，本质上是对随机事件概率的一种推断和估计。虽然结论的精确性有待实践的检验和修正，但结论的可信性在统计意义上是有其价值的。
3. 在遇到的随机现象无法大量重复时，用主观方法去做决策和判断是适合的。从这点来看，主观方法至少是频率方法的一种补充。

• 主观给定的概率要符合公理化的定义。