leecodehot100刷题--矩阵

73. 矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

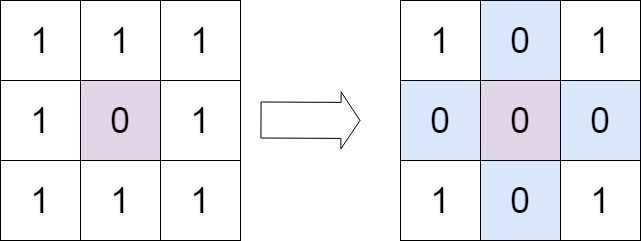
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

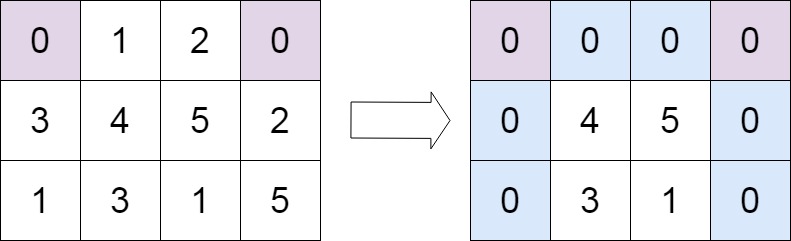
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

这道题的解题思路是：

• 第一次遍历
  逐元素检查矩阵，如果 matrix[i][j] == 0，就将 zero_rows[i] 和 zero_cols[j] 标记为 true。

• 第二次遍历行
  遍历 zero_rows，对于为 true 的行，将该行所有元素设置为 0。

• 第三次遍历列
  遍历 zero_cols，对于为 true 的列，将该列所有元素设置为 0。

class Solution {public: void setZeroes(vector<vector>& matrix) { int row = matrix.size(); int col = matrix[0].size(); vectorvec_row(row,false); vectorvec_col(col,false); for(int i = 0; i<row; i++) { for(int j=0; j<col; j++) { if(matrix[i][j] == 0) { vec_row[i] = true; vec_col[j] = true; } } } for(int i=0; i<row; i++) { if(vec_row[i]==true) { for(int j=0; j<col; j++) { matrix[i][j] = 0; } } } for(int i=0; i<col; i++) { if(vec_col[i]==true) { for(int j=0; j<row; j++) { matrix[j][i] = 0; } } } }};

54. 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

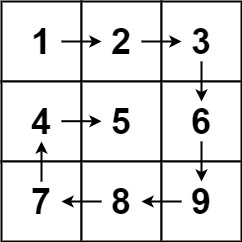
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

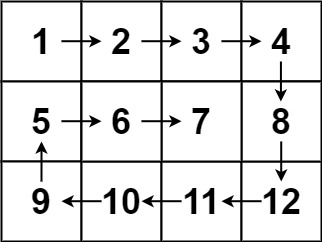
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

这里的解题思路是：

定义四个边界指针：top、bottom、left、right用来界定指针移动的范围，不断地将指针从左到右移动->从上到下移动->从右到左移动->从下到上这样循环移动。最后保证while(top<=bottom&&left<=right),这样可以防止四个边界值出现越界的情况。

class Solution {public: vector spiralOrder(vector<vector>& matrix) { vector result; int top = 0; int left = 0; int bottom = matrix.size()-1; int right = matrix[0].size()-1; while(left<=right && top<=bottom) { for(int col=left; col<=right; col++) { result.push_back(matrix[top][col]); } top++; for(int row=top; row<=bottom; row++) { result.push_back(matrix[row][right]); } right--; if (top =left; col--) { result.push_back(matrix[bottom][col]); } bottom--; } if(left =top; row--) { result.push_back(matrix[row][left]); } left++; } } return result; }};

48. 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

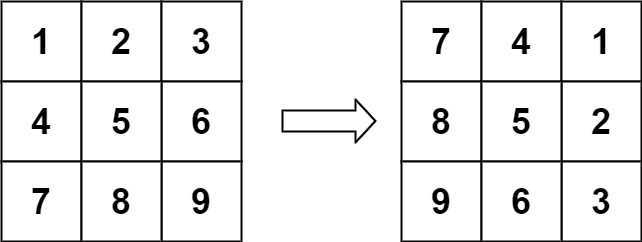
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

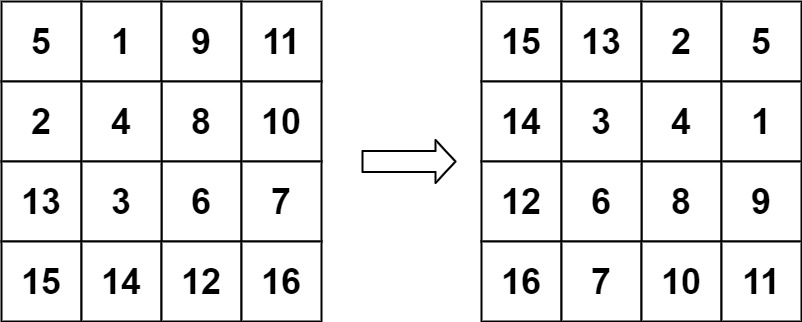
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

 这道题的做法是：

1、先将整个矩阵沿主对角线转置矩阵

2、左右翻转每一行元素

class Solution {public: void rotate(vector<vector>& matrix) { int n = matrix.size(); for(int i = 0; i < n; i++) { for(int j = 0; j<i; j++) { swap(matrix[i][j], matrix[j][i]); } } for(int i = 0; i < n; i++) { for(int j=0; j < n/2; j++) { swap(matrix[i][j], matrix[i][n-1-j]); } } }};

240. 搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

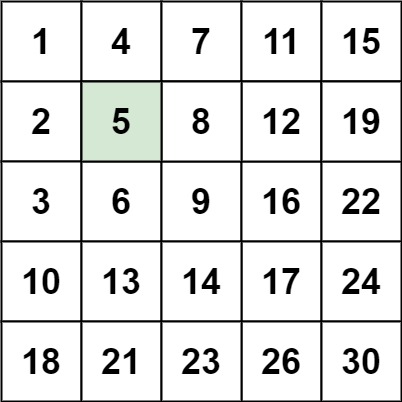
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5输出：true

示例 2：

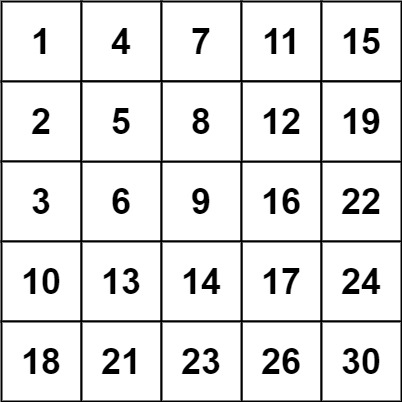
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20输出：false

这道题的思路是：

我们利用两个指针：行指针和列指针，从最右边列的元素与target元素进行比较：

如果target == x，那么就返回true；

如果target > x，说明x还是太小了，但是x是这一行最大的元素，就往下一行找；

如果target < x,   那么说明x比较大，则往x这一行的左边寻找，若target与x这一行一直左移后的元素不等，如果出现左移的元素<target,那么往下一行寻找。

class Solution {public: bool searchMatrix(vector<vector>& matrix, int target) { int m = matrix.size(); int n = matrix[0].size(); int i = 0; int j = n-1; while (i = 0) { if(matrix[i][j] == target) { return true; }else if(matrix[i][j] > target) { j--; }else if(matrix[i][j] < target) { i++; } } return false; }};