你再也找不到更详细的3DGS教程了 —— 一万九千字长文解析3DGS_3dgs 透视投影

技术文档

参考：

https://www.bilibili.com/video/BV1MF4m1V7e3/

https://blog.csdn.net/2401_86810419/article/details/148811121

https://www.bilibili.com/video/BV1cz421872F?t=233.9

https://wuli.wiki/online/SphHar.html

https://zhuanlan.zhihu.com/p/467466131

特别指出的是SY__007的3DGS较真系列，对本文有极大的启发和参考价值，下文有很多截图也直接来自视频，强烈推荐大家移步小破站，去观看视频。

做雪球?

What is splatting？

关于Splat，在英语中作抛雪球打击到墙面的拟声词。

Splatting是一种体渲染的方法：将3D物体渲染到2D平面

与NeRF中的渲染方法的差异：

NeRF中使用Ray-casting（类似射线求积分）：是计算像素点收到发光粒子的影响来生成图像。

3DGS中使用Splatting这种主动的方法，计算发光粒子如何影响像素点

Splatting算法的核心：

1.选择雪球

2.抛掷雪球：从3D投影到2D，得到足迹（footprint）

3.加以合成，得到最终的图像

一：为什么使用核（雪球，Gaussian）：

基于Gaussian的数学性质：

1.Gaussian本身是闭合的椭球，经过仿射变换后依旧是封闭的

2.高维Gaussian降维（沿某个轴进行积分）之后依旧是Gaussian

对于椭球Gaussian：

其中x是三维空间中的点，

μ是高斯分布的均值向量，表示Gaussian的中心点位置

Σ是协方差矩阵，描述Gaussian在3D空间中的形状和方向，它是半正定的

为什么这是一个椭球？

首先去了解协方差矩阵。

对于Gauss分布：

一维：形状由均值&方差决定

高维：形状由均值&协方差矩阵决定

对于协方差矩阵：

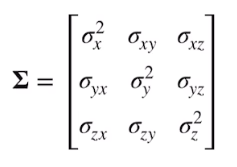
是一个对称矩阵，决定高斯分布形状
对角线上元素为x轴/y轴/z轴的方差
反斜对角线上的值为协方差，表示x和y，x和z........的线性相关程度

这里直接用SY__007写的：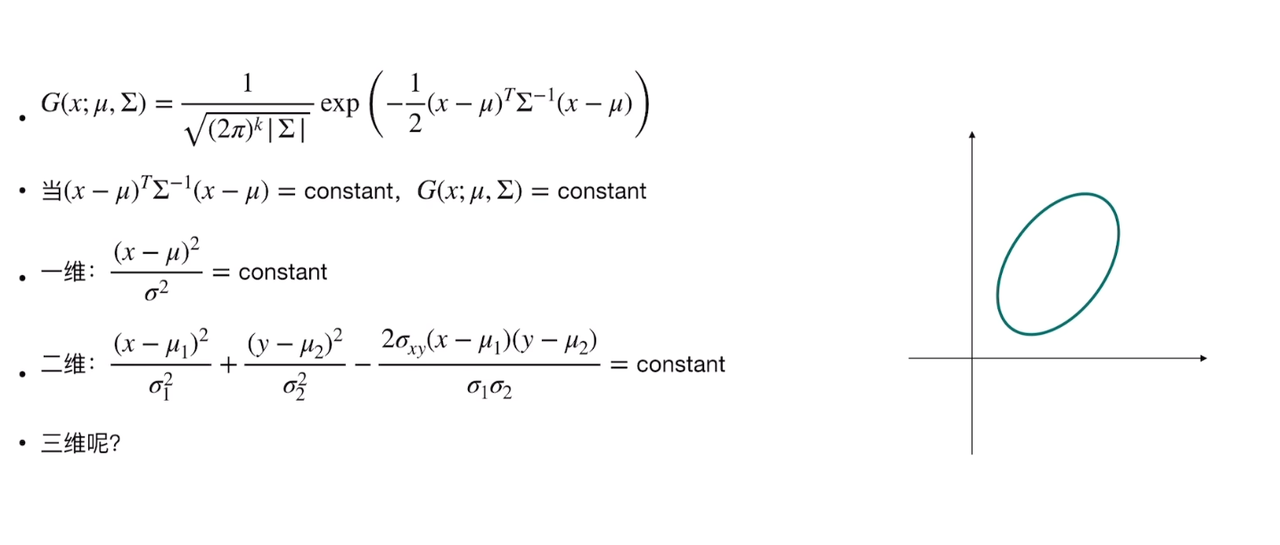

抛雪球

如何进行参数变换？

从3D->像素的过程：

观测变换

观测变换：从世界坐标系-->相机坐标系

投影变换

投影变换：正交投影、透视投影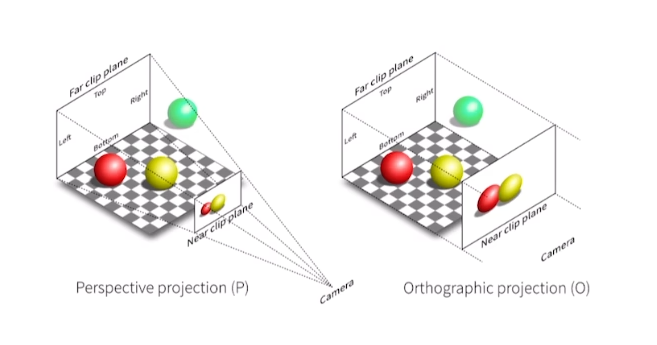

正交投影：

对于立方体[l,r]*[b,t]*[f,n]

1.平移到原点

2.立方体缩放至[-1,1]^3的正方体空间内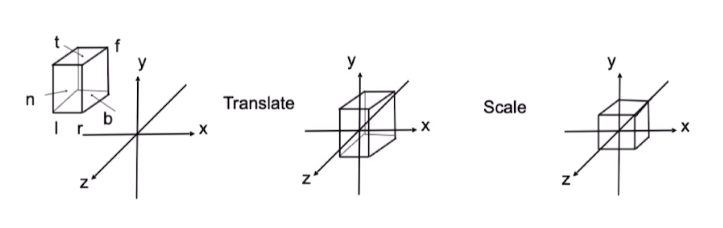

总的来说就是进行了仿射变换，

如题所给的例子的仿射变换即是：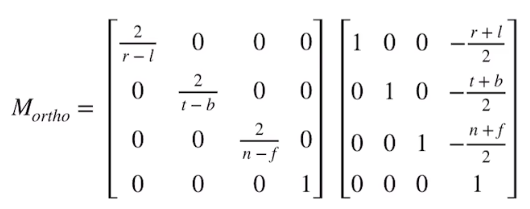

$M_{ortho}=AB$

A这里是缩放矩阵

B为平移矩阵

在正交投影中，我们没有考虑对于原本的长方体的长和宽的比例不同，导致的缩放比例不同，其实产生了畸变，这个问题会在之后的视口变换解决

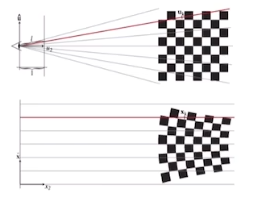
透视投影：

透视投影需要满足近大远小的条件

对于视锥，我们先把他变换为‘立方体’，再进行正交投影

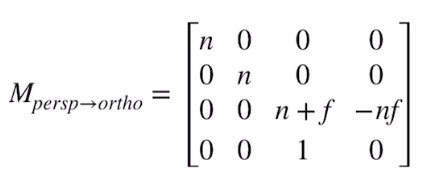
数学过程实在懒得写了，这里直接放上作者手稿一张

问题？：

透视投影是非线性的，也就是非放射变换，但是高斯椭球经过仿射变换后是高斯，但非仿射变换就不一定。

视口变换：

我们从简化的图形渲染管线开始：

3D 顶点 → 模型变换 → 视图变换 → 投影变换 → 裁剪 → 标准化设备坐标 → 视口变换 → 屏幕像素

之前的变换已经将顶点从”模型局部坐标“转换成NDC空间坐标，以OpenGL为例，正交投影下为[-1,1]×[-1,1]×[-1,1]

视口变换的目的就是把可见区域的标准化坐标，映射到显示器的实际像素区域，让图形真正显示在屏幕上。

视口变换的数学实现

核心是缩放+平移的组合，把NDC范围映射到屏幕视口的像素范围：

(1)以OpenGL经典的[-1.1]立方体为例（xy对应屏幕二维，z用于深度缓冲）：

NDC的x范围: $x_{ndc}\\in [-1,1]$
NDC的y范围： $y_{ndc}\\in [-1,1]$
NDC的z范围： $z_{ndc}\\in [-1,1]$ (或者[0,1],这取决于深度缓冲装置)

(2)目标视口的像素范围

假设屏幕视口的：

左下角像素坐标：（x0,y0）（比如窗口内视口偏移，或全屏时 (0,0)）
宽度：width（像素数，如 800 ）、高度：height（像素数，如 600 ）
深度范围（可选，用于深度缓冲）：[zNear,zFar]（比如 [0,255] 或浮点深度）

(3)视口变换矩阵与公式

视口变换通过缩放矩阵+平移矩阵,实现对标准化坐标 $(x_{ndc},y_{ndc},z_{ndc})$ ,变换后得到屏幕像素坐标 $(x_{vp},y_{vp},z_{vp})$

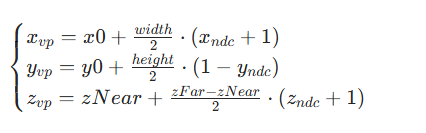
用矩阵形式（齐次坐标下）可以表示为：

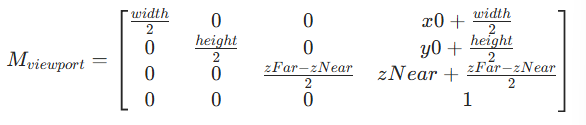
对于 $M_{viewport}$ 进行拆解

1.缩放部分：

x方向： $\\frac{width}{2}$ 把[-1,1]缩放为[0,width]范围；
y方向： $\\frac{height}{2}$ 把[-1,1]缩放为[0,height]范围，但考虑到屏幕坐标系一般y轴\"向下为上”（与NDC相反），所以使用 $(1-y_{ndc})$ 反转；
z方向： $\\frac{zFar-zNear}{2}$ 把[-1,1]缩放为[zNear,zFar]（深度缓冲的实际范围）

2.平移部分

x 平移 $x0+\\frac{width}{2}$ ，让缩放后的 [0,width] 起点对齐视口左下角 x0；
y 平移 $y0+\\frac{height}{2}$ ，同理对齐视口左下角 y0；
z 平移 $zNear + \\frac{zFar - zNear}{2}$ ，让缩放后的深度对齐 zNear 起点。

视口变换的实际作用：

从虚拟坐标到物理屏幕
支持多视角渲染
深度缓冲的落地

光栅化：

1.光栅化的位置：渲染管线‘矢量-->像素’转换

简单渲染管线流程为：

3D 顶点 → 变换（模型/视图/投影）→ 裁剪 → 标准化设备坐标（NDC）→ 光栅化 → 像素着色 → 帧缓冲 → 屏幕

前面的变换，把顶点转成抽象的数学坐标（如NDC空间下的[-1,1]立方体）
光栅化要解决：如何把这些矢量图元拆解成屏幕上的离散像素，让每个像素知道“属于哪个图元，该染什么颜色”

2.光栅化的核心任务:图元的“离散化”

（1）输入：图元的“数学描述”

以三角形为例（图形学的最基础图元，复杂模型由三角形拼接），输入是三个顶点的坐标（NDC或视口变换后的屏幕坐标），以及顶点附带的属性（颜色、法向量、纹理坐标等）。

（2）输出：像素的“归属与属性”

输出是覆盖这些三角形的所有像素，并为每个像素插值计算属性（比如/顶点颜色查指出像素颜色，纹理坐标插值出采样位置），供后续像素着色器处理。

3.光栅化的关键步骤

（1）三角形 setup（配置）

计算三角形的边方程和包围盒

先找出三角形在屏幕上的最小包围矩形（AABB）,只遍历这个范围内的像素，减少计算量；
推导三角形三条边的数学方程（如ax+by+c=0）,用于判断i像素是否在三角形内

（2）三角形traversal(遍历)

对包围盒捏的每个像素（或\'采样点\'），用便方程判断是否在三角形内（比如OpenGL的“winding order”规则，或计算重心坐标）。
若像素在三角形内，就标记为属于该三角形，并进入属性插值阶段

（3）属性插值

三角形三个顶点有属性（如颜色 $C_0,C_1,C_2$ 、纹理坐标 ${uv}_0,uv_1,uv_2$ ），用重心坐标对像素属性做线性插值：

假设像素重心坐标为（α，β，γ）（满足 $\\alpha+\\beta+\\gamma=1$ ）

这里的α，β，γ和数学上的不一样：

假设三角形的三个顶点的坐标分别为：

$(x_1,y_1),(x_2,y_2),(x_3,y_3)$

那么三角形内部的任意一点P(x,y)可以表示为

$P(x,y)=\\alpha(x_1,y_1)+\\beta(x_2,y_2)+\\gamma(x_3,y_3)$

那么当满足 $\\alpha+\\beta+\\gamma=1$ 时，P即为三角形重心

则像素颜色 ${C}=\\alpha{C_0}+\\beta{C_1}+\\gamma{C_2}$

纹理坐标同理

以下是AABB的方法示例：

import numpy as npclass AABB: \"\"\"轴对齐包围盒(AABB)类，用于3D高斯溅射场景中的空间管理\"\"\" def __init__(self): \"\"\"初始化AABB，设置初始边界为无穷大\"\"\" self.min = np.array([np.inf, np.inf, np.inf], dtype=np.float32) # 最小点 self.max = np.array([-np.inf, -np.inf, -np.inf], dtype=np.float32) # 最大点 def expand_by_point(self, point): \"\"\"通过点扩展AABB边界 Args: point: 3D坐标点，形状为(3,)的numpy数组 \"\"\" self.min = np.minimum(self.min, point) self.max = np.maximum(self.max, point) def expand_by_gaussian(self, mean, scale): \"\"\"通过高斯分布扩展AABB边界，考虑高斯的尺度 Args: mean: 高斯分布的均值，形状为(3,)的numpy数组 scale: 高斯分布的尺度参数，形状为(3,)的numpy数组 \"\"\" # 对于3DGS，通常使用3倍标准差作为边界（覆盖大部分分布） self.expand_by_point(mean - 3 * scale) self.expand_by_point(mean + 3 * scale) def expand_by_aabb(self, other_aabb): \"\"\"通过另一个AABB扩展当前AABB Args: other_aabb: 另一个AABB实例 \"\"\" self.min = np.minimum(self.min, other_aabb.min) self.max = np.maximum(self.max, other_aabb.max) def contains_point(self, point): \"\"\"判断点是否在AABB内部 Args: point: 3D坐标点，形状为(3,)的numpy数组  Returns: bool: 点是否在AABB内 \"\"\" return np.all((point >= self.min) & (point <= self.max)) def intersects_aabb(self, other_aabb): \"\"\"判断与另一个AABB是否相交 Args: other_aabb: 另一个AABB实例  Returns: bool: 两个AABB是否相交 \"\"\" # 检查每个轴是否不重叠 if (self.max[0]  other_aabb.max[0] or self.max[1]  other_aabb.max[1] or self.max[2]  other_aabb.max[2]): return False return True def get_center(self): \"\"\"计算AABB的中心坐标 Returns: numpy数组: AABB中心的3D坐标 \"\"\" return (self.min + self.max) / 2.0 def get_extents(self): \"\"\"计算AABB在各轴上的延伸范围（半边长） Returns: numpy数组: 各轴方向的半边长 \"\"\" return (self.max - self.min) / 2.0 def get_size(self): \"\"\"计算AABB在各轴上的大小 Returns: numpy数组: 各轴方向的长度 \"\"\" return self.max - self.min def split(self, axis, position): \"\"\"沿指定轴和位置分割AABB为两个子AABB Args: axis: 分割轴，0=x, 1=y, 2=z position: 分割位置  Returns: tuple: 两个子AABB实例 \"\"\" left = AABB() left.min = self.min.copy() left.max = self.max.copy() left.max[axis] = position right = AABB() right.min = self.min.copy() right.min[axis] = position right.max = self.max.copy() return left, right def __str__(self): return f\"AABB(min: {self.min}, max: {self.max})\"# 3DGS中AABB的典型应用示例def example_usage(): # 创建一个AABB用于包含多个高斯 gaussian_means = np.array([ [0.1, 0.2, 0.3], [1.5, 2.0, 1.8], [-0.5, -1.0, 0.2] ]) gaussian_scales = np.array([ [0.1, 0.2, 0.15], [0.3, 0.25, 0.4], [0.2, 0.3, 0.25] ]) # 构建包含所有高斯的AABB global_aabb = AABB() for mean, scale in zip(gaussian_means, gaussian_scales): global_aabb.expand_by_gaussian(mean, scale) print(\"全局AABB:\", global_aabb) print(\"AABB中心:\", global_aabb.get_center()) print(\"AABB大小:\", global_aabb.get_size()) # 测试点是否在AABB内 test_point = np.array([0.0, 0.0, 0.0]) print(f\"点 {test_point} 是否在AABB内: {global_aabb.contains_point(test_point)}\") # 创建一个新的AABB并测试相交 another_aabb = AABB() another_aabb.expand_by_point(np.array([1.0, 1.0, 1.0])) another_aabb.expand_by_point(np.array([2.0, 3.0, 2.0])) print(\"另一个AABB:\", another_aabb) print(\"两个AABB是否相交:\", global_aabb.intersects_aabb(another_aabb))if __name__ == \"__main__\": example_usage()

整体示例代码：

frame = create_canvas(700, 700)angle = 0eye = [0, 0, 5]pts = [[2, 0, -2], [0, 2, -2], [-2, 0, -2]]viewport = get_viewport_matrix(700, 700)# get mvp matrixmvp = get_model_matrix(angle)mvp = np.dot(get_view_matrix(eye), mvp)mvp = np.dot(get_proj_matrix(45, 1, 0.1, 50), mvp) # 4x4# loop pointspts_2d = []for p in pts: p = np.array(p + [1]) # 3x1 -> 4x1 p = np.dot(mvp, p) print(p) p /= p[3] # viewport p = np.dot(viewport, p)[:2] pts_2d.append([int(p[0]), int(p[1])])

3dgs中的观测变换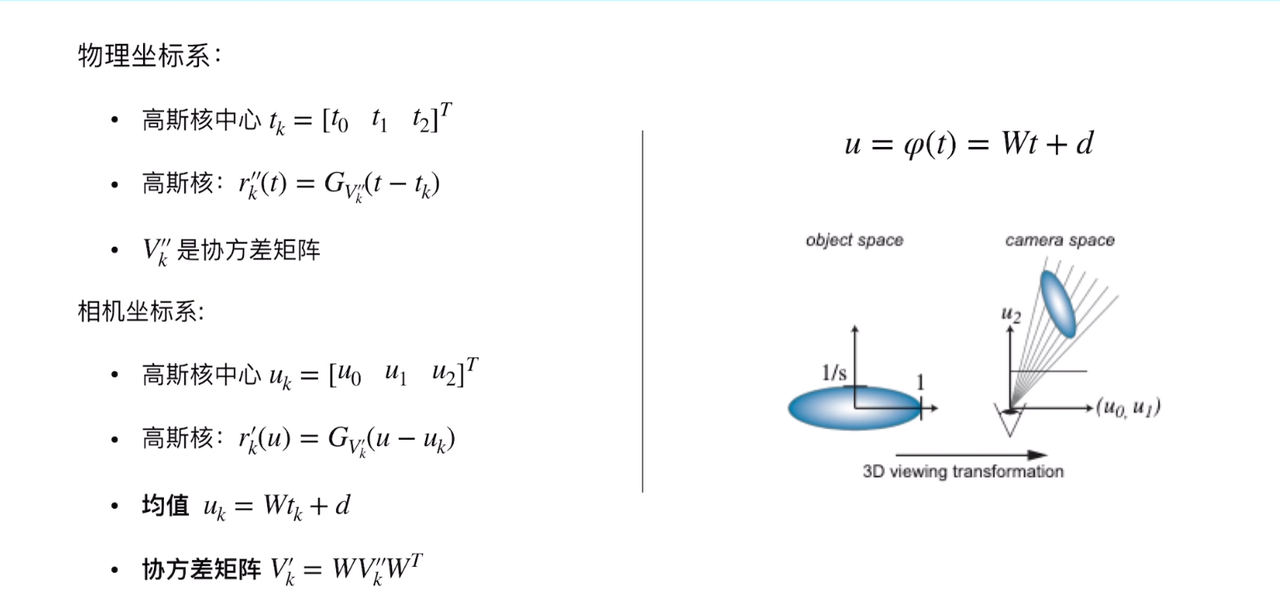

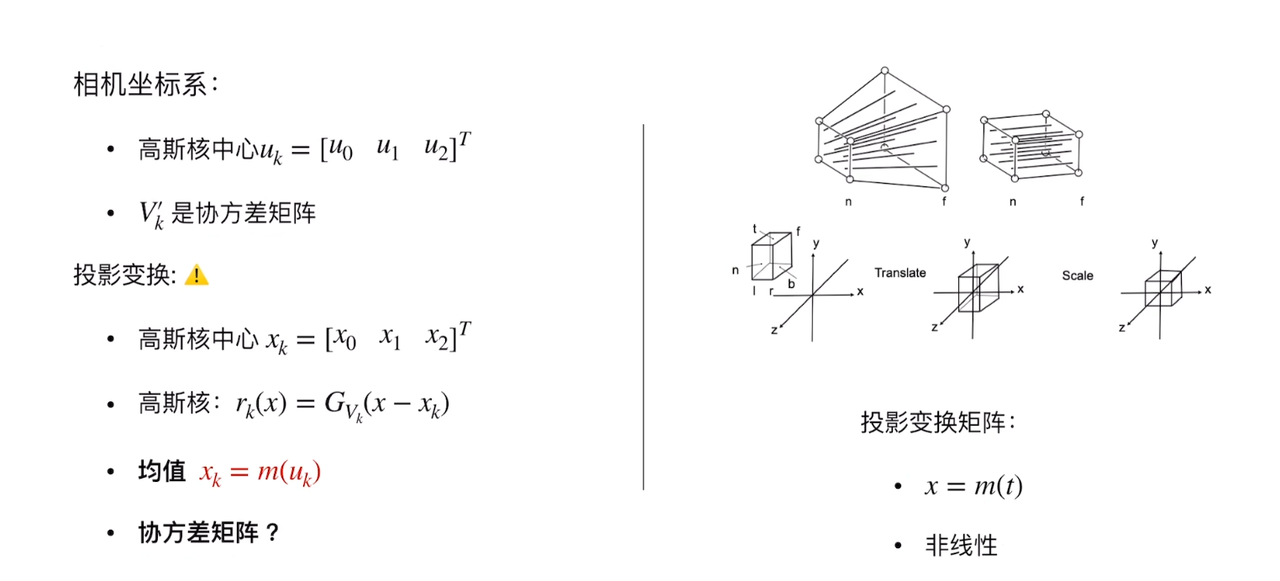
这时候会出现一个问题，对于空间中的点来说进行x=m(t)，这样一个非线性的操作

对于协方差矩阵这样的一个Gaussian做非线性操作，无法得到一个正确的Gaussian

所以在3DGS中引入了Jacobian近似矩阵

对于雅可比矩阵，这里加一些关于数学的理解：

关键词：泰勒展开、偏导数、线性逼近

我们以 $f_1(x)=x+sin(y)$ 和 $f_2(y)=y+sin(x)$ 为例

这里会得到雅可比矩阵：

$J = \\begin{bmatrix} \\frac{\\partial f_1}{\\partial x} & \\frac{\\partial f_1}{\\partial y} \\\\ \\frac{\\partial f_2}{\\partial x} & \\frac{\\partial f_2}{\\partial y} \\end{bmatrix} = \\begin{bmatrix} 1 & \\cos(y) \\\\ \\cos(x) & 1 \\end{bmatrix}$

这是雅可比矩阵的数学计算方式

那么为什么在3DGS中的是一个雅可比近似矩阵呢？

其实是一个概念，更多的是考虑到了雅可比矩阵使用线性来代替局部非线性的思想，所以叫做近似矩阵。

这里使用雅可比矩阵作为变换矩阵

雅可比矩阵怎么求？

我们将透视投影中的例子延续下来：

我们已经得到NDC空间下的一个点 $P_{1}$ ( $\\frac{nx}{z}$ , $\\frac{ny}{z}$ , $(n+f)-\\frac{nf}{z}$ )

根据原本的点 $P(x,y,z)$ ,我们显然可以得到

$f_1(x)=\\frac{nx}{z}$

$f_2(y)=\\frac{ny}{z}$

$f_3(z)=(n+f)-\\frac{nf}{z}$

这样我们就得到了对应的函数，也就自然而然可以得到雅可比矩阵

$J = \\begin{bmatrix} \\frac{df_1}{dx} & \\frac{df_1}{dy} & \\frac{df_1}{dz} \\\\ \\frac{df_2}{dx} & \\frac{df_2}{dy} & \\frac{df_2}{dz} \\\\ \\frac{df_3}{dx} & \\frac{df_3}{dy} & \\frac{df_3}{dz} \\end{bmatrix} = \\begin{bmatrix} \\frac{n}{z} & 0 & -\\frac{nx}{z^2} \\\\ 0 & \\frac{n}{z} & -\\frac{ny}{z^2} \\\\ 0 & 0 & \\frac{nf}{z^2} \\end{bmatrix}$

这样我们完成了近似的操作，但是此时均值和协方差在一个坐标系里么？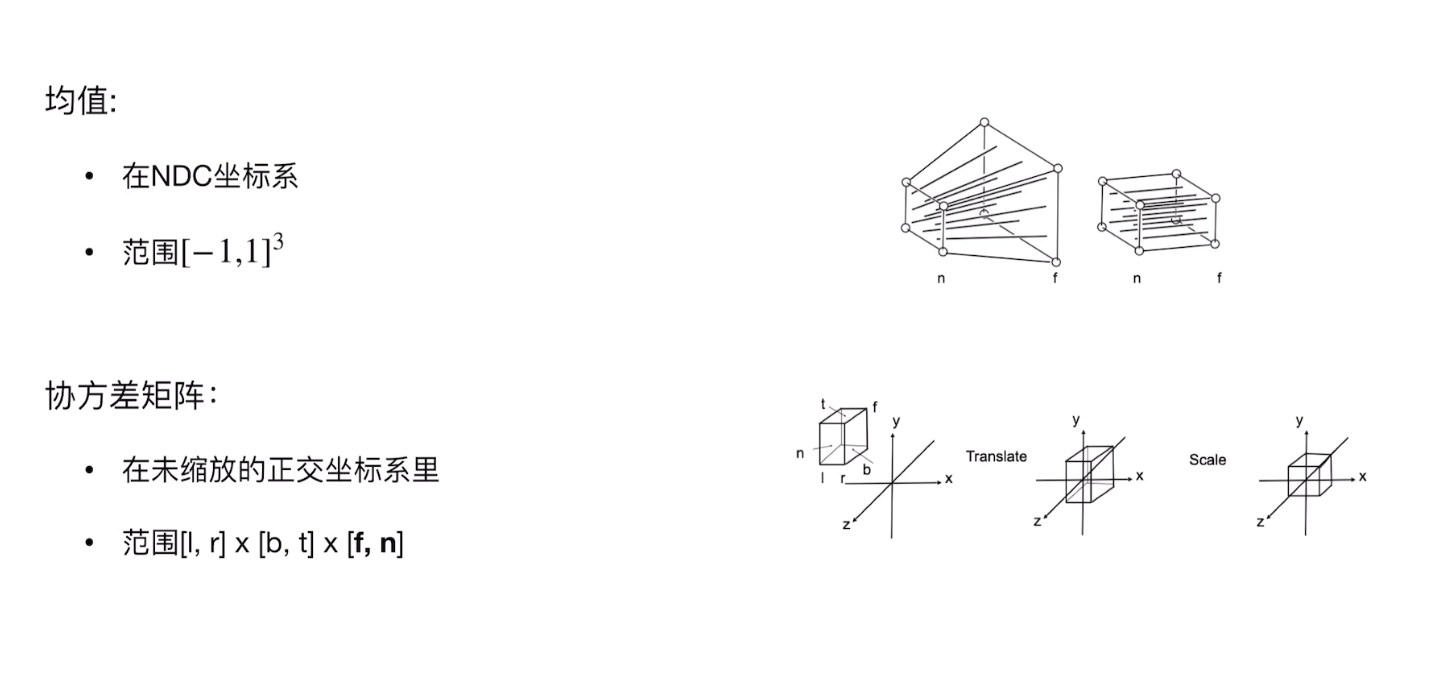

目前为止，对于协方差矩阵，我们只进行了视锥到立方体到正方体的操作，

这是一个未缩放的正交坐标系，和均值所在的NDC坐标系不是一个空间。

所以最后均值需要做视口变换，而协方差矩阵不需要做视口变换

所以在完成以上步骤之后，

我们对高斯核中心 $\\mu=[\\mu_1,\\mu_2,\\mu_3]^T$ 进行平移+缩放即可

而对于协方差矩阵则进行足迹渲染

接下来我们来说足迹渲染

足迹渲染（footprint）？

在3DGS中，足迹渲染是将3D高斯投影到2D平面并生成最终图像的关键过程，类似于将雪球抛向墙面留下扩散痕迹，这些痕迹叠加构成最终图像。而叠加构成就是足迹渲染在做的事情。

什么是footprint？

一句话来说：footprint就是这个高斯在图像平面上投影形成的二维椭圆模糊区域。

Footprint渲染流程

1.高斯体素的投影

3DGS首先将每个高斯 g=（μ，Σ）通过相机外参和内参变换，从世界坐标系变换到了相机坐标系，然后投影到图像平面。

过程如下：

使用线性相机模型投影中心 μ 到图像上的一个像素位置 u
同时，根据协方差Σ与投影变换J计算该高斯在图像上的2D协方差矩阵 $\\sum _{2D}$ ,决定它形成的椭圆大小与方向： $\\sum _{2D}=J\\sum J^T$ 其中J是从3D到2D投影的雅可比矩阵。具体计算方式在上文已经写过。

2.按屏幕空间进行排序(Z-buffer Trick)

渲染顺序要根据深度来决定遮挡关系。3DGS使用前向渲染+屏幕空间Z排序：

按高斯中心深度z对高斯排序
深度近的高斯先渲染，远的后渲染

3.渲染：Rasterization by Splatting

每个高斯体素被当作一个椭圆形纹理，在其图像空间的投影u处进行模糊渲染(splat)，具体过程如下：

对于每个像素(i,j)，判断它是否落在高斯的足迹范围内（比如3σ的椭圆内部）。

若是，使用 $weight=e^{-\\frac{1}{2}(x-\\mu)^T\\sum _{2D}^{-1}(x-\\mu)}$ 来贡献颜色和不透明度。

该公式是二维高斯的密度概率函数，用于像素进行加权模糊。
颜色累计采取 Alpha blending，即 $\\text{C}_{\\text{out}} = \\alpha \\cdot c + (1 - \\alpha) \\cdot \\text{C}_{\\text{prev}}$

4.足迹渲染的优势

避免显示表面建模
高效
连续性好
可微

5.可微性分析

我们采取footprint的策略，保证了渲染管线整体过程的可微分，便于计算梯度与反向传播

雪球颜色：

球谐函数的应用

在3DGS中，球谐函数用于表达颜色。

点云颜色（r,g,b）使用球谐函数来表达，r,g,b均用相同的基球谐函数来表达，

对于每个通道，每个基球谐函数的系数不一样。

这使得点云在不同角度展现出不同的颜色，并有利于提高迭代效率（代码中采用到3阶球谐函数（0，1，2，3），参数量为 $n^2$ 即3*（1+3+5+7）=3*16=48）

球谐函数在一定程度上可以弱化高频信息，达到平滑的目的，但是本质上来说是一种有损压缩，并且能将离散的信息变为连续信息，可计算梯度并进行迭代

从具体代码上来看：

球谐系数已经被直接给出，如下

SH_C0 = 0.28209479177387814SH_C1 = 0.4886025119092199SH_C2 = [1.0925484305920792, -1.0925484305920792, 0.31539156525252005, -1.0925484305920792, 0.5462742152960396]SH_C3 = [-0.5900435899266435, 2.890611442640554, -0.4570457994644658, 0.330763352901154, -0.4570457994644658, 1.443505721320277, -0.5900435899266435]

具体的计算在computeColorFromSH中

def computeColorFromSH(deg, pos, campos, sh): \"\"\" Args： deg:用到球谐函数的阶数，在这里前面已经定义过为3 pos：3D Gaussian的中心位置 campos：相机位置 sh:之前已经定义过的SH系数 \"\"\" dir = pos - campos dir = dir / np.linalg.norm(dir) result = SH_C0 * sh[0] if deg > 0: x, y, z = dir result = result - SH_C1 * y * sh[1] + SH_C1 * z * sh[2] - SH_C1 * x * sh[3] if deg > 1: xx = x * x yy = y * y zz = z * z xy = x * y yz = y * z xz = x * z result = (result + SH_C2[0] * xy * sh[4] + SH_C2[1] * yz * sh[5] + SH_C2[2] * (2.0 * zz - xx - yy) * sh[6] + SH_C2[3] * xz * sh[7] + SH_C2[4] * (xx - yy) * sh[8])return result

这样我们完成了关于颜色的计算

为什么球谐函数可以更好的表达颜色？

从直观上来讲，传统的[R,G,B]使用3个参数，而SH则使用了48个参数来表达，实现了颜色的更精细的控制。

在CG的环境贴图中，经常会使用到球形环境贴图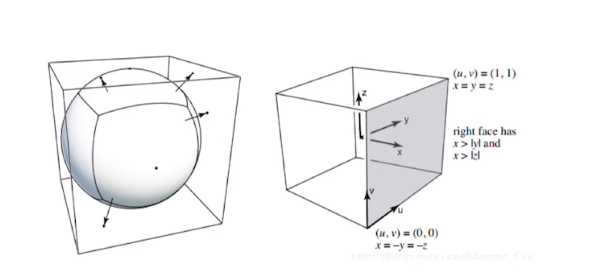

在渲染当中，我们常常使用球谐函数来重建亮度，采用1阶到6阶的球谐函数，当球谐函数的阶数越高，还原的效果越好，同时人的视觉感觉也就越好。

更数学一点来说，

得益于SH的源头勒让德多项式的正交性，球谐函数也是正交的，能够对球面上的信号进行极其高效的编码。
得益于球谐函数的组合性，我们可以根据场景需求，将低阶的球谐函数用于描述全局的、平滑的光照效果，而高阶球谐函数用于捕捉局部的、细节丰富的光照变化
球谐函数也拥有优良的旋转不变性，对于运动的物体或者运动的观测来说，非常有帮助
对于点云，球谐函数对颜色信息实现了有效的压缩存储，比起存储复杂的每个方向的颜色值，只是用了少量的参数来近似复杂的颜色分布

合成图片

直观上：

进行α-blending

sheets=[]#这里存储了所有的高斯 for g in gaussians: sheets.append(g.footprint) alpha_blending(sheets)

实际的代码中：

G.printfoot，依然对每个像素进行着色

import numpy as npdef project_gaussian_to_image(gaussian, camera): \"\"\"将3D高斯投影到图像平面，计算其2D足迹参数\"\"\" # 3D高斯中心投影到图像平面 xyz = gaussian[\'xyz\'] uv = camera.project(xyz) # 得到图像平面上的坐标 # 计算协方差矩阵的投影 cov3d = gaussian[\'cov3d\'] # 3D协方差矩阵 R = camera.rotation_matrix # 相机旋转矩阵 K = camera.intrinsic_matrix # 相机内参矩阵 # 将3D协方差转换到相机坐标系 cov_cam = R @ cov3d @ R.T # 透视投影对协方差的影响 # 简化处理：仅考虑缩放和旋转 z = cov_cam[2, 2] # z坐标 cov_2d = (K[:2, :2] @ cov_cam[:2, :2] @ K[:2, :2].T) / (z ** 2) # 计算椭圆参数：主轴、副轴长度和旋转角度 eigenvalues, eigenvectors = np.linalg.eigh(cov_2d) major_axis = np.sqrt(eigenvalues[1]) minor_axis = np.sqrt(eigenvalues[0]) angle = np.arctan2(eigenvectors[1, 1], eigenvectors[0, 1]) return { \'uv\': uv, \'major_axis\': major_axis, \'minor_axis\': minor_axis, \'angle\': angle, \'color\': gaussian[\'color\'] }def render_footprint(footprint, image): \"\"\"将足迹渲染到图像上\"\"\" u, v = footprint[\'uv\'] major = footprint[\'major_axis\'] minor = footprint[\'minor_axis\'] angle = footprint[\'angle\'] color = footprint[\'color\'] # 计算椭圆覆盖的像素范围 # 这里简化处理，实际实现需要更精确的计算 radius = max(major, minor) * 3 # 扩展范围以确保覆盖整个高斯 x_min = max(0, int(u - radius)) x_max = min(image.shape[1], int(u + radius)) y_min = max(0, int(v - radius)) y_max = min(image.shape[0], int(v + radius)) # 对每个像素计算高斯权重并累积颜色 for y in range(y_min, y_max): for x in range(x_min, x_max): # 计算像素到椭圆中心的相对位置 dx = x - u dy = y - v # 旋转坐标以考虑椭圆角度 cos_a = np.cos(angle) sin_a = np.sin(angle) x_rot = dx * cos_a + dy * sin_a y_rot = -dx * sin_a + dy * cos_a # 计算高斯权重 weight = np.exp(-0.5 * ( (x_rot / major) ** 2 +  (y_rot / minor) ** 2 )) / (2 * np.pi * major * minor) # 累积颜色（考虑alpha混合） image[y, x] = (1 - weight) * image[y, x] + weight * color

像素的颜色

采用类似NeRF的方式，我们去求解每个像素的颜色，公式如下

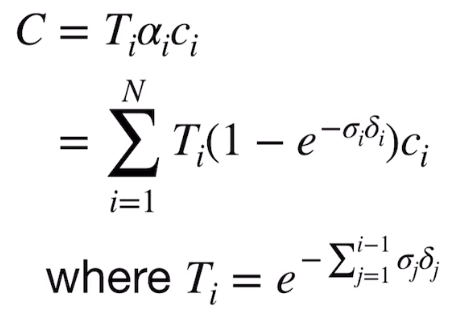
其中的参数：

T（s）,在s点之前，高斯投影没有被阻碍的概率
σ（s）,在s点处，高斯投影阻碍的概率密度
C（s）,在s点处，高斯光出的颜色：

特别的：

Splatting没有找粒子的过程（因为所有的Gauss球都是显示存储的）
需要对高斯球按照深度z排序（Z-buffer Trick），按照从远到近的顺序去进行footprint

关于T（s）,其核心思想为距离相机越近的高斯，对像素的遮挡概率越高，远处高斯的可见性则取决于前方是否有更近的高斯。

具体公式有 $T(s) = \\prod_{s\' \\in S_{closer}} (1 - \\alpha(s\', s))$ 或 $T(i)=e^{-\\sum _{j=1}^{i-1}\\sigma _j\\delta _j}$

二者在弱遮挡的条件下是完全等价的，但仍然常用第二个公式

这里就需要回顾一下NeRF中相关的体渲染相关的知识：

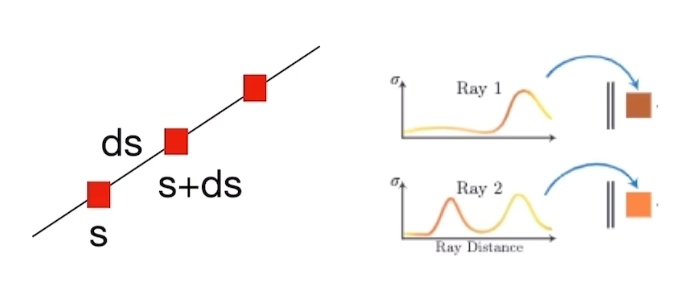
如何将光线上粒子颜色进行求和？

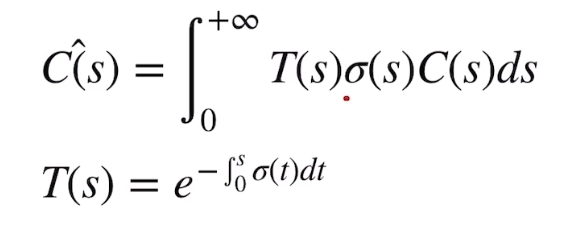
同样的，其中的参数：

T（s）,在s点之前，光线没有被阻碍的概率
σ（s）,在s点处，光线碰击粒子（光线被粒子阻碍）的概率密度
C（s）,在s点处，粒子光出的颜色

各点的颜色和概率密度已知，先求T（s）

经过高斯的遍历，我们就可以得到合成的图片

3DGS为什么快？

事实上，3DGS初始化完全依赖于COLMAP的点云图，与NeRF的粒子数本身并无二致，所以实际上，快的原因为GPU运算的优化

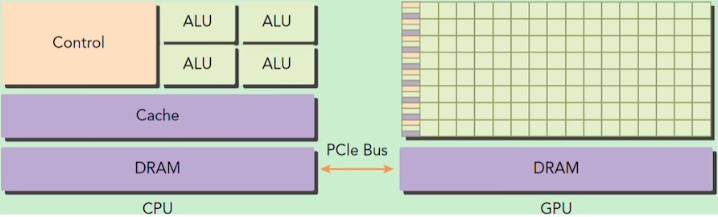
有一个很形象的关于CPU与GPU的话，同样来自SY__007

整体代码中splatting的部分全部使用cuda编写，一个线程负责一个像素，并发线程设计

并将整个图分为16*16的块，对每一个高斯划分区域，这样GPU的每一个block负责一个区，而block与block之间又可以共享内存，节省了显存

训练过程

核心目标是什么？

目标：给定一组已知相机参数的多视角图像，优化一组3D高斯体素，使得它们渲染出的图像与真实图像尽可能相似。

输入与初始化

输入数据：

一组图片 ${I_1,I_2,....,I_n}$

对应每张图的相机参数：

相机内参 $K_i$

相机外参 $R_i,T_i$ ,构成投影矩阵 $P_i=K_i[R_i|t_i]$

高斯体素初始化：

使用COLMAP 获得稀疏点云（SfM）初始化：

每个3D点初始为一个高斯体素
设置初始的协方差为球形，大小根据点密度估计。
初始颜色使用图像采样得到

💡3DGS不从零开始学习点的位置，而是从已知点云出发，加速收敛。

可学习参数：

每个高斯体素 $G_i$ 拥有一下可学习参数：

$\\mu_i$ : 三维空间中的中心位置

$\\sum _i$ : 协方差矩阵（控制体素形状/朝向/尺度）

$\\alpha_i$ : 不透明度（透明度决定是否遮挡其他体素）

$c_i$ : RGB颜色

$o_i$ : 光照相关参数（可选）

训练流程

我们按一个Epoch解析训练流程：

Step1:选取batch

通常一次从多个视角中抽取1~8张图像作为batch

Step2：渲染图像（forward pass）

使用当前高斯体素，通过可微光栅化渲染每张视角图像：

$\\hat{I_{i}}=Render(G,P_i)$

使用GPU实现的rasterizer，生成预测图像 $\\hat{I_i}$

Step3:损失计算

对每张渲染图像与真实图像计算损失：

$L = \\sum_{i} \\lambda_{l2} \\cdot \\|\\hat{I}_i - I_i\\|^2 + \\lambda_{reg} \\cdot L_{\\text{regularization}}$

常用的损失包括：

L2/MSE 图像像素级差异

SSIM 结构相似性指标，鼓励结构保留

LPIPS 感知损失，鼓励纹理和细节还原

透明度正则控制α防止梯度爆炸

Scale/shape正则保持体素大小不变形或坍塌

Step4：反向传播&参数更新

自动求导，对所有高斯参数进行反向传播。

使用优化器（如Adam等）更新每一个体素的参数：

<img alt=\"\\theta_{t+1}

训练期间的技巧与工程策略

1.Alpha截断和阈值：

低透明度的高斯体素将被剔除
阈值可逐步调整（从保守-->激进）(原代码中未进行调整，采用固定值0.005)

代码来自scene/gaussians.py ---> def prune_gaussians(self):

def prune_points(self, mask): valid_points_mask = ~mask optimizable_tensors = self._prune_optimizer(valid_points_mask) self._xyz = optimizable_tensors[\"xyz\"] self._features_dc = optimizable_tensors[\"f_dc\"] self._features_rest = optimizable_tensors[\"f_rest\"] self._opacity = optimizable_tensors[\"opacity\"] self._scaling = optimizable_tensors[\"scaling\"] self._rotation = optimizable_tensors[\"rotation\"] self.xyz_gradient_accum = self.xyz_gradient_accum[valid_points_mask] self.denom = self.denom[valid_points_mask] self.max_radii2D = self.max_radii2D[valid_points_mask] self.tmp_radii = self.tmp_radii[valid_points_mask]

实现逻辑如下：

mask = self.opacities.data >= opacity_thresholdself._prune(mask)

在train.py中，每N轮进行一次剔除：

if iteration % prune_interval == 0: scene.gaussians.prune_gaussians(opacity_threshold=cfg.alpha_thresh)

2.Adaptive Densification（动态密度增长）

初始点云稀疏，细节不够-->动态插值新的体素：

根据residual或遮挡区域添加新体素
类似NeRF的coarse-to-fine学习（由粗到细）

代码来自scene/gaussians.py --->densify_and_split/clone/prune

def densify_and_split(self, grads, grad_threshold, scene_extent, N=2): \"\"\" 对满足梯度条件的高斯点进行分裂操作，增加场景中复杂区域的高斯点密度 Args: grads: 高斯点的梯度信息，用于判断是否需要分裂 grad_threshold: 梯度阈值，超过此值的点可能需要分裂 scene_extent: 场景范围，用于判断高斯点大小是否合适 N: 每个选中的高斯点要分裂成的新点数，默认值为2 \"\"\" n_init_points = self.get_xyz.shape[0] # 获取当前高斯点的总数 # 处理梯度张量，确保其长度与高斯点数量一致（填充0） padded_grad = torch.zeros((n_init_points), device=\"cuda\") padded_grad[:grads.shape[0]] = grads.squeeze() # 筛选出满足梯度条件的高斯点： # 1. 梯度大于等于阈值 # 2. 高斯点的最大尺度大于场景范围的特定比例（表示该点可能过大，需要分裂） selected_pts_mask = torch.where(padded_grad >= grad_threshold, True, False) selected_pts_mask = torch.logical_and( selected_pts_mask, torch.max(self.get_scaling, dim=1).values > self.percent_dense * scene_extent ) # 为分裂的新点生成参数 # 缩放参数：原缩放的1/(0.8*N)，并应用逆激活函数 stds = self.get_scaling[selected_pts_mask].repeat(N, 1) means = torch.zeros((stds.size(0), 3), device=\"cuda\") # 零均值 samples = torch.normal(mean=means, std=stds) # 基于缩放的正态分布采样 # 旋转参数：复用原旋转并重复N次 rots = build_rotation(self._rotation[selected_pts_mask]).repeat(N, 1, 1) # 新点坐标：将采样点通过旋转矩阵变换后，加上原坐标（在局部坐标系中生成新点） new_xyz = torch.bmm(rots, samples.unsqueeze(-1)).squeeze(-1) + self.get_xyz[selected_pts_mask].repeat(N, 1) # 其他参数：继承原高斯点的属性并适当调整 new_scaling = self.scaling_inverse_activation(self.get_scaling[selected_pts_mask].repeat(N, 1) / (0.8 * N)) new_rotation = self._rotation[selected_pts_mask].repeat(N, 1) new_features_dc = self._features_dc[selected_pts_mask].repeat(N, 1, 1) # 直流分量特征 new_features_rest = self._features_rest[selected_pts_mask].repeat(N, 1, 1) # 其余频率分量特征 new_opacity = self._opacity[selected_pts_mask].repeat(N, 1) # 不透明度 new_tmp_radii = self.tmp_radii[selected_pts_mask].repeat(N) # 临时半径 # 将新生成的高斯点添加到模型中 self.densification_postfix(new_xyz, new_features_dc, new_features_rest, new_opacity, new_scaling, new_rotation, new_tmp_radii) # 构建修剪过滤器：原选中的点需要被修剪（已分裂成新点），新生成的点保留 prune_filter = torch.cat(( selected_pts_mask, torch.zeros(N * selected_pts_mask.sum(), device=\"cuda\", dtype=bool) )) self.prune_points(prune_filter) # 执行修剪操作def densify_and_clone(self, grads, grad_threshold, scene_extent): \"\"\" 对满足梯度条件的高斯点进行克隆操作，在需要更精细表示的区域增加相同的高斯点 Args: grads: 高斯点的梯度信息 grad_threshold: 梯度阈值 scene_extent: 场景范围 \"\"\" # 筛选出满足梯度条件的高斯点： # 1. 梯度范数大于等于阈值 # 2. 高斯点的最大尺度小于等于场景范围的特定比例（表示该点可能过小，需要克隆） selected_pts_mask = torch.where(torch.norm(grads, dim=-1) >= grad_threshold, True, False) selected_pts_mask = torch.logical_and( selected_pts_mask, torch.max(self.get_scaling, dim=1).values <= self.percent_dense * scene_extent ) # 克隆选中的高斯点（参数完全相同） new_xyz = self._xyz[selected_pts_mask] new_features_dc = self._features_dc[selected_pts_mask] new_features_rest = self._features_rest[selected_pts_mask] new_opacities = self._opacity[selected_pts_mask] new_scaling = self._scaling[selected_pts_mask] new_rotation = self._rotation[selected_pts_mask] new_tmp_radii = self.tmp_radii[selected_pts_mask] # 将克隆的高斯点添加到模型中 self.densification_postfix(new_xyz, new_features_dc, new_features_rest, new_opacities, new_scaling, new_rotation, new_tmp_radii)def densify_and_prune(self, max_grad, min_opacity, extent, max_screen_size, radii): \"\"\" 综合执行高斯点的克隆、分裂和修剪操作，动态调整场景中高斯点的密度 Args: max_grad: 梯度最大值，用于判断是否需要克隆或分裂 min_opacity: 最小不透明度阈值，低于此值的点会被修剪 extent: 场景范围 max_screen_size: 屏幕空间中高斯点的最大尺寸阈值 radii: 高斯点的半径信息 \"\"\" # 计算平均梯度（累积梯度除以计数） grads = self.xyz_gradient_accum / self.denom grads[grads.isnan()] = 0.0 # 处理NaN值 # 执行克隆和分裂操作 self.tmp_radii = radii self.densify_and_clone(grads, max_grad, extent) # 克隆操作 self.densify_and_split(grads, max_grad, extent) # 分裂操作 # 构建修剪掩码：不透明度低于阈值的点会被修剪 prune_mask = (self.get_opacity  max_screen_size # 视口空间中过大的点 big_points_ws = self.get_scaling.max(dim=1).values > 0.1 * extent # 世界空间中过大的点 prune_mask = torch.logical_or(torch.logical_or(prune_mask, big_points_vs), big_points_ws) # 执行修剪操作 self.prune_points(prune_mask) tmp_radii = self.tmp_radii self.tmp_radii = None # 清理GPU缓存 torch.cuda.empty_cache()def add_densification_stats(self, viewspace_point_tensor, update_filter): \"\"\" 累积高斯点的梯度统计信息，为后续的密度调整（克隆/分裂）提供依据 Args: viewspace_point_tensor: 视图空间中的点张量 update_filter: 指示哪些点需要更新梯度统计的过滤器 \"\"\" # 累积视图空间中x和y方向的梯度范数 self.xyz_gradient_accum[update_filter] += torch.norm(viewspace_point_tensor.grad[update_filter, :2], dim=-1, keepdim=True) self.denom[update_filter] += 1 # 累积计数，用于计算平均梯度

3.屏幕空间Culling(加速训练)

渲染时仅考虑投影在图像内的体素
使用bounding-box、depth-range提前裁剪

实现在 CUDA 扩展模块中：diff-gaussian-rasterization/cuda_rasterizer/backward.cu 与forward.cu 中，有条件判断是否渲染该体素

template__global__ void preprocessCUDA(...){ auto idx = cg::this_grid().thread_rank(); // 当前处理的高斯索引 if (idx >= P) // 若索引超出高斯总数，直接返回 return; // 初始化半径和覆盖瓦片数为0（若未更新，该高斯会被默认剔除） radii[idx] = 0; tiles_touched[idx] = 0; // 视锥体剔除：检查高斯是否在相机视锥体内（包括近裁剪） // 若不在视锥体内，直接返回（剔除该高斯） float3 p_view; if (!in_frustum(idx, orig_points, viewmatrix, projmatrix, prefiltered, p_view)) return; // （中间省略：高斯3D->2D投影、协方差计算等） // 计算高斯在屏幕空间的投影中心和覆盖半径 float2 point_image = { ndc2Pix(p_proj.x, W), ndc2Pix(p_proj.y, H) }; uint2 rect_min, rect_max; // 计算高斯在屏幕上覆盖的像素矩形范围（min/max坐标） getRect(point_image, my_radius, rect_min, rect_max, grid); // 屏幕空间范围剔除：若覆盖的矩形区域面积为0（不覆盖任何像素），则剔除 if ((rect_max.x - rect_min.x) * (rect_max.y - rect_min.y) == 0) return; // （后续：保存高斯的渲染所需数据，参与后续光栅化） radii[idx] = my_radius; points_xy_image[idx] = point_image; // ... 其他数据存储}

4.LOD（Level-of-Detail）调整

训练阶段采取更高分辨率
渲染阶段可用多分辨率合成图像，提升速度与质量

代码在train.py中体现的很清楚

resolution_schedule = [ (0, 400), (2000, 800), (4000, 1024), ...]def getTrainResolution(step): for s, res in reversed(resolution_schedule): if step >= s: return res

通过OpenGL窗口或CUDA投影传递给渲染器，从而决定屏幕空间尺寸（W,H）、每个高斯的足迹（由像素大小影响）、getReac()计算的tile覆盖范围

3DGS出现的问题

1.Alpha截断策略不完善

原版中采用固定阈值（0.005）对透明高斯剔除

这样静态的设置容易误删潜在有用的高四点，或者保留冗余点，影响收敛效率与渲染质量

改进方法：

使用软阈值+可学习，避免硬截断。

典型工作：GGS、SC-GS

2.Densification策略过于盲目

每N步均匀插入新高斯，密度扩张基于启发式

这样缺少任务驱动性与学习性，不能自适应任务难度或视角覆盖度，造成资源浪费

改进方法：

误差驱动density（重建误差高处增加点）
衰减或合并冗余点

典型工作：GGS（残差驱动）、Mip-3DGS(基于层级密度)

3.优化流程不稳定

早期使用Adam+特殊正则约束（如位置约束、球面约束等）

这样高斯之间缺乏明确的结构约束，容易出现重复点、飘移、模糊融合，特别是在边缘或高频区域

改进方法：

邻域结构正则化、引入显示几何结构引导、高斯稀疏化与融合控制、引入 Embedding或语义anchor

典型工作：GGS、SC-GS、SimGS

4.难以处理动态场景

原版的3DGS假设是静态场景，所有的高斯的位置和属性在整个时间序列中是固定的。

这样无法建模物体运动或相机运动导致的动态变化，限制了其在视频、4D场景等任务中的应用

改进方法：

给每一个高斯绑定一个轨迹函数，并使用时间编码进行时序建模

典型工作：

4DGS（显式控制）

GauSim(使用贝塞尔轨迹建模可学习运动)

DynGS（物体级运动建模）

5.对遮挡与深度模糊处理不佳

采用前向splatting投影到图像平面，对深度排序较敏感

这样多物体遮挡区域或高深度梯度区域容易出现artifacts（如ghosting、模糊边缘）

改进方法：

Soft visibility：采用softmax-based alpha blending 替代depth sort

Masked loss:遮挡区域增加mask监督

典型工作：VoGS、NeuSplat（借助光线可见性）

6.不具备语义可控性或结构表达能力

每个高斯是独立、孤立的点，没有结构信息

这样对编辑或语义控制力差

改进方法：

使用learnable instanceID embedding

聚类算法辅助生成 semantic-aware Gaussians

典型工作： SC-GS、SimGS

7.全图高斯遍历效率低

即使使用view frustum culling 等筛选策略，但在高分辨率或大场景下仍计算冗余

这样渲染速度与高斯数量线性相关，难以scale到高密度场景

改进方法：

LOD：构建多尺度高斯树结构，远处使用低精度

屏幕空间裁剪：只投影到当前帧可见区域

典型工作：Mip-3DGS、GGS

8.精度强烈依赖于SfM初始化精度

一旦SfM的pose不准/点云系数或错位，后续优化直接崩盘

改进方法：

Pose refinement（在训练中微调camera pose）----- GGS-Pose/Neuralangelo

多视角一致性监督 ----- Mip-3DGS、SimGS

典型工作： VGGT+3dgs

你再也找不到更详细的3DGS教程了 —— 一万九千字长文解析3DGS_3dgs 透视投影

做雪球?

What is splatting？

为什么这是一个椭球？

抛雪球

如何进行参数变换？

观测变换

投影变换

正交投影：

透视投影：

视口变换：

视口变换的数学实现

视口变换的实际作用：

光栅化：

1.光栅化的位置：渲染管线‘矢量-->像素’转换

2.光栅化的核心任务:图元的“离散化”

3.光栅化的关键步骤

雅可比矩阵怎么求？

足迹渲染（footprint）？

什么是footprint？

Footprint渲染流程

1.高斯体素的投影

2.按屏幕空间进行排序(Z-buffer Trick)

3.渲染：Rasterization by Splatting

4.足迹渲染的优势

5.可微性分析

雪球颜色：

相关基础概念：

球谐函数的应用

为什么球谐函数可以更好的表达颜色？

合成图片

像素的颜色

3DGS为什么快？

训练过程

核心目标是什么？

输入与初始化

输入数据：

高斯体素初始化：

可学习参数：

训练流程

Step1:选取batch

Step2：渲染图像（forward pass）

Step3:损失计算

Step4：反向传播&参数更新

训练期间的技巧与工程策略

1.Alpha截断和阈值：

2.Adaptive Densification（动态密度增长）

3.屏幕空间Culling(加速训练)

4.LOD（Level-of-Detail）调整

3DGS出现的问题

1.Alpha截断策略不完善

2.Densification策略过于盲目

3.优化流程不稳定

4.难以处理动态场景

5.对遮挡与深度模糊处理不佳

6.不具备语义可控性或结构表达能力

7.全图高斯遍历效率低

8.精度强烈依赖于SfM初始化精度

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载