进阶数据结构： AVL树

嘿，各位技术潮人！好久不见甚是想念。生活就像一场奇妙冒险，而编程就是那把超酷的万能钥匙。此刻，阳光洒在键盘上，灵感在指尖跳跃，让我们抛开一切束缚，给平淡日子加点料，注入满满的passion。准备好和我一起冲进代码的奇幻宇宙了吗？Let\'s go！

我的博客：yuanManGan

我的专栏：C++入门小馆 C言雅韵集 数据结构漫游记  闲言碎语小记坊 题山采玉 领略算法真谛

目录

AVL相关概念：

 AVL树的结构

Insert

 旋转

右旋：

​编辑

左单旋：

 右左双旋：

左右双旋：

 完整的插入：

其他简单的操作： 

测试：

AVL相关概念：

AVL树是由二叉搜索树加上一定的限制而形成的树，AVL树：它的左右子树都是AVL树，且左右子树的高度差的绝对值不超过1。AVL树是⼀颗⾼度平衡搜索⼆叉树， 通过控制⾼度差去控制平衡。

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis是两个前苏联的科学家，他们在1962 年的论⽂《An algorithm for the organization of information》中发表了它。

AVL树引入了平衡因子这个概念，每个节点都有平衡因子，任何节点的平衡因子等于右子树的高度减去左子树的高度，也就是说AVL树的每个节点的平衡因子等于1/-1/0，但AVL树不是必须要平衡因子，但引入平衡因子能让我们更方便去观察和控制树是否平衡。

AVL因为它的平衡条件，使得我们树的高度可以控制在logN，那么搜索的时间复杂度也就是logN咯，相比于二叉搜索树有了质的提升。

 AVL树的结构

#includeusing namespace std;templatestruct AVLTreeNode{pair _kv;AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;int _bf;//平衡因子AVLTreeNode(pair kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), bf(0){ }};templateclass AVLTree{typedef AVLTreeNode Node;public://...private:Node* _root = nullptr;};

Insert

我们要插入一个值在AVL树中的前半过程和二叉平衡树一样，都是先找到要插入的位置然后插入，插入后就有一点不一样了，在AVL树中最重要的要进行更新平衡因子，也就是_bf。

平衡因子的更新：

平衡因⼦ = 右⼦树⾼度-左⼦树⾼度，只有子树发生了变换我们才会影响平衡因子，也就是我们插入节点，会增加高度，如果我们插入的节点在parent的右侧parent的平衡因子++，反之--，parent的变化也影响着我们是否要继续向上更新平衡因子。 1.更新过后parent的平衡因子等于0 更新中parent的平衡因⼦变化为-1->0 或者 1->0，说明更新前 parent⼦树⼀边⾼⼀边低，新增的结点插⼊在低的那边，插⼊后parent所在的⼦树⾼度不变，不会 影响parent的⽗亲结点的平衡因⼦，更新结束。

2.更新后parent的平衡因⼦等于1 或 -1 更新前更新中parent的平衡因⼦变化为0->1 或者 0->-1， 说 明更新前parent⼦树两边⼀样⾼，新增的插⼊结点后，parent所在的⼦树⼀边⾼⼀边低，parent所 在的⼦树符合平衡要求，但是⾼度增加了1，会影响parent的⽗亲结点的平衡因⼦，所以要继续向 上更新。

3.更新后parent的平衡因⼦等于2 或 -2 更新前更新中parent的平衡因⼦变化为1->2 或者 -1->-2，说 明更新前parent⼦树⼀边⾼⼀边低，新增的插⼊结点在⾼的那边，parent所在的⼦树⾼的那边更⾼ 了，破坏了平衡，parent所在的⼦树不符合平衡要求，需要旋转处理，旋转的⽬标有两个：1、把 parent⼦树旋转平衡。2、降低parent⼦树的⾼度，恢复到插⼊结点以前的⾼度。所以旋转后也不 需要继续往上更新，插⼊结束

4.不断更新，更新到根，跟的平衡因⼦是1或-1也停⽌了。

 插⼊结点及更新平衡因⼦的代码实现：

bool Insert(pair kv){Node* cur = _root;Node* parent = nullptr;//插入操作while (cur){if (cur->_kv.first _right;}else if(cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//插入失败return false;}}cur = new Node(kv);if (parent->_kv.first _right = cur;}elseparent->_left = cur;cur->_parent = parent;//更新平衡因子while (parent){if (cur = parent->_right){parent->_bf++;}else if (cur = parent->_left){parent->_bf--;}if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){//继续更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转操作//...break;}else assert(false);}return true;}

 旋转

右旋：

当出现这种情况时，我们可以将根节点拿下来称为3节点的右树，

这就叫作右旋，我们再一般化一下：

我们仅仅需要改变三个节点的指向就可以了。

当parent的平衡因子为-2且cur的平衡因子为-1的时候就右旋，将根节点旋下来，将subL的右子树给parent的左子树。

实现如下：

void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* ppnode = parent->_parent;if (subLR)subLR->_parent = parent;parent->_left = subLR;parent->_parent = subL;subL->_right = parent;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{subL->_parent = ppnode;if (ppnode->_right = parent)ppnode->_right = subL;else ifppnode->_left = subL;}parent->_bf = subL->_bf = 0;}

左单旋：

左单旋就是一样的思路咯，就不一一继续赘述了，当parent的平衡因子等于2且cur的平衡因子等于1时要进行左单旋。

代码：

void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subL->_left;Node* ppnode = parent->_parent;if (subRL)subRL->_parent = parent;parent->_right = subRL;parent->_parent = subR;subR->_left = parent;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{subR->_parent = ppnode;if (ppnode->_right = parent)ppnode->_right = subR;else ifppnode->_left = subR;}parent->_bf = subR->_bf = 0;}

 右左双旋：

当出现这种情况时，我们无论是左单旋还是右单旋，都无法将它变成AVL平衡树， 

将它左旋只会就成了这个玩意。

我们正确的解决方法是什么呢 我们可以将5节点进行右旋，最后左旋3号节点：

我们再来特殊化处理一下：

但我们在b点插入还有点讲究：

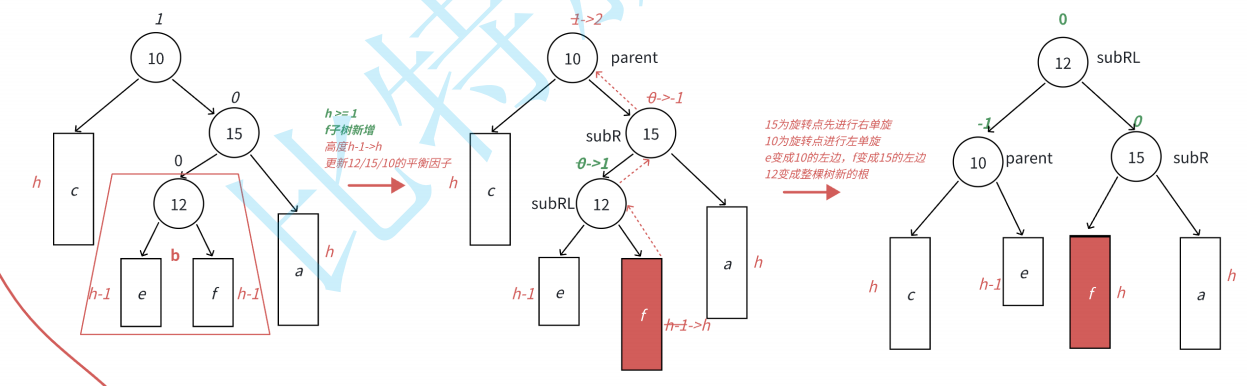
 这是三种情况，我们就来实现一下代码吧：

void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1){subRL->_bf = subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = parent->_bf = 0;subR->_bf = -1;}else if (bf == 0){parent->_bf = subR->_bf = 0;}else{assert(false);}}

同样的 来看看

左右双旋：

代码如下：

void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subR->_right;int bf = subRL->_bf;RotateR(subL);RotateL(parent);if (bf == 1){subLR->_bf = subL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subLR->_bf = parent->_bf = 0;subL->_bf = -1;}else if (bf == 0){parent->_bf = subL->_bf = 0;}else{assert(false);}}

 完整的插入：

bool Insert(const pair& kv){if (_root == nullptr) // 新增：处理根节点为空{_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;//插入操作while (cur){if (cur->_kv.first _right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//插入失败return false;}}cur = new Node(kv);if (parent->_kv.first _right = cur;}elseparent->_left = cur;cur->_parent = parent;//更新平衡因子while (parent){if (cur == parent->_right){parent->_bf++;}else if (cur == parent->_left){parent->_bf--;}if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){//继续更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1)RotateR(parent);else if (parent->_bf == 2 && cur->_bf == 1)RotateL(parent);else if (parent->_bf == -2 && cur->_bf == 1)RotateLR(parent);else if (parent->_bf == 2 && cur->_bf == -1)RotateRL(parent);break;}else assert(false);}return true;}

其他简单的操作： 

Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first _right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);cout <_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool _IsBalanceTree(Node* root){// 空树也是AVL树if (nullptr == root)return true;// 计算pRoot结点的平衡因子：即pRoot左右子树的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者// pRoot平衡因子的绝对值超过1，则一定不是AVL树if (abs(diff) >= 2){cout <_kv.first << \"高度差异常\" <_bf != diff){cout <_kv.first << \"平衡因子异常\" <_left) && _IsBalanceTree(root->_right);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout <_kv.first <_right);}

测试：

#define _CRT_SECURE_NO_WARNINGS 1#includeusing namespace std;#include\"AVLTree.h\"// 测试代码void TestAVLTree1(){ AVLTree t; // 常规的测试用例 //int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 }; // 特殊的带有双旋场景的测试用例 int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 }; for (auto e : a) { if (e == 18) { int x = 0; } t.Insert({ e, e }); std::cout << \"Insert\" << e <\"; cout << t.IsBalanceTree() << endl; } t.InOrder(); cout << t.IsBalanceTree() << endl;}#include// 插入一堆随机值，测试平衡，顺便测试一下高度和性能等void TestAVLTree2(){ const int N = 10000000; vector v; v.reserve(N); srand(time(0)); for (size_t i = 0; i < N; i++) { v.push_back(rand() + i); } size_t begin2 = clock(); AVLTree t; for (auto e : v) { t.Insert(make_pair(e, e)); } size_t end2 = clock(); cout << \"Insert:\" << end2 - begin2 << endl; cout << t.IsBalanceTree() << endl; cout << \"Height:\" << t.Height() << endl; cout << \"Size:\" << t.Size() << endl; size_t begin1 = clock(); // 确定在的值 /*for (auto e : v) { t.Find(e); }*/ // 随机值 for (size_t i = 0; i < N; i++) { t.Find((rand() + i)); } size_t end1 = clock(); cout << \"Find:\" << end1 - begin1 << endl;}int main(){ TestAVLTree2(); return 0;}