一、题目解析

1、将给定升序链表合并,依旧升序排列
2、链表个数可为0,并会出现空指针的情况
二、算法原理
解法1:暴力解法 O(N*K^2)
按合并两个有序链表,两两合并

解法2:利用优先级队列优化 O(N*K*logK)
优先级队列默认是大根堆,我们是升序合并,所以我们需要传入比较函数,修改为小根堆
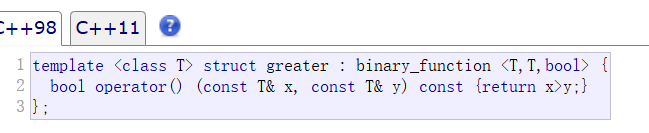
由于我们存储的是链表的指针,所以模板提供的greater不符合我们的比较逻辑,这里给出两个方法
1、自己实现一个仿函数,重写比较规则
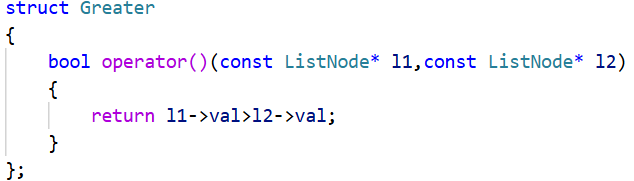
2、重载operator>(不建议,因为是ListNode类中成员函数,题目提供了ListNode类)
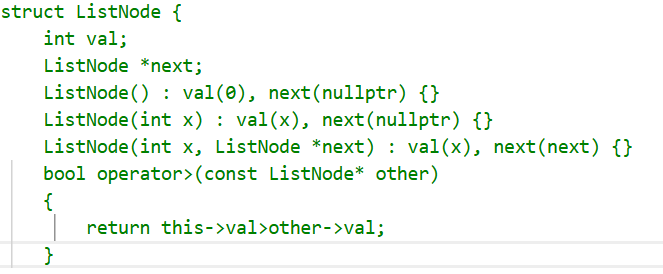

第三个模板参数要求传递的是类型,lambda表达式是一个匿名函数对象,所以不能用lambda表达式
具体流程:
1、先建k个(lists.size())小根堆(注意:建堆时,需要判断指针是否为空,为空则不插入)
2、用top()取出堆顶元素链接到哨兵位头结点上
3、若堆顶元素的next不为空,则push()到小根堆中,直到小根堆中元素为空
时间复杂度分析:
由于k个小根堆,堆排时间复杂为logK,需要遍历平均长度为n的k个链表n*k,所以总的时间复杂度为logk*k*n
解法3:分治-递归 O(N*K*logK)
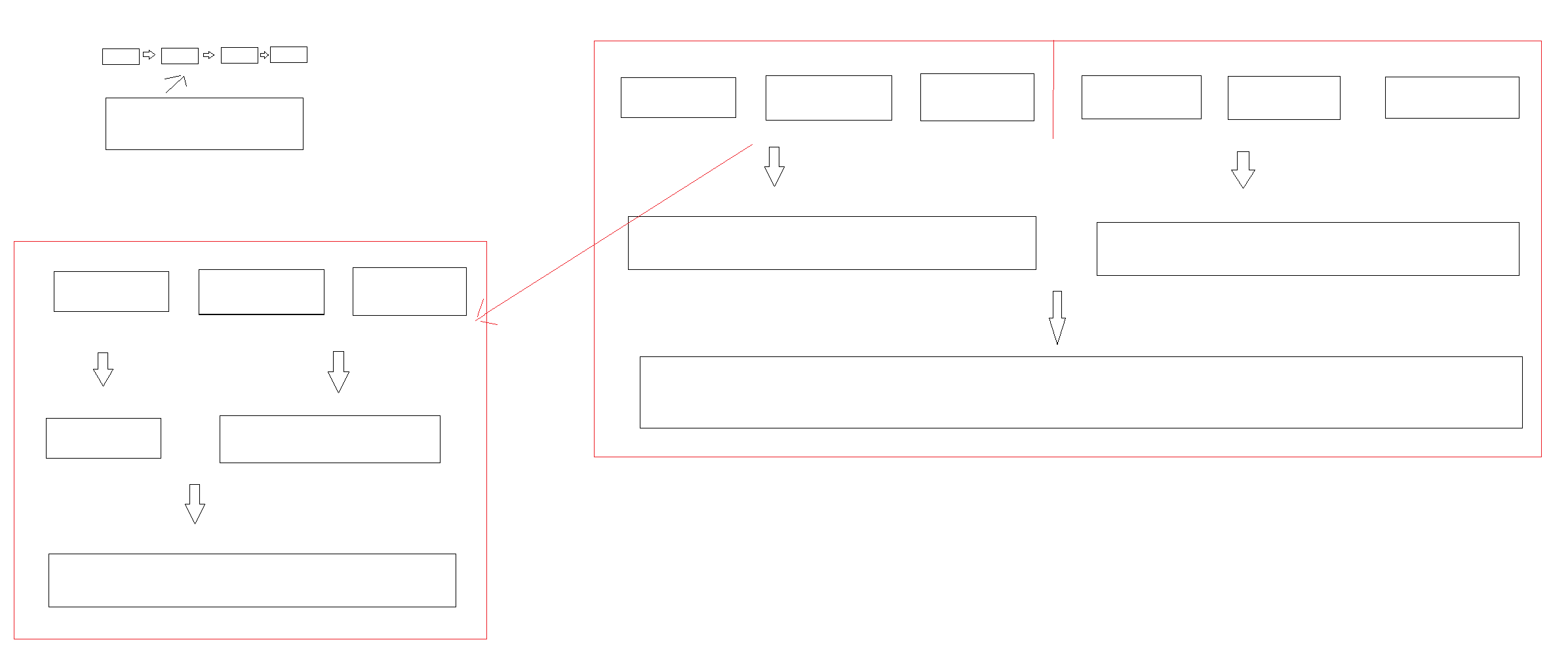
两个红框内的合并逻辑是一样的,所以可以使用分治递归的方法实现
时间复杂度分析:
每次合并所需logk,n的平均长度的k个链表,所需时间为logK*K*N
三、代码示例
解法2:
//解法2:优先级队列优化class Solution {public: struct Greater { bool operator()(const ListNode* l1,const ListNode* l2) { return l1->val>l2->val; } }; ListNode* mergeKLists(vector& lists) { const int k = lists.size(); priority_queue<ListNode*,vector,Greater> pq;//建小根堆 ListNode* newhead = new ListNode(); //传入k个节点指针 for(auto e : lists) { if(e) pq.push(e); if(pq.size()>k) pq.pop(); } ListNode* tail = newhead; //开始合并 while(!pq.empty()) { ListNode* newnode = pq.top(); pq.pop(); //判断是否插入后一个节点指针 if(newnode && newnode->next != nullptr) pq.push(newnode->next); //链接 tail->next = newnode; tail = newnode; } ListNode* cur = newhead->next; delete newhead;//释放哨兵位头结点 return cur; }};
解法3:
//解法3:分治-归并class Solution {public: ListNode* mergeKLists(vector& lists) { //特判没有元素的情况 if(lists.empty()) return nullptr; return mergeSort(lists,0,lists.size()-1); } ListNode* mergeSort(vector& lists,int left,int right) { //只有一个元素时返回 if(left>=right) return lists[right]; //分两块块[left,mid][mid+1,right] int mid = (left+right)>>1; ListNode* cur1 = mergeSort(lists,left,mid); ListNode* cur2 = mergeSort(lists,mid+1,right); //合并两个有序链表 ListNode* newhead = new ListNode(); ListNode* tail = newhead; while(cur1&&cur2) { if(cur1->val>cur2->val) { tail->next = cur2; tail = cur2; cur2=cur2->next; } else { tail->next = cur1; tail = cur1; cur1=cur1->next; } } //处理未合并完的链表 while(cur1) { tail->next = cur1; tail = cur1; cur1=cur1->next; } while(cur2) { tail->next = cur2; tail = cur2; cur2=cur2->next; } tail = newhead->next; delete newhead;//释放哨兵位头结点 return tail; }};
看到最后,如果对您有所帮助,还请点赞、收藏和关注,我们下期再见!











