数据结构入门：详解顺序表的实现与操作_一、线性表 二、顺序表 2.1 概念与结构 2.2 分类 2.2.1 静态顺序表 2.2.2 动态顺

目录

1.线性表

2.顺序表

2.1概念与结构

2.2分类

2.2.1静态顺序表

2.2.2动态顺序表 

3.动态顺序表的实现

3.1.SeqList.h

3.2.SeqList.c

3.2.1初始化

 3.2.2销毁

3.2.3打印

3.2.4顺序表扩容 

3.2.5尾部插入及尾部删除 

3.2.6头部插入及头部删除 

3.2.7特定位置插入及删除 

3.2.8查找元素，返回下标 

 4.顺序表算法题

1.力扣：移除元素

核心思想

算法步骤

 2.力扣：删除有序数组的重复项

核心思想

算法步骤

 3.力扣：合并两个有序数组

核心思想

算法步骤

---

1.线性表

在讲顺序表之前，我们首先要介绍一个概念，线性表。

线性表（Linear List）是数据结构中最基础、最常用的一种结构，它的特点是数据元素之间按线性顺序排列，每个元素最多有一个前驱和一个后继。

线性表有两种实现方式，其一是顺序表，其二是链表。以下我们来为他们做一个简单区分：

顺序表（顺序存储） 链表（链式存储） 实现方式 用数组存储元素，内存连续分配 用结点存储元素和指针，内存非连续分配 特点

• 支持随机访问（通过下标直接访问元素，时间复杂度 O(1)）。

• 插入/删除可能需要移动大量元素（时间复杂度 O(n)）。

• 存储空间固定（需预先分配，可能浪费或不足）。

• 插入/删除高效（时间复杂度 O(1)，仅需修改指针）。

• 不支持随机访问（查找需从头遍历，时间复杂度 O(n)）。

• 存储空间动态分配，更灵活。

适用场景 元素数量固定、频繁查询、少增删。 频繁增删、元素数量变化大。

表格内容暂时看不明白没有关系，这里只是做一个简介，相信等你看完博客之后会有一个新的体会。

今天我们着重介绍的是顺序表，链表会放在下一篇博客中精讲。

---

2.顺序表

2.1概念与结构

概念：顺序表是⽤⼀段物理地址连续的存储单元依次存储数据元素的线性结构，⼀般情况下采⽤数组存储。

顺序表和数组的区别？ 

顺序表是数据结构中线性表的一种实现方式，本质是基于数组的封装，通过数组实现元素的连续存储，并添加了对数据操作的逻辑（如插入、删除、扩容等）。

2.2分类

2.2.1静态顺序表

定义与特点

• 固定容量：在创建时分配固定大小的内存空间，无法动态扩展或收缩。

• 内存分配：通常在编译阶段确定（如全局数组）或在栈上分配（如局部数组），内存管理由系统自动完成。

• 操作限制：仅支持基本的读写操作，插入和删除需手动移动元素，效率较低。

#define SLDataType int // 定义顺序表元素类型为int（便于后期类型修改）#define N 7  // 定义顺序表容量为7（固定大小）// 静态顺序表结构体定义typedef struct Seqlist { // 类型重命名为SL SLDataType arr[N]; // 固定大小的数组存储元素 int size; // 记录当前有效元素个数（核心状态标识）} SL;  // 类型重命名简化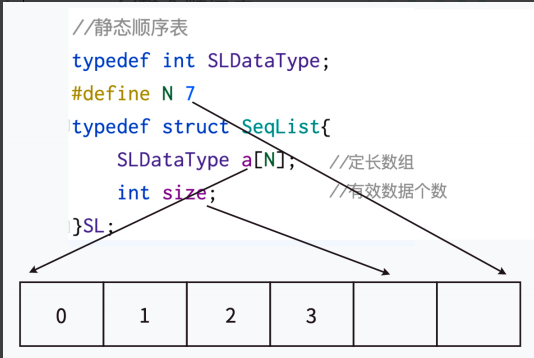

2.2.2动态顺序表 

 定义与特点

• 可变容量：支持运行时动态调整容量（扩展或收缩），通过重新分配内存实现。

• 内存分配：通常在堆上动态分配，由程序逻辑管理（如 malloc 或 new）。

• 高级操作：封装了插入、删除、扩容等复杂逻辑，用户无需手动处理内存。

// 定义顺序表存储的元素类型为int// 使用宏定义方便后续修改元素类型（例如改为float或自定义结构体）#define SLDataType int // 动态顺序表结构体定义typedef struct Seqlist { SLDataType* arr; // 指向动态分配数组的指针（存储元素） int size; // 当前顺序表中有效元素的数量 int capacity; // 当前顺序表的总容量} SL; // 使用typedef将结构体重命名为SL，简化代码

将静态顺序表和动态数据表做一个对比：

特性 静态顺序表 动态顺序表 存储方式 固定大小数组（栈内存/全局区） 动态分配数组（堆内存） 容量 编译时确定（#define N 7），不可变 运行时动态调整（通过malloc/realloc） 内存分配 自动分配和释放（无需手动管理） 需手动管理（malloc/free） 扩容/缩容 不支持，大小固定 支持，可动态调整（如capacity不足时扩容）

经过比对，我们发现 

• 静态顺序表简单但僵化，适合确定性的小规模数据。

• 动态顺序表复杂但强大，是现代编程语言中动态数组的基础实现。

本文将以实现动态顺序表为主，详细讲述动态顺序表的扩容，头插，尾插，删除等操作。

---

3.动态顺序表的实现

3.1.SeqList.h

#pragma once#include#include#includetypedef int SLDataType;// 动态顺序表 -- 按需申请typedef struct SeqList{SLDataType* arr;int size; // 有效数据个数int capacity; // 空间容量}SL;//初始化和销毁void SLInit(SL* ps);void SLDestroy(SL* ps);void SLPrint(SL* ps);//扩容void SLCheckCapacity(SL* ps);//头部插⼊删除 / 尾部插⼊删除void SLPushBack(SL* ps, SLDataType x);void SLPopBack(SL* ps);void SLPushFront(SL* ps, SLDataType x);void SLPopFront(SL* ps);//指定位置之前插⼊/删除数据void SLInsert(SL* ps, int pos, SLDataType x);void SLErase(SL* ps, int pos);int SLFind(SL * ps, SLDataType x);

一个动态顺序表至少应该能够实现以上功能，下面我们来逐一实现。

3.2.SeqList.c

3.2.1初始化

void SLInit(SL* ps){ps->arr = NULL;ps->capacity = 0;ps->size = 0;}

 3.2.2销毁

void SLDestroy(SL* ps){if (ps->arr){free(ps->arr);}ps->arr = NULL;ps->capacity = 0;ps->size = 0;}

注意：这里释放空间需要判断指针是否为空，如果是空指针直接释放会报错，同时我们要检查的是ps->arr，并不是ps,需要额外注意，不要释放ps的空间和将ps置空指针

3.2.3打印

void SLPrint(SL* ps){for (int i = 0; i size; i++){printf(\"%d \", ps->arr[i]);}printf(\"\\n\");}

3.2.4顺序表扩容 

void SLCheckCapacity(SL* ps){ // 检查是否需要扩容（当前元素数 == 当前容量） if (ps->capacity == ps->size) { // 计算新容量：如果当前容量为0（初始状态）则设为4，否则扩容2倍 int new_capacity = ps->capacity == 0 ? 4 : 2 * (ps->capacity); // 尝试重新分配内存 SLDataType* tem = realloc(ps->arr, new_capacity * sizeof(SLDataType)); // 处理内存分配失败的情况 if (tem == NULL) { perror(\"realloc\"); // 打印错误信息 exit(EXIT_FAILURE); // 终止程序（EXIT_FAILURE是标准错误退出码） } // 更新顺序表结构 ps->arr = tem;  // 指向新分配的内存 ps->capacity = new_capacity; // 更新容量值 }}

关键点说明：

1. 扩容时机：

   • 当size == capacity时触发扩容，这是为了防止下一次插入操作导致溢出

2. 扩容策略：

   • 初始容量设为4（常见设计，避免初期频繁扩容）

   • 之后每次按2倍扩容（标准库常用策略，均摊时间复杂度为O(1)）

3. 内存管理：

   • 使用realloc而不是malloc，可以保留原有数据

   • 必须检查返回值是否为NULL（内存分配可能失败）

4. 错误处理：

   • 使用perror输出错误信息（会显示系统级的错误原因）

   • EXIT_FAILURE是标准库定义的错误退出码（通常值为1）

5. 安全性：

   • 先将realloc结果赋给临时变量tem，确认成功后再赋给ps->arr

   • 避免直接ps->arr = realloc(...)导致内存泄漏

3.2.5尾部插入及尾部删除 

/** * @brief 在顺序表尾部插入一个元素 * @param ps 指向顺序表结构的指针（必须非空） * @param x 要插入的元素值 */void SLPushBack(SL* ps, SLDataType x) { assert(ps);  // 确保顺序表指针有效（若ps为NULL则终止程序） SLCheckCapacity(ps); // 检查并扩容（若容量不足） ps->arr[ps->size++] = x; // 在尾部插入元素，并更新size}/** * @brief 删除顺序表尾部元素（逻辑删除） * @param ps 指向顺序表结构的指针（必须非空且arr有效） */void SLPopBack(SL* ps) { assert(ps && ps->arr); // 确保顺序表指针和内部数组指针均有效 ps->size--; // 减少size，忽略最后一个元素（逻辑删除）}

3.2.6头部插入及头部删除 

/** * @brief 在顺序表头部插入一个元素 * @param ps 指向顺序表结构的指针（必须非空且内部数组已初始化） * @param x 要插入的元素值 * @note 时间复杂度 O(n)，需要移动所有元素 */void SLPushFront(SL* ps, SLDataType x) { // 1. 参数校验 assert(ps && ps->arr); // 确保顺序表指针和内部数组指针有效 // 2. 容量检查（必要时扩容） SLCheckCapacity(ps); // 检查并处理容量不足的情况 // 3. 移动元素：从后往前逐个后移 for (int i = ps->size; i > 0; i--) { ps->arr[i] = ps->arr[i - 1]; // 将元素向后移动一位 } // 4. 插入新元素到头部 ps->arr[0] = x; // 在数组头部放入新元素 // 5. 更新元素计数 ps->size++; // 顺序表长度+1}/** * @brief 删除顺序表头部元素 * @param ps 指向顺序表结构的指针（必须非空且顺序表不为空） * @note 时间复杂度 O(n)，需要移动剩余所有元素 */void SLPopFront(SL* ps) { // 1. 参数校验 assert(ps && ps->size > 0); // 确保顺序表有效且不为空 // 2. 移动元素：从前往后逐个前移 for (int i = 0; i size - 1; i++) { ps->arr[i] = ps->arr[i + 1]; // 将元素向前移动一位 } // 3. 更新元素计数 ps->size--; // 顺序表长度-1 /* 可选：清零最后一个元素位置的值 ps->arr[ps->size] = 0; // 防止脏数据 */}

3.2.7特定位置插入及删除 

/** * @brief 在顺序表指定位置前插入元素 * @param ps 指向顺序表结构的指针（必须非空） * @param pos 要插入的位置索引（0 ≤ pos ≤ ps->size） * @param x 要插入的元素值 * @note 时间复杂度 O(n)，需要移动元素 * @note 边界情况： * - pos=0：相当于头部插入 * - pos=size：相当于尾部追加 */void SLInsert1(SL* ps, int pos, SLDataType x) { assert(ps); // 确保顺序表指针有效 assert(pos >= 0 && pos size); // 检查位置合法性 SLCheckCapacity(ps); // 检查并扩容（若容量不足） // 从后往前移动元素，腾出pos位置 for (int i = ps->size; i > pos; i--) { ps->arr[i] = ps->arr[i - 1]; // 元素后移 } ps->arr[pos] = x; // 在pos位置插入新元素 ps->size++; // 更新元素数量}/** * @brief 在顺序表指定位置后插入元素 * @param ps 指向顺序表结构的指针（必须非空） * @param pos 参考位置索引（0 ≤ pos size） * @param x 要插入的元素值 * @note 时间复杂度 O(n)，需要移动元素 * @note 边界情况： * - pos=0：在第一个元素后插入 * - pos=size-1：相当于尾部追加 */void SLInsert2(SL* ps, int pos, SLDataType x) { assert(ps); // 确保顺序表指针有效 assert(pos >= 0 && pos size); // 检查位置合法性 SLCheckCapacity(ps); // 检查并扩容 // 从后往前移动元素，腾出pos+1位置 for (int i = ps->size; i > pos + 1; i--) { ps->arr[i] = ps->arr[i - 1]; // 元素后移 } ps->arr[pos + 1] = x; // 在pos+1位置插入新元素 ps->size++; // 更新元素数量}/** * @brief 删除顺序表指定位置的元素 * @param ps 指向顺序表结构的指针（必须非空且顺序表非空） * @param pos 要删除的位置索引（0 ≤ pos size） * @note 时间复杂度 O(n)，需要移动元素 * @note 边界情况： * - pos=0：删除头部元素 * - pos=size-1：删除尾部元素 */void SLErase(SL* ps, SLDataType pos) { assert(ps && ps->size > 0); // 确保顺序表有效且非空 assert(pos >= 0 && pos size); // 检查位置合法性 // 从pos位置开始，用后续元素覆盖当前元素 for (int i = pos; i size - 1; i++) { ps->arr[i] = ps->arr[i + 1]; // 元素前移 } ps->size--; // 更新元素数量 /* 可选：清除残留数据（防止脏数据） ps->arr[ps->size] = 0; */}

3.2.8查找元素，返回下标 

/** * @brief 在顺序表中查找指定元素的位置 * @param ps 指向顺序表结构的指针（必须非空） * @param x 要查找的元素值 * @return 如果找到，返回元素的索引（0 ≤ index < size）； * 如果未找到，返回 -1 * @note 时间复杂度 O(n)，需要遍历数组 */int SLFind(SL* ps, SLDataType x) { assert(ps); // 确保顺序表指针有效 // 遍历顺序表查找元素 for (int i = 0; i size; i++) { if (ps->arr[i] == x) { return i; // 找到元素，返回索引 } } return -1; // 未找到元素}

---

 4.顺序表算法题

1.力扣：移除元素

核心思想

使用 双指针技巧：

• src（源指针）：遍历原始数组，检查每个元素。

• dst（目标指针）：记录非 val 元素的存储位置。

算法步骤

1. 初始化 src 和 dst 为 0。

2. 遍历数组：

   • 如果 nums[src] == val：跳过该元素（src++）。

   • 如果 nums[src] != val：将其复制到 nums[dst]，然后 src++ 和 dst++。

3. 最终 dst 的值即为新数组的长度。

代码：

int removeElement(int* nums, int numsSize, int val) { int src = 0,dst = 0; while(src<numsSize) { if(nums[src]==val) src++; else { nums[dst] = nums[src]; dst++;src++; } } return dst;}

 2.力扣：删除有序数组的重复项

核心思想

使用 双指针技巧：

• dst（目标指针）：记录唯一元素的存储位置。

• src（源指针）：遍历数组，寻找与 dst 不同的元素。

算法步骤

1. 初始化 dst = 0（第一个元素必定唯一），src = 1。

2. 遍历数组：

   • 如果 nums[dst] == nums[src]：跳过重复元素（src++）。

   • 如果 nums[dst] != nums[src]：将 nums[src] 复制到 nums[++dst]，然后 src++。

3. 最终 dst + 1 即为新数组的长度（因为索引从 0 开始）。

 代码：

int removeDuplicates(int* nums, int numsSize) { int dst = 0,src = 1; while(src<numsSize) { if(nums[dst]==nums[src]) { src++; } else { nums[++dst] = nums[src++]; } } return dst+1;}

 3.力扣：合并两个有序数组

核心思想

使用 逆向双指针法 从后向前合并，避免覆盖 nums1 中的未处理元素。

算法步骤

1. 初始化指针：

   • l1 = m - 1：指向 nums1 的最后一个有效元素。

   • l2 = n - 1：指向 nums2 的最后一个元素。

   • l3 = m + n - 1：指向 nums1 的末尾（合并后的位置）。

2. 逆向遍历合并：

   • 比较 nums1[l1] 和 nums2[l2]，将较大的值放入 nums1[l3]，并移动对应指针。

   • 重复直到 nums1 或 nums2 遍历完毕。

3. 处理剩余元素：

   • 如果 nums2 有剩余元素（l2 >= 0），直接复制到 nums1 的前端。

代码：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) { int l1 = m-1,l2 = n-1,l3 = m+n-1; while(l1>=0 && l2>=0) { if(nums1[l1]>nums2[l2]) { nums1[l3] = nums1[l1]; l3--;l1--; } else { nums1[l3] = nums2[l2]; l2--;l3--; } } while(l2>=0) { nums1[l3] = nums2[l2]; l2--;l3--; }}

化工基础知识