MATLAB | 第一章-1 | 矩阵与数组的应用 | 基础学习
目录
1.1常量和变量
1.1.1常量
1.1.2变量
1.1.3变量使用规则
1.1.4全局变量
1.1.5数据类型
常用标点符号功能
数据类型转换
练习
1.2矩阵的操作
1.2.1创建矩阵的方法
1.2.2创建向量的方法
→线性等间距生成向量矩阵(start:step:end)
→线性向量 linspace(n1,n2,k)
→对数向量logsoace(n1,n2,n)
1.2.3常用特色矩阵
→全0矩阵zeros()
→全1矩阵ones()
→单位矩阵eye()
→对角矩阵diag()
练习
→矩阵对角连接:blkdiag(A,B)
→计算矩阵的特征值和特征向量eig()
→随机矩阵rand()
→伴随矩阵company(m,n)
→矩阵上下翻转flipud(A)
→矩阵左右翻转fliplr(A)
→魔方矩阵magic()
→杨辉三角矩阵pascal()
→托普利兹矩阵toplitz()
→下三角矩阵tril(A)
→上三角矩阵triu()
→稀疏矩阵Sparse(A)
→希尔伯特矩阵hilb(n)
1.2.4稀疏矩阵
→创建稀疏矩阵
练习
→创建带状稀疏矩阵
练习
→稀疏矩阵操作函数
练习
1.2.5创建素数矩阵
1.2.6对角线为奇数的矩阵
1.2.7矩阵拆分(分解)
练习1
练习2拓展矩阵
√√√√1.3矩阵的运算
1.3.1矩阵常用运算
算术运算
练习1
复数运算
练习
关系运算(返回0或1)
逻辑运算(返回0或1)
1.3.2矩阵、向量元素的和sum()与积运算prod()
矩阵、向量的和s=sum(x)
矩阵、向量的积s=prod(x)
1.3.3矩阵、向量累加和cumsum()与累乘积cumprod()
矩阵、向量的累加和s=cumsum(x)
矩阵、向量的累乘积s=cumprod(x)
1.3.4矩阵平均值与中值
→矩阵平均值mean()
→矩阵中值median()
1.3.5矩阵最大值、最小值与排序
→求向量、矩阵的最大值和最小值max()
1.3.6矩阵的秩、迹和条件数
→矩阵的秩rank(A)
→矩阵的迹trace(A)
→矩阵的条件数cond(A)
1.3.7矩阵的逆inv(A)
练习-线性方程求解
1.3.8 eig()矩阵的特征值和特征向量
练习
1.3.9矩阵的海森伯格变换
1.1常量和变量
1.1.1常量
pi:π
i或j:虚数
eps正的极小值eps=2.22×10-16
Inf:无穷大
(Inf 与-Inf)
NAN:不定量
realmin最小正实数;
realmax最大正实数
1.1.2变量
变量工作区
导入数据
保存工作区
新建变量
打开变量
清除工作区菜单
可以自己新建变量二维表,适合成批导入变量到matlab中
1.1.3变量使用规则
matlab的变量名,函数名,文件名:字母+数字+下划线(英文开头、不能有空格)
1.1.4全局变量
global
1.1.5数据类型
有符号整数:int8 int16 int32 int64
无符号整数:uint8 uint16 uint32 uint64
单精度浮点:single
双精度浮点:double
字符串类型:char
单元数组 cell
结构体类型:struct
函数句柄类型:function_handle
逻辑类型:logical
class()
判断数据类型
syms y; % 等价于 y = sym(\'y\');
常用标点符号功能
符号
名称
功能描述
示例
;
分号
1. 抑制命令窗口输出 2. 分隔矩阵的行
x = 5;A = [1 2; 3 4];
.
点号
1. 元素级运算2. 访问结构体或对象的属性 / 方法
C = A.*B; s.name = \'data\';
:
冒号
1. 创建等间距向量 2. 选择矩阵的所有行 / 列
3. 定义循环范围
x = 1:2:10;
col2 = A(:,2);
for i=1:10
()
括号
1. 函数调用参数列表 2. 数组索引
3. 改变运算优先级
y = max([1,5,3]);
A(2,:) = [5,6];
[]
方括号
1. 创建向量或矩阵
2. 合并多个变量
v = [1,2,3];
[min_val, idx] = min(v);
{}
花括号
创建或访问元胞数组
C = {1, \'text\', [2 3]};
C{2} = \'new text\';
\' \'
单引号
1. 创建字符串
2. 定义函数句柄
s = \'hello\';
f = @sin;
\" \"
双引号
创建字符串(MATLAB R2017a 及以后版本)
s = \"world\";
@
@符号
1. 创建函数句柄
2. 定义类方法
h = @sin;
function y = myfun(x)
数据类型转换
数值型→整形
int=int32(0.5) ==1
数值型→逻辑型
logic=logical(10)
数值型→字符型
str=num2str(123)
整形→数值型
num=double(int32(10))
字符型→逻辑性
logic=logical(‘tadsdf’)
字符型→数值型
num=str2double(‘123’)
练习
a1=int8(10)
b1=uint8(50)
c1=single(-90.99)
a2=int16(-20)
b2=uint16(60)
d1=double(3.14159)
a3=int32(-30)
b3=uint32(70)
f1=’hello’
a4=int64(40)
b4=uint64(80)
g1.namae=’fumingxuan’
h1=@sind
i1=true、false
j1{2,1}=100
可以用 whos查看内存变量
1.2矩阵的操作
1
2
1.2.1创建矩阵的方法
矩阵包括(实数)(复数)
A=[1 2 3;4 5 6]
B=[1+2i 2+5i;3+7i 8;9+6i 8i]
1.2.2创建向量的方法
matlab把数组或向量看出1*n或n*1的矩阵,数组、向量和二维矩阵在本质上没区别,维数都是2
→线性等间距生成向量矩阵(start:step:end)
%start为起始值,step为步长,end为终值
a=[1:3:15] → a=1 4 7 10 13
→线性向量 linspace(n1,n2,k)
%产生线性向量,其中n1为初始值,n2为终值,k为个数
b=linspace(3,18,4) → b=3 8 13 18
→对数向量logsoace(n1,n2,n)
%产生对数向量,行向量值为10n1~10n2,数据个数为n
c=logspace(1,3,3) → c=10 100 1000
1.2.3常用特色矩阵
→全0矩阵zeros()
zeros(m):m*m阶0矩阵
zeros(m,n):m*n阶0矩阵
→全1矩阵ones()
ones(m):m*m阶全1矩阵
ones (m,n):m*n阶全1矩阵
→单位矩阵eye()
eye(m):m*m阶单位矩阵
eye (m,n):m*n阶单位矩阵
左上角→右下角全为1,矩阵的秩为1
→对角矩阵diag()
以v为对角元素的对角矩阵
v=[1 2 3 4];diag(v) → 对角为v的值
diag(A)→ 提取A的对角阵值
练习
使用MATLAB,创建一个对称的矩阵,并确保其对角线上的元素为0。
a=rand(5)
b=(a+a\')/2
c=b-diag(diag(b))
先生成随机矩阵
确保矩阵对称
确保对角线元素为0
→矩阵对角连接:blkdiag(A,B)
blkdiag(A,B)
a=[1 2 3;4 5 6]; b=a; c=blkdiag(a,b)
c =
1 2 3 0 0 0
4 5 6 0 0 0
0 0 0 1 2 3
0 0 0 4 5 6
→计算矩阵的特征值和特征向量eig()
[V,E] = eig(A)
特征值构成对角阵E,V各列是相应的特征向量
d = eig(A)
计算特征值
→随机矩阵rand()
rand(m,n):m*n阶均匀分布的随机矩阵【0~1】
rand(size(A)):【0~1】区间A维均匀随机矩阵
→伴随矩阵company(m,n)
→矩阵上下翻转flipud(A)
→矩阵左右翻转fliplr(A)
→魔方矩阵magic()
magic(n):必须为n阶矩阵
指:行、列、对角线元素的和相同
→杨辉三角矩阵pascal()
pascal(阶数n)

→托普利兹矩阵toplitz()
toplitz(m,n)
指:除第1行第1列元素外,每个元素与它左上角元素相同
→下三角矩阵tril(A)
A=[1 2 3 ;4 5 6;7 8 9]
tril(A)
指:保存矩阵A上三角矩阵为原值,下三角为0的矩阵
→上三角矩阵triu()
triu(A,k)
指:将矩阵A的第k条对角线以上的元素变成上三角矩阵
→稀疏矩阵Sparse(A)
→希尔伯特矩阵hilb(n)
n阶希尔伯特矩阵(关于对角线对称)
1.2.4稀疏矩阵
定义:若矩阵中非0元素个数远小于矩阵元素总值,切非0元素分布没有规律
→创建稀疏矩阵
s=sparse(A)
将矩阵A中任何0元素去除,非0元素组成矩阵
s=sparse(i,j,s,m,n,maxn)
由向量i j s生成一个m*n含有maxn非0元素的稀疏矩阵,并且有s(i(k),j(k))=s(k)
练习
i=[2 2 3 3 3 4],j=[2 4 3 2 1 4],A=[2 3 7 1 4 6],创建稀疏矩阵
i=[2 2 3 3 3 1];
j=[2 4 3 2 1 4];
A=[2 3 7 1 4 6];
s=sparse(i,j,A,4,4)
d=full(s)
s = (3,1) 4
(2,2) 2
(3,2) 1
(3,3) 7
(1,4) 6
(2,4) 3
d =
0 0 0 6
0 2 0 3
4 1 7 0
0 0 0 0
→创建带状稀疏矩阵
s=spdiags(A,d,m,n)
生成m*n所有元素,非0元素在对角线上,对角线元素有规律
A:全元素矩阵;d:指定s矩阵对角线位置,mn为行列数
练习
A=rand(5)
a=floor(10*A)
先将随机矩阵 A 的每个元素乘以 10,再通过 floor 函数向下取整。这样得到的矩阵 a 中的元素都是 0 到 9 之间的整数。
s=spdiags(a,所在矩阵左下角-所在矩阵右上角【中间为0】,5,5)
%%%%s=apdiags(a,[0,1]【代表一个便宜0,一个偏移1,两个对角矩阵】,5,5)
full(s)
→稀疏矩阵操作函数
nnz(s)
查看非0元素个数
nonzeros(s)
获取非0元素值
nzmax(s)
获取存储非0元素的空间长度
spy(s)
稀疏矩阵非0元素的图形表示
练习
A=rand(5); a=floor(10*A); s=spdiags(a,[0 2],5,5); s1=full(s)
a=nnz(s1) b=nonzeros(s1) c=nzmax(s1) spy(s)
1.2.5创建素数矩阵
素数判断函数
isprime(c)
matrix = zeros(3);
for i = 1:3
for j = 1:3
num = randi([1, 100]);
if isprime(num)
matrix(i, j) = num;
end
end
end
1.2.6对角线为奇数的矩阵
eye()+diag()
A = eye(3);
B = diag([1 3 5]);
c=A*B
1.2.7矩阵拆分(分解)
定义:将一个复杂矩阵拆分成多个较简单的矩阵,按照给定的行列索引提取元素
A(m,n)
提取矩阵A第m行,第n列元素
A(:,n)
提取矩阵A第n列元素
A(m1:m2,n1:n2)
提取矩阵A第m1行-m2行和n1列-n2列元素
A(m,:)
提取矩阵A第m行元素
A(:)
矩阵按列元素输出
矩阵拓展:如果在矩阵中赋值给1个不存在的地址,则该矩阵会自动扩展行、列数,并在该位置上添加这个数
练习1
A=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18]
a=A(2,:)
c=A(1:3,2:4)
练习2拓展矩阵
A=[1 2 3;4 5 6]
A(3,4)=20
√√√√1.3矩阵的运算
1
2
前三年课程成绩+比赛加分:专业第二
1.3.1矩阵常用运算
算术
复数
关系
逻辑
算术运算
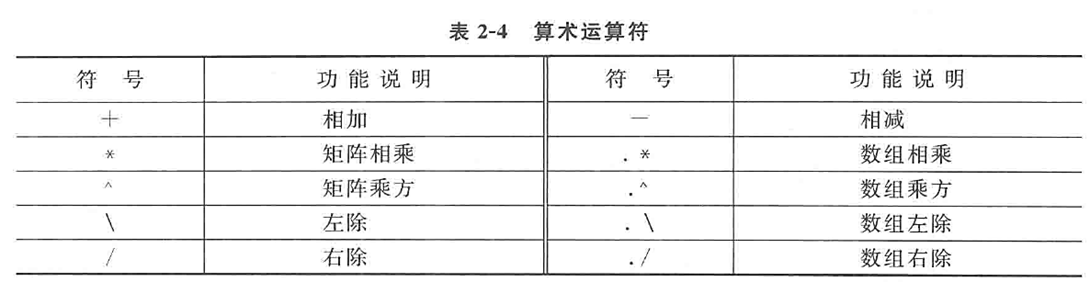
\\左除
A*X=B时→解为X=A\\B
/右除
X*A=B时→解为X=B/A
- .^(点乘方)是元素级运算,用于对数组中的每个元素单独进行乘方操作。
- ^(乘方)是矩阵运算,要求操作数满足矩阵乘法规则(如方阵才能进行乘方)
练习1
根据3*3魔方矩阵A的值,计算A*A,A2与A.^2
A=magic(3)
a=A*A
B=A^2
C=A.^2
.^2:各个元素平方
^2:矩阵*矩阵
复数运算
练习
已知复数z1=3+4i, z2=1+2i; z3=2eπi/6
计算z=z1*z2/z3
关系运算(返回0或1)

y=[1 2 3]>2 → y=0 0 1
逻辑运算(返回0或1)
& 与
| 或
~ 非
x=[true false true] → x=1 0 1
1.3.2矩阵、向量元素的和sum()与积运算prod()
矩阵、向量的和s=sum(x)
s=sum(x)
x为向量,返回元素和;
x为矩阵,返回列向量和(也是向量)
矩阵、向量的积s=prod(x)
s=prod(x)
x为向量,返回元素积;
x为矩阵,返回列向量积(也是向量)
1.3.3矩阵、向量累加和cumsum()与累乘积cumprod()
矩阵、向量的累加和s=cumsum(x)
s=cumsum(x)
方式与上述相同,不同为累加,前面所有元素+本身
矩阵、向量的累乘积s=cumprod(x)
s=cumprod(x)
方式与上述相同,不同为累积,前面一个元素*本身
1.3.4矩阵平均值与中值
→矩阵平均值mean()
mean(x)
x为向量,返回x的 算术平均值;
x为矩阵,返回x的列向量 算术平均值
mean(x,dim)
dim为1时:返回 “列向量”平均值 值为行向量
dim为2时:返回 “行向量”平均值 值为列向量
→矩阵中值median()
median(x)
median(x, dim)
x为向量,返回x的 中值;
x为矩阵,返回x的列向量 中值
1.3.5矩阵最大值、最小值与排序
→求向量、矩阵的最大值和最小值max()
Y=max(A)
向量:返回最大值,【包含复数,则按模数取】
矩阵:返回矩阵每列最大值
[Y,I]=max(A)
Y为最大值,I为最大值序号
【包含复数,则按模数取】用法同上
Y=max(A,[],dim)
Y为最大值,dim:模数
dim=1:向量直接取最大值;矩阵返回每列最大
dim=2:向量直接取最大值;矩阵返回每行最大
最小值使用方式相同
matrix = [1 2 3; 4 5 6; 7 8 9]
[m,n]=max(matrix)
fprintf(\'最大值:%d %d %d,位置:%d %d %d\',m,n)
→矩阵的排序sort()、sortrows()
sort(A)
向量、数组:按照默认升序排
矩阵:对每一列按照默认升序排
Y=sort(A,dim,‘mode’)
dim=1:列排序
dim=2:行排序
mode=ascend 升序
mode=descend 降序
sortrows() 可以使用选定的列值进对矩阵进行排序
[Y,I]=sortrows(A,Column)
Y:排列后的矩阵
I:排序后的行在之前矩阵中的行标值(显示原来顺序)
Column:列的序号,指定按照哪一列(值大小)排序
【正:升序】 【负:降序】
1.3.6矩阵的秩、迹和条件数
→矩阵的秩rank(A)
→矩阵的迹trace(A)
定义:矩阵对角线之和(左上→右下)
→矩阵的条件数cond(A)
1.3.7矩阵的逆inv(A)
定义:若A·B=B ·A=E,则称A和B为互逆矩阵
inv(A)
练习-线性方程求解
求解线性方程组的解
{2x+3y+5z=5
x+4y+8z=-1
x+3y+27z=6}
A=[2 3 5;1 4 8;1 3 27]
b=[5;-1;6] %或者b=[5 -1 6]’
j=inv(A)*b %类似Ax=B,则x=A-1B
h=A\\b
1.3.8 eig()矩阵的特征值和特征向量
γx=Ax
则γ为矩阵A的一个特征值
x为特征值γ的一个特征向量
E=eig(A):求矩阵A的全部特征值,构成向量E
[特征向量 特征值]=eig(A):
求矩阵A的全部特征值,构成对角阵d,并求A的特征向量构成v的列向量
练习
利用a矩阵构成对角阵d,并求a的特征向量构成的列向量v
a=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16];
[v d]=eig(a)
1.3.9矩阵的海森伯格变换
定义:一个矩阵的次对角元【对线线下面一行】以下所有元素=0
H=hess(A)
求矩阵A的海森伯格转换矩阵
[P H]=hess(A)
H为矩阵A的海森伯格转换矩阵,P为满足PHP’,且P’P=I的矩阵


