网站导航
> 技术文档 > 【A题成品论文】2025华数杯数学建模A题成品论文+可运行代码参考（无偿分享）_dmf对环丁砜的溶解度

【A题成品论文】2025华数杯数学建模A题成品论文+可运行代码参考（无偿分享）_dmf对环丁砜的溶解度

网友: 技术文档 2025-09-02 19:15:40

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

多孔膜孔面积占比的机理建模与制备工艺优化研究

摘要

本文围绕多孔膜光反射性能中孔面积占比的优化与控制，系统构建了基于物理机理的数学模型，并结合统计分析及数值优化方法，深入探讨了关键工艺参数对孔面积占比的影响，形成了完整且递进的解决方案。

针对问题一：本问建立了DMF溶剂蒸发过程的机理模型，依据质量守恒和扩散动力学原理，详细描述了溶剂蒸发与质量传递过程，定量分析了制备过程中关键变量的变化规律，为后续孔面积占比的机理建模奠定了基础。

针对问题二：基于问题一的机理模型，结合实验数据，采用非线性最小二乘法对孔面积占比与温度、湿度、固含量之间的非线性关系进行拟合，建立了多项式响应面模型。该模型准确反映了各变量间的非线性及交互效应，实现了孔面积占比的精确预测。

针对问题三：以问题二的多项式模型为基础，采用带约束的L-BFGS-B数值优化算法，结合解析梯度求解了约束范围内使孔面积占比最大的制备参数组合。多起点初始化策略保证了求解的全局最优性。

针对问题四：基于附件数据，开展了对多孔膜孔面积占比影响因素的统计分析，揭示了关键工艺变量及其耦合效应。随后，在保留问题三优化框架的基础上，针对统计结果对机理模型进行了改进，重新建立了包含高阶项及交互作用的多项式模型，并重新进行最优制备参数的求解。模型拟合度和预测性能均优于前述模型，验证了影响因素分析对机理模型完善的重要作用。

综上所述，本文通过四个问题的逐步深入研究，结合机理建模、非线性拟合、约束优化与统计分析，系统解决了多孔膜孔面积占比的机理描述与最优制备问题。研究方法与结果紧密衔接，构建了科学、严谨且可推广的多孔膜制备参数优化方案，为实际工艺改进提供了坚实的理论支撑。

关键词： 多孔膜；孔面积占比；机理模型；非线性最小二乘法；L-BFGS-B优化

  • 问题重述
    1. 问题背景

多孔膜作为一种重要的功能材料，在过滤、分离、催化以及光学调控等地方具有广泛应用。其内部结构的微观孔隙特征直接决定了材料的性能表现，尤其是孔面积占比对光反射和透射特性产生关键影响[1]。多孔膜的制备工艺复杂，受环境温度、湿度、溶液成分等多种因素的共同作用，导致孔隙结构在形成过程中呈现出高度的动态变化和非均匀性[3]。准确理解这些因素如何影响孔隙的形成与分布，对于实现多孔膜性能的精细调控至关重要。

此外，多孔膜材料在实际应用中常面临环境条件波动和工艺参数不稳定的挑战，这对其结构稳定性和功能可靠性提出了更高要求[5]。随着新型材料和纳米技术的发展，如何通过合理控制制备条件，实现多孔膜光学性能的优化，成为材料科学和工程领域的研究热点[4]。研究多孔膜孔结构与光反射性能的关系，不仅有助于推动相关应用技术的进步，也对促进绿色环保、高效能分离技术的发展具有重要意义[2]。

    1. 问题提出

考虑到问题陈述中确定的背景信息和限制条件，我们需要解决以下问题：

问题一：建立DMF溶剂蒸发过程的机理模型，描述制备过程中溶剂的蒸发及质量变化规律。

问题二：基于第一问的机理模型，利用实验数据拟合孔面积占比与温度、湿度和固含量之间的非线性关系，建立相应的多项式响应模型。

问题三：应用带约束的数值优化算法，求解使孔面积占比最大化的最优制备参数组合，包括温度、湿度和固含量。

问题四：在问题三的基础上，利用附件数据开展影响因素分析，重构机理模型，重新求解最优制备条件，并与问题三的结果进行比较。

  • 问题分析

问题一：本问聚焦于DMF溶剂的蒸发过程机理，旨在通过建立质量守恒和扩散动力学模型，定量描述溶剂在制备过程中的迁移与蒸发规律，揭示工艺参数对膜结构形成的基础影响机制。

问题二：基于问题一建立的机理模型，结合实验数据，采用非线性最小二乘法对孔面积占比与温度、湿度及固含量之间的复杂非线性关系进行拟合，旨在构建精确的多项式响应面模型，反映变量间的交互效应和非线性特征。

问题三：在第二问拟合模型基础上，利用带边界约束的L-BFGS-B数值优化算法，针对实际工艺参数范围，求解孔面积占比的最大化问题，实现多孔膜制备条件的最优配置，保证求解结果的全局最优性与物理合理性。

问题四：通过对附件数据的深入统计分析，识别多孔膜孔面积占比的关键影响因素及其耦合效应，在保留问题三优化框架的基础上，改进机理模型结构，加入更高阶及交互项，重新进行数值优化，提升模型拟合精度及预测性能，并与第三问结果进行系统对比分析。

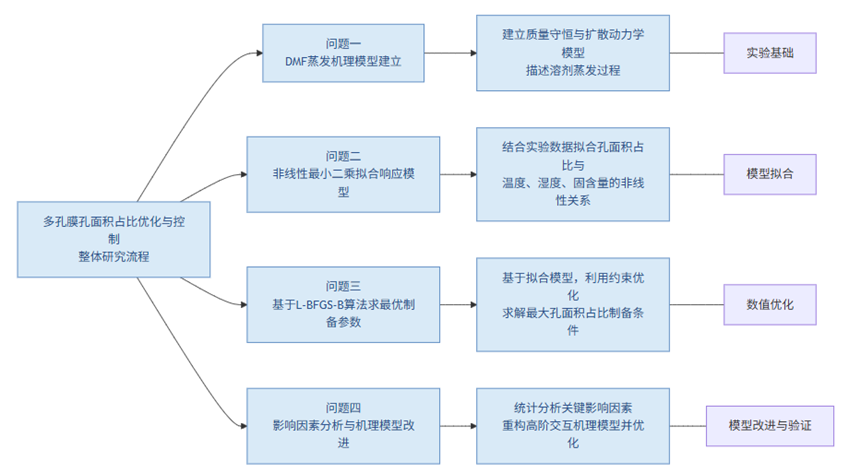
图 1 多孔膜孔面积占比优化与控制的整体研究框架

以上流程图1系统展示了多孔膜孔面积占比优化与控制的整体研究框架。图中自左向右依次为四个关键问题的研究内容：问题一通过建立DMF溶剂蒸发机理模型，揭示溶剂在制备过程中的传质规律；问题二基于实验数据，采用非线性最小二乘法拟合孔面积占比与工艺参数间的复杂关系；问题三利用带约束的数值优化方法，求解最大化孔面积占比的最优制备参数；问题四则在统计影响因素分析的基础上，重构更为精细的机理模型并重新优化，提升模型的预测准确性和适用性。整个流程结构严谨，环环相扣，体现了从基础机理到模型优化的递进研究思路。

  • 模型假设与符号说明
    1. 模型基本假设
  1. 多孔膜制备过程中的DMF溶剂蒸发遵循质量守恒和扩散动力学规律，且溶剂蒸发速率可视为时间和环境条件的连续函数。
  2. 温度、湿度和固含量是影响孔面积占比的主要工艺参数，其他环境因素或参数对孔面积占比的影响较小，可以忽略。
  3. 孔面积占比与温度、湿度及固含量之间存在非线性及交互关系，且该关系可用有限阶多项式模型有效近似。
  4. 机理模型中的各变量满足实验测定的上下界限制，且变量之间相互独立，不存在变量测量误差的相关性。
  5. 优化求解过程中，孔面积占比关于工艺参数的响应面连续且可导，适用于基于梯度的数值优化算法（如L-BFGS-B）。
  6. 所有实验数据具有代表性，且满足统计分析和拟合模型的基本假设，包括误差独立同分布、残差正态性等。
    1. 符号说明

  • 四、多孔膜孔面积占比的理论模型构建

随着对高效辐射降温材料的研究不断深入，通过调控微结构来提升材料光反射性能成为重要方向。醋酸纤维素多孔膜作为一种具有广泛应用前景的新型材料，其反射性能直接受到孔结构分布的影响，特别是孔面积占比被视为反射能力的关键控制因子。

根据制备工艺描述，多孔膜的孔结构形成过程可分解为五个核心阶段，分别为：N,N-二甲基甲酰胺（DMF）溶剂的蒸发、非溶剂环丁砜与醋酸纤维素的析出、析出液滴的布朗运动、小液滴之间的碰撞合并，以及大液滴进一步吸收小液滴后的增大过程。最终，环丁砜液滴在膜结构固化后形成孔洞，其中大液滴所形成的大孔成为孔面积占比的主要来源。

本问题的核心目标在于，通过机理建模方式，构建一个能够从制备条件（如温度 T、环境湿度 H、固含量 S_C）出发，准确描述孔面积占比A的理论数学模型A = f(T, H, S_C, \\mathbf{k})。该模型将成为后续参数反演与优化控制的基础，具有高度的理论价值与工程应用指导意义。

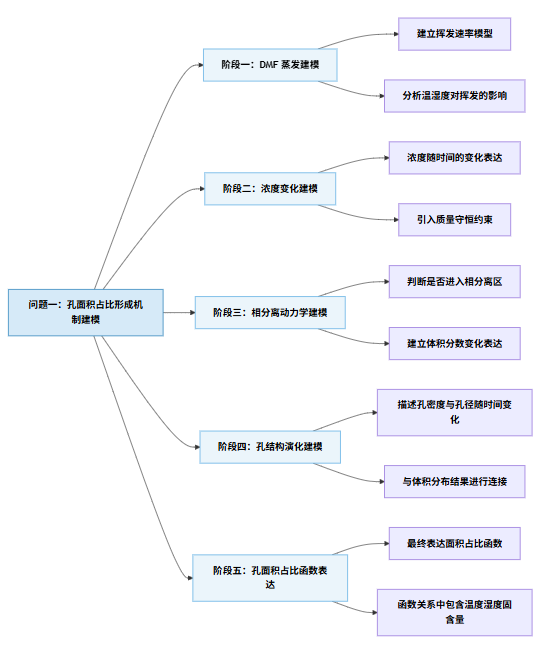
图2流程框架图

图2展示了孔面积占比形成机制的五阶段建模路径，从溶剂挥发到相分离及孔结构演化，逐步建立起孔面积占比与关键控制参数（温度、湿度、固含量）之间的关系。

    1. 蒸发动力学模型构建与分析

在多孔膜的制备过程中，DMF 的蒸发速度直接影响体系中溶剂质量的变化，进而影响非溶剂与聚合物的析出速率与液滴形成时机。为刻画蒸发过程的演化规律，设 m_D(t) 表示时间 t 时刻溶剂 DMF 的质量，蒸发速度为 v_{\\text{vap}}，则其质量变化满足基本守恒关系：

\\frac{dm_D}{dt} = -v_{\\text{vap}}

实验与文献表明，DMF 的蒸发速率与其在混合溶液中的体积分数、环境温度、饱和蒸气压以及空气湿度密切相关。为建立数学表达式，考虑以下模型结构：

v_{\\text{vap}} = k_1 \\cdot (1 - k_h H) \\cdot \\frac{P_{\\text{sat}}(T)}{V_{\\text{sol}}}

其中，k_1 为比例系数，k_h \\in [0,1]表示空气湿度对蒸发速率的抑制强度，P_{\\text{sat}}(T)表示在温度 T 下的饱和蒸气压，V_{\\text{sol}} 为溶液体积。依据 Antoine 方程，可表示饱和蒸气压为：

\\log_{10} P_{\\text{sat}} = A - \\frac{B}{C + T}

其中A, B, C为物质特定常数（可查表获取）。该模型有效整合了温度与湿度两个主控因素的影响，为后续析出模型提供基础性输入变量。

    1. 非溶剂析出与质量守恒建模

DMF 作为主要溶剂，其蒸发导致体系中溶解能力下降，从而触发环丁砜与醋酸纤维素的析出过程。析出物质的数量决定了后续液滴形成的潜能，因此对其进行质量守恒分析具有基础性意义。

记SS为 DMF 对环丁砜的饱和溶解度，SC为对醋酸纤维素的饱和溶解度。设体系中分别投料的质量为 m_S(t) 与 m_C(t)，当前 DMF 质量为 m_D(t)。当任意物质的实际质量超过 DMF 的最大溶解量时，其超出部分即发生析出，模型表达如下：

  • 若 SS \\cdot m_D(t)\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?m_S%28t%29%20%3E%20SS%20%5Ccdot%20m_D%28t%29\" />，则环丁砜的析出质量为：

m_{S,\\text{out}}(t) = m_S(t) - SS \\cdot m_D(t)

  • 若 SC \\cdot m_D(t)\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?m_C%28t%29%20%3E%20SC%20%5Ccdot%20m_D%28t%29\" />，则纤维素的析出质量为：

m_{C,\\text{out}}(t) = m_C(t) - SC \\cdot m_D(t)

该模型捕捉了体系从稳定溶解态向相分离态转变的关键点，并为后续的扩散与碰撞建模提供源项基础。

    1. 布朗运动与扩散行为建模

析出的环丁砜形成小液滴，悬浮于溶液中，在分子热运动驱动下发生无规则布朗运动。布朗运动的扩散速度直接决定了液滴间的平均碰撞频率，是形成大液滴的前驱过程。

扩散系数由斯托克斯-爱因斯坦方程表示为：

D = \\frac{k_B T}{6 \\pi \\eta r}

其中 k_B 为玻尔兹曼常数，T 为热力学温度，\\eta 为溶液黏度，r 为液滴半径。溶液黏度受非溶质影响显著，依据爱因斯坦黏度模型：

\\eta = \\eta_0 (1 + 2.5 \\phi_C)

\\phi_C = \\frac{m_{C,\\text{out}} / \\rho_C}{V_{\\text{sol}}}

其中\\rho_C为醋酸纤维素密度，\\eta_0 为纯溶剂黏度。扩散速度控制了单位时间内液滴迁移的空间范围，进一步影响碰撞强度。

为简化布朗粒子的随机路径分析，设其平均速度与扩散系数成正比：

v_d \\propto \\sqrt{D} \\propto \\sqrt{\\frac{T}{\\eta}}

该表达式为碰撞速率计算提供运动因子，体现了温度升高促进液滴运动，析出物增加则因提高黏度抑制运动的双重作用。m_{S,\\text{out}}

    1. 液滴碰撞模型构建与演化分析

环丁砜小液滴在布朗运动作用下随机移动，彼此之间在空间中发生碰撞与合并，形成大液滴。这一过程为大孔结构的初始来源，需建立碰撞频率模型。

设小液滴数密度为 n，平均半径为 r，平均速度为 v_d，两液滴间碰撞频率为：

Z = 2 \\pi r^2 v_d n

由质量守恒，n 与析出环丁砜质量 m_{S,\\text{out}} 及液滴体积 v 成正比：

n = \\frac{m_{S,\\text{out}}}{\\frac{4}{3} \\pi r^3 \\rho_S}

单位时间内形成的大液滴质量 m_{\\text{gen}} 与碰撞频率成正比：

m_{\\text{gen}} \\propto Z \\cdot m_{S,\\text{out}} \\propto r^2 v_d n \\cdot m_{S,\\text{out}}

代入 n 的表达式后，该关系式成为温度、析出质量、液滴尺寸与黏度等参数的函数，反映制备条件对结构形成效率的控制作用。

    1. 大液滴增大模型构建与吸收机制

已形成的大液滴可进一步通过吸收运动中的小液滴而增大，最终形成可计入孔面积的大孔洞。考虑到液滴之间体积差异显著，可将小液滴视作点粒子，大液滴视为近似静止的界面，采用几何碰撞模型描述吸收过程。

假设小液滴速度为 v_d，其与大液滴表面法线方向上的分量为v_{\\perp} = v_d \\cos \\theta。设大液滴总表面积为 S，则单位时间内撞击大液滴的小液滴数量为：

N_{\\text{hit}} \\propto S \\cdot v_{\\perp} \\cdot n \\propto S \\cdot v_d \\cdot c

其中 c 为小液滴浓度，n \\propto c。大液滴质量增长速率可表示为：

\\frac{dm_{\\text{grow}}}{dt} = k_2 \\cdot v_d \\cdot c \\cdot S

进一步假设大液滴表面积与质量之间的关系为 S \\propto m_{\\text{grow}}^{2/3}，则：

\\frac{dm_{\\text{grow}}}{dt} \\propto v_d \\cdot c \\cdot m_{\\text{grow}}^{2/3}

该式构成一个非线性常微分方程，反映液滴成长的自催化特征，可数值求解得到 m_{\\text{grow}}(t)。

    1. 孔面积占比理论模型表达式

将前述所有机制耦合考虑，在蒸发阶段结束时间t_{\\text{end}}时，大液滴的总质量与最终形成的孔面积占比 A 之间建立比例关系：

A = \\alpha \\cdot m_{\\text{grow}}(t_{\\text{end}})

结合各阶段子模型构建完整函数表达：

A = f(T, H, S_C, \\mathbf{k})

其中\\mathbf{k} = {k_1, k_h, k_2, \\eta_0, \\alpha, SS, SC, r}是所有过程中的待定系数集合。该模型具备良好的物理基础、理论连续性与参数可控性，可为后续数据拟合与实验指导提供有力工具。

  • 理论模型参数识别与应用模型构建

在第一问中，我们基于膜材料微观形成机制，从五个关键物理过程出发，建立了一个覆盖DMF蒸发、非溶剂与聚合物析出、液滴扩散布朗运动、小液滴碰撞合并以及大液滴吸收增长的综合性理论模型。该模型从机理层面揭示了制备条件与孔结构之间的定量因果链条，其最终目标是用函数形式表达如下：

A = f(T, H, S_C; \\mathbf{k})

其中 A 表示孔面积占比，T 为制备温度，H 为环境湿度，S_C为溶液初始固含量，\\mathbf{k}为多个过程性待定物理参数组成的向量。

本问题旨在基于附件2所给出的真实实验样本数据，对理论模型中涉及的多个待定参数 \\mathbf{k} 进行合理估计，构建具备数值可操作性的应用级预测模型，进而判断该理论结构在实际样本上的拟合能力与理论合理性是否一致。

后续都在“数模加油站”......

网络标签：

相关问题