2025牛客多校第十场 K.神奇集合 F.老师和Yuuka逛商场 E.老师与好感度 I.矩阵 个人题解

I.矩阵

#数学 #贪心 #构造

题目

思路

首先考虑有数最受条件的约束，因此尝试令数$x$沿着某方向前进$x$后回到原地：
( x + x + 1 ) % n − 1 = x ( 2 x + 1 ) % n = x + 1 2 x + 1 ≡ x + 1 m o d    n x ≡ 0 m o d    n \\begin{align} (x+x+1)\\%n-1&=x\\\\ \\\\ (2x+1)\\%n&=x+1\\\\ \\\\ 2x+1&\\equiv x+1\\mod n\\\\ \\\\ x&\\equiv 0\\mod n \\end{align} (x+x+1)%n−1(2x+1)%n2x+1x​=x=x+1≡x+1modn≡0modn​​
则有$x$为$n$的因数

因此，当$x$为$n$的因数时，$x$无法在$n$方向上进行移动，$m$方向同理

因此，$x=lcm(n,m)$时，$x$一定无法移动
因此$lcm(n,m)$必须为最后一个填入的数字，可以利用这一点进行$YES/NO$的判断

接下来通过观察贪心地进行填空：

• 尝试将一列填满后再填下一列
• 尝试每填完一个数就变换一次移动方向，比如这次在列方向上向下移动，下一次列方向上的移动就向上，这样可以保证移动后不会踩到已经被填过的格子

代码实现

代码由$phaethon90$书写

#include#includeusing namespace std;#define ll long long#define endl \'\\n\'ll gcd(ll a,ll b){ if(b==0) return a; else return gcd(b,a%b);}void eachT(){ ll n,m; cin>>n>>m; if(n/gcd(n,m)*m<n*m) { cout<<\"NO\\n\"; return; } vector<vector<int>>mp(n+1,vector<int>(m+1,0)); int i=0,j=0,cnt=0; int dirn=1,dirm=1; mp[0][0] = ++cnt; while(cnt<n*m) { if(cnt%n==0) { j = (j+cnt%m*dirm+m*m)%m; mp[i][j] = ++cnt; dirm *= -1; } else { i = (i+cnt%n*dirn+n*n)%n; mp[i][j] = ++cnt; dirn *= -1; } } cout<<\"YES\\n\"; for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { cout<<mp[i][j]<<\' \'; } cout<<endl; }}int main(){ ios::sync_with_stdio(0); cin.tie(0),cout.tie(0); int t=1; // cin>>t; while(t--) eachT(); return 0;}

E. 老师与好感度

#dp #线性dp

题目

思路

由于 0≤ a i ≤100 0\\leq a_{i}\\leq 100 0≤ai​≤100，很容易想到要枚举最后出现的$m$个数，考虑$m=2$的情况，即枚举两个目标 ta r 1 ,ta r 2 tar_{1},tar_{2} tar1​,tar2​（$target$）

状态表示：
$dp[i][j]$表示从$1$遍历到$i$，第$i$个学生的好感度变为 ta r j tar_{j} tarj​（$1\le j\le 2$）的最小总天数

状态转移：
d p [ i ] [ j ] =min ⁡ 0 ≤ k ≤ [ m = 2 ] { d p [ i ] [ j ]   ,   d p [ i − 1 ] [ k ] + max ⁡ { t a r j − a i − ( t a r k − a i − 1 )   ,   0 } } , 0 ≤ j ≤ [ m = 2 ] i f ( t a r j − a i < 0 ) d p [ i ] [ j ] = i n f \\begin{align} &dp[i][j]=\\min_{0\\leq k\\leq[m=2]}\\{dp[i][j]\\ , \\ dp[i-1][k]+ \\max\\{ tar_{j}-a_{i}-(tar_{k}-a_{i-1})\\ ,\\ 0 \\} \\},0\\leq j\\leq[m=2]\\\\ \\\\ &if(tar_{j}-a_{i}<0)dp[i][j]=inf \\end{align} ​dp[i][j]=0≤k≤[m=2]min​{dp[i][j] , dp[i−1][k]+max{tarj​−ai​−(tark​−ai−1​) , 0}},0≤j≤[m=2]if(tarj​−ai​<0)dp[i][j]=inf​​
当$m=2$的时候，$dp[i][j]$将由$i-1$时的两个状态转移过来，分别是选 ta r 1 ,ta r 2 tar_{1},tar_{2} tar1​,tar2​的状态
要与$0$取$max$是因为 a i a_{i} ai​与$tar$的差距可能比较小，仅用之前的天数就可以达到目标

枚举 ta r 1 ,ta r 2 tar_{1},tar_{2} tar1​,tar2​，每次都取全局最小值即可

注意， ta r 1 tar_{1} tar1​的上下界分别为 a i a_{i} ai​的最大值与最小值， ta r 2 tar_{2} tar2​的上下界分别为$200$与 ta r 1 tar_{1} tar1​

ta r 2 tar_{2} tar2​的上界不是 a i a_{i} ai​的最大值，因为可能会有区间覆盖在 a i a_{i} ai​最大值上使得它变大
最坏情况下， a i a_{i} ai​的最大值被覆盖的次数量级为$o(n)$，因此上界设为$100+100$即可

代码实现

#include#include#include#include#includeusing namespace std;using ll = long long;#define rep(i, a, b) for(int i = (a); i <= (b); i ++)#define per(i, a, b) for(int i = (a); i >= (b); i --)#define see(stl) for(auto&ele:stl)cout<<ele<<\" \"; cout<<\'\\n\';constexpr int inf = 1e9 + 5;// #define int ll const int up=155;void chmin(int&x,int y){ x=min(x,y);}void chmax(int&x,int y){ x=max(x,y);}const int N=405;int a[N],dp[N][2],t[2];void eachT() { int n,m;cin>>n>>m; int ma=0,mi=inf; rep(i,1,n){ cin>>a[i]; chmax(ma,a[i]); chmin(mi,a[i]); dp[i][0]=dp[i][1]=inf; } int ans=inf; rep(tar1,mi,ma){ rep(tar2,tar1,up){ t[0]=tar1,t[1]=tar2; dp[1][0]=t[0]-a[1]; dp[1][1]=(m==2)?t[1]-a[1]:inf;  if(dp[1][0]<0)dp[1][0]=inf; if(dp[1][1]<0)dp[1][1]=inf; rep(i,2,n){ rep(j,0,(m==2)){  rep(k,0,(m==2)){ chmin(dp[i][j],max(t[j]-a[i]-(t[k]-a[i-1]),0)+dp[i-1][k]); if(t[j]-a[i]<0)dp[i][j]=inf;  } } }  chmin(ans,min(dp[n][0],dp[n][1])); rep(i,2,n)dp[i][0]=dp[i][1]=inf; } } cout<<ans<<\'\\n\';}signed main(){ ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); ll t = 1; cin >> t; while (t--) { eachT(); }}

F. 老师和 Yuuka 逛商场

#线段树 #线段树二分

题目

思路

由于要确定两个隔板，非常容易想到的一个思路便是$o(n)$遍历左隔板，$o(\log n)$查找最优右隔板，总复杂度$o(n\log n)$

设集合 S l S_{l} Sl​表示区间$[1,l]$内的元素（去重），那么$[l+1,n]$内能对答案有贡献的数字必然要属于 S l S_{l} Sl​，因此我们可以将$[l+1,n]$这一段序列视作只剩下了属于 S l S_{l} Sl​的元素

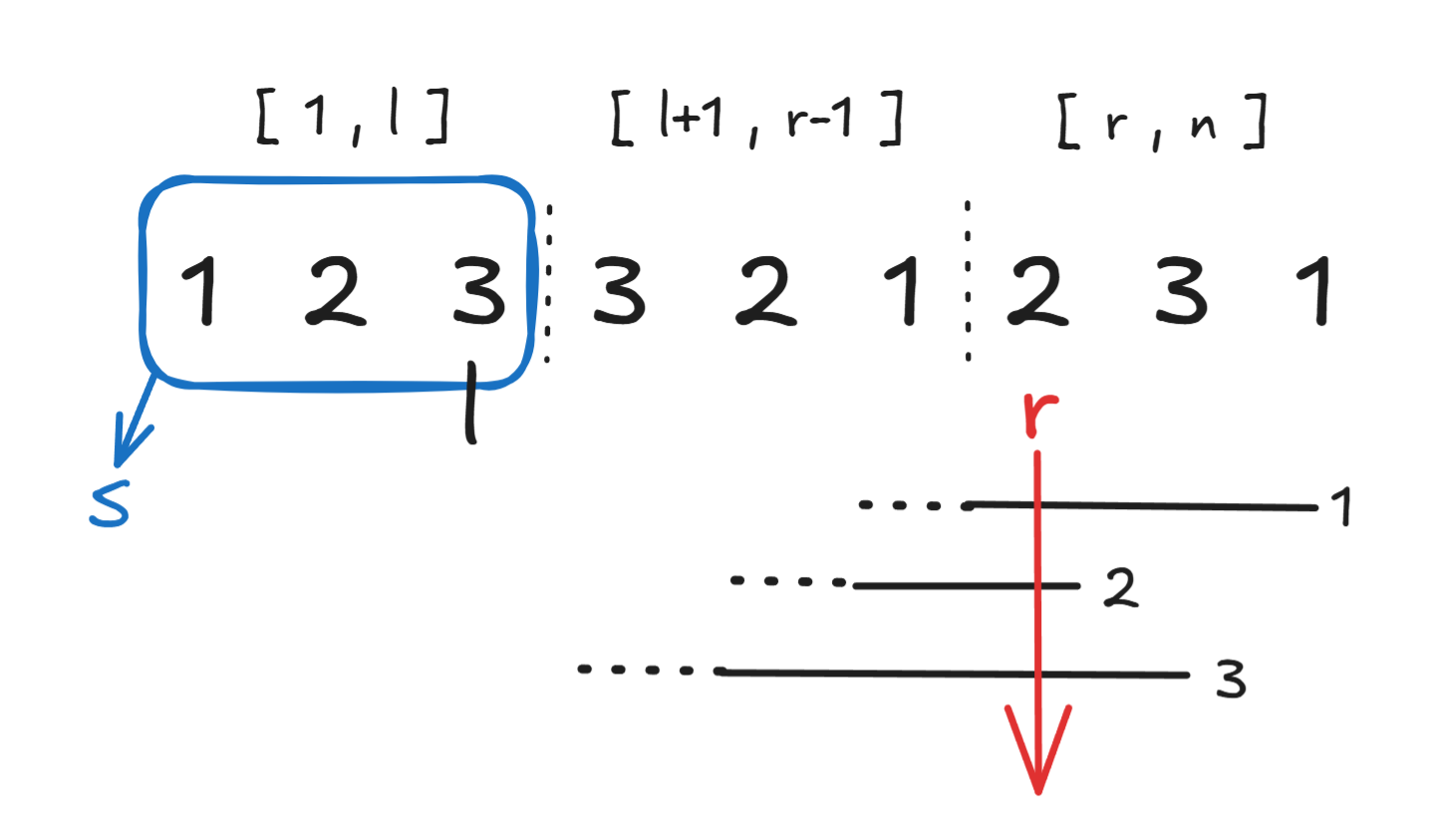
我们将序列分为三段：$[1,l],[l+1,r-1],[r,n]$
目标即使得$[l+1,r-1],[r,n]$中共同元素的数量尽可能大
因此我们对每个元素在区间$[l+1,n]$中最早出现和最晚出现的位置$lpos,rpos$进行维护，当指针落于元素$x$的$[lpos,rpos]$中时便说明该指针的左边与右边必定都有元素$x$出现

每次移动$l$指针的时候，都使用队列$deque$更新元素$a[l]$的$lpos,rpos$

接着，使用线段树对区间$[lpos+1,rpos]$进行区间$+1$，同时维护区间的最大值
为什么左端点是$lpos+1$呢？
这是为了保证指针$r$坐落于区间中的时候，$[r,n]$上必定有元素$x$，$[l+1,r-1]$上也必定有元素$x$
考虑边缘情况，若$r=lpos+1$，那么$r-1=lpos$，刚好将最左边的元素$x$包含进了区间中

令$r$指针落在区间$[l+1,n]$的$max$值的点上，此时左右区间必定有$max$值个相同元素，此处便是最优分割处

如何在线段树上找到这个$max$值的位置呢？
我们可以在线段树上二分，通过$pair$来储存$max$的值与位置：

• $pair<int,int>$类型的$find(p,l,r)$函数

  • 传回的$pair$中，$first$为$max$的值，$second$为$max$值的位置
  • 功能：查询区间$[l,r]$内的单点最大值及其位置
  • 对比左右子树的$max$值，选择$max$值较大的子树分裂查询

• $pair<int,int>$类型的$query(p,l,r,ql,qr)$函数

  • 传回的$pair$中，$first$为$max$的值，$second$为$max$值的位置
  • 功能：查询区间$[ql,qr]$内的单点最大值及其位置
  • 若$[l,r]$被$[ql,qr]$完全覆盖，那么可以直接调用$find(p,l,r)$
  • 否则需要分裂查询左子树与右子树，返回左右子树中的较大者

为什么要设计两个函数来二分查找？
因为给定的$ql,qr$不一定是某个已知线段树节点所维护的区间$l,r$，可能需要分裂成多个区间进行比较
通过$query$函数将$[ql,qr]$分裂成一个个已知区间$[l,r]$，再通过$find$函数在线段树上查找

每次更新$l$指针时，先删去$a[l]$的$[lpos+1,rpos]$，$a[l]$的$deque$进行$pop\_front$之后再加回 [lpo s ′ +1,rpos] [lpos\'+1,rpos] [lpos′+1,rpos]
调用$query(1,1,n,l+2,n)$查询区间$[l+2,n]$中的最大值与位置以确定最优的$r$指针
之所以是$l+2$的原因是，当$r$取$l+2$的时候，$r-1$为$l+1$，与之前讨论的边界情况相符

注意$l,r$分别初始化为$2,3$，以防$n=3$的情况
一直取全局最大值即可

代码实现

#include#include#include#include#include#includeusing namespace std;using ll = long long;#define rep(i, a, b) for(int i = (a); i <= (b); i ++)#define per(i, a, b) for(int i = (a); i >= (b); i --)#define see(stl) for(auto&ele:stl)cout<<ele<<\" \"; cout<<\'\\n\';constexpr int inf = 1e9;#define int ll // #define double long doubleconst int N = 1e5 + 5e4 + 5;int n, a[N];unordered_map<int, deque<int>>mp;#define ls p<<1#define rs p<<1|1#define mid ((l+r)>>1)int add[N << 2], ma[N << 2];void pushup(int p) { ma[p] = max(ma[ls], ma[rs]);}void pushdown(int p, int l, int r) { if (add[p]) { ma[ls] += add[p]; ma[rs] += add[p]; add[ls] += add[p]; add[rs] += add[p]; add[p] = 0; }}void modify(int p, int l, int r, int x, int y, int val) { if (x <= l && r <= y) { ma[p] += val; add[p] += val; return; } pushdown(p, l, r); if (x <= mid)modify(ls, l, mid, x, y, val); if (y > mid)modify(rs, mid + 1, r, x, y, val); pushup(p);}pair<int, int> find(int p, int l, int r) { if (l == r)return { ma[p],l }; pushdown(p, l, r); if (ma[ls] >= ma[rs])return find(ls, l, mid); else return find(rs, mid + 1, r);}pair<int, int> query(int p, int l, int r, int ql, int qr) { if (ql > r || qr < l) return { -1,-1 }; if (ql <= l && r <= qr) return find(p, l, r); pushdown(p, l, r); auto left = query(ls, l, mid, ql, qr); auto right = query(rs, mid + 1, r, ql, qr); return left.first >= right.first ? left : right;}void build(int p, int l, int r) { ma[p] = add[p] = 0; if (l == r)return; build(ls, l, mid); build(rs, mid + 1, r);}void eachT() { cin >> n; mp.clear(); build(1, 1, n); unordered_multiset<int>sl; rep(i, 1, n) { cin >> a[i]; mp[a[i]].push_back(i); } int ans = 0, ansl = 2, ansr = 3; rep(l, 1, n) { if (!sl.count(a[l])) { mp[a[l]].pop_front(); int posl = mp[a[l]].front(), posr = mp[a[l]].back(); if (posl + 1 <= posr)modify(1, 1, n, posl + 1, posr, 1); } else { int posl = mp[a[l]].front(), posr = mp[a[l]].back(); if (posl + 1 <= posr)modify(1, 1, n, posl + 1, posr, -1); mp[a[l]].pop_front(); if (mp[a[l]].size() >= 2) { int posl = mp[a[l]].front(), posr = mp[a[l]].back(); if (posl + 1 <= posr)modify(1, 1, n, posl + 1, posr, 1); } } sl.insert(a[l]); pair<int, int> now = query(1, 1, n, l + 2, n); if (ans < now.first) { ans = now.first; ansl = l + 1, ansr = now.second; } } cout << ans << \'\\n\' << ansl << \" \" << ansr << \'\\n\';}signed main() { ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); ll t = 1; cin >> t; while (t--) { eachT(); }}

K. 神奇集合

#强联通分量 #树上背包 #dp

题目

思路

注意到题目中添加的新边为返祖边，一旦选择了该连通块中的任意一个点，那么这整个连通块都必须要选择，因此考虑对图进行$tarjan$缩点

缩点过程中，将新点的权值、入度进行记录

由于原图是树，则添加返祖边缩点后仍然是一棵树
建好新图后遍历所有新节点，找出入度为0的点记为根节点
从根节点进入，$dfs$过程中进行树上背包dp：

状态表示：
$dp[u][j]=1/0$代表以$u$为根的子树中，是否存在总权值为$j$的神奇集合

状态转移：
s u m u ≥ i ≥ 0 , s u m s o n ≥ j ≥ 0 : d p [ u ] [ i + j ]   ∣ = d p [ u ] [ i ] & d p [ s o n ] [ j ] d p [ u ] [ s u m u ] = 1 \\begin{align} &sum_{u}\\geq i\\geq 0,sum_{son}\\geq j\\geq 0:dp[u][i+j]\\ |=dp[u][i]\\&dp[son][j]\\\\ \\\\ &dp[u][sum_{u}]=1 \\end{align} ​sumu​≥i≥0,sumson​≥j≥0:dp[u][i+j] ∣=dp[u][i]&dp[son][j]dp[u][sumu​]=1​​
从$u$节点已经遍历的所有可能权值中取出权值为$i$的情况，从$son$节点的所有可能权值中取出权值为$j$的情况，二者可以转移到$dp[u][i+j]$的状态中

最后考虑整个子树都选上的情况 dp[u][su m u ] dp[u][sum_{u}] dp[u][sumu​]

答案即为 ∑ i = 0 N dp[root][i] \\sum_{i=0}^{N} dp[root][i] ∑i=0N​dp[root][i]

代码实现

#include#include#include#include#include#include#includeusing namespace std;using ll = long long;#define int ll #define rep(i, a, b) for(int i = (a); i <= (b); i ++)#define per(i, a, b) for(int i = (a); i >= (b); i --)#define see(stl) for(auto&ele:stl)cout<<ele<<\" \"; cout<<\'\\n\';constexpr int inf = 1e9 + 5;// #include // using namespace __gnu_pbds;const int N=1e4+5;int w[N];struct node{ set<int>e; int dfn,low,in,scc;}a[N];struct node1{ set<int>e; int siz,deg,w,sum;}na[N];int tot,cnt;stack<int>st;void tarjan(int u){ a[u].dfn=a[u].low=++tot; st.push(u),a[u].in=1; for(auto&son:a[u].e){ if(!a[son].dfn){ tarjan(son); a[u].low=min(a[u].low,a[son].low); }else if(a[son].in){ a[u].low=min(a[u].low,a[son].low); } } if(a[u].dfn==a[u].low){ int v;++cnt; do{ v=st.top(),st.pop(),a[v].in=0; a[v].scc=cnt,++na[cnt].siz; na[cnt].w+=w[v]; }while(u!=v); }}int n;void build(){ rep(i,1,n){ for(auto&son:a[i].e){ if(a[i].scc!=a[son].scc){ na[a[i].scc].e.insert(a[son].scc); na[a[son].scc].deg++; } } }}bool dp[N][N];int dfs(int u,int fa){ int sum=0; dp[u][0]=1; for(auto&son:na[u].e){ if(son==fa)continue; sum+=dfs(son,u); per(i,na[u].sum,0){ per(j,na[son].sum,0){ dp[u][i+j]|=dp[u][i]&dp[son][j]; } } na[u].sum=sum; } sum+=na[u].w; na[u].sum=sum; dp[u][sum]=1; return sum;}void eachT() { cin>>n; rep(i,1,n)cin>>w[i]; rep(i,1,n-1){ int u,v;cin>>u>>v; a[u].e.insert(v); } int m;cin>>m; rep(i,1,m){ int u,v;cin>>u>>v; if(u!=v)a[u].e.insert(v); } rep(i,1,n){ if(!a[i].scc)tarjan(i); } build(); int rt; rep(i,1,cnt){ if(na[i].deg==0)rt=i; } dfs(rt,0); int cnt=0; rep(i,0,N-1)if(dp[rt][i])cnt++; cout<<cnt<<\'\\n\';}signed main(){ ios::sync_with_stdio(false); cin.tie(0), cout.tie(0); ll t = 1; // cin >> t; while (t--) { eachT(); }}