网站导航
> 技术文档 > 【论文阅读—可解释性AI(Transformer篇)】Transformer Interpretability Beyond Attention Visualization

【论文阅读—可解释性AI(Transformer篇)】Transformer Interpretability Beyond Attention Visualization

网友: 技术文档 2025-09-02 20:12:03

参考文献：CVPR 2021 Open Access Repository

摘要

Transformer 是一种非常强大的神经网络架构，最初用于处理文字，现在也越来越多地应用在图像分类任务中。我们经常想知道：模型是“看”到图像的哪些部分才做出某个判断的？为此，已有一些方法尝试使用 Transformer 的注意力图（attention maps）或基于一些规则来“追踪”模型的决策过程，参考之前博客Transformer中绘制注意力图-Attention Rollout & Attention Flow-CSDN博客。

这篇文章提出了一种全新的方法，用来解释 Transformer 是如何做出判断的：

  • 首先，它会根据一个叫做「Deep Taylor 分解」的数学原理，给每个图像区域分配一个“重要性”分数（也叫“相关性”）。

  • 然后，它将这些分数从模型的输出一步步反向传播回输入，这个过程要经过注意力层和一些跳跃连接（skip connections），而这些地方是现有方法处理起来很困难的。

  • 他们提出了一种新的计算方式，在这个传播过程中能够保持整体的重要性不变，也就是不会在传播中“丢失”解释力。

最后，作者在最新的视觉 Transformer 网络（用于图像任务）和文字分类任务上做了实验，证明他们的方法比以前的方法更清晰、更准确地解释了模型是如何做出决策的。

Introduction

Transformer是“黑箱”的，不像CNN通过卷积核提取图像特征，我们很难知道它是根据图像（或文本）的哪些部分做出判断的，如果能把模型的“思考过程”可视化，就能够为黑箱模型提供可解释性，帮助我们调试模型、检查模型是否公平没有偏见、为其他任务提供参考。

下面是Transformer的核心Self Attention（自注意力）计算机制，他会计算输入中每两个“元素”（比如词、图像小块）之间的“关注程度”，参考大模型交叉研讨课笔记-Transformer架构-CSDN博客

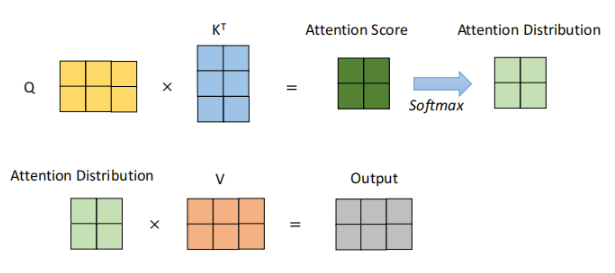
很多可视化方法就是直接用这些 attention 分数来代表模型关注了哪些部分。有的用一层，有的把多层的结果平均。但这也有问题：

  • 平均 attention 会让结果变得模糊（信息混杂在一起）

  • 每一层的作用不同，简单平均忽略了这一点

有一种叫 rollout 的方法，尝试把多层 attention 整合成一个整体的关注图，效果比单层好一些。但它有个问题：有些“无关”的区域也会被高亮显示出来，因为它基于一些过于简单的假设，具体的局限性在这篇博客里面有提到Transformer中绘制注意力图-Attention Rollout & Attention Flow-CSDN博客。

本文的方法借鉴了一种叫做“相关性传播”的思想，做了以下创新：

  • 新规则：提出了一种新的方法来传播“重要性分数”，可以处理模型中的正数和负数（因为 Transformer 中不是所有激活值都是正的）。

  • 稳定传播：专门处理了跳跃连接（skip connection）和矩阵乘法这类非参数层的传播问题，防止数值不稳定。

  • 融合信息：把 attention 信息和我们计算的 relevancy 分数结合在一起，得到更准确的可视化结果。

  • 支持多类解释：我们的方法可以解释某一个特定类别的预测，而不是一幅图就只能有一种“热力图”。

Related Work

计算机视觉中的可解释性方法（CNN为主）

在卷积神经网络（CNN）中，有很多方法可以生成“热力图”，告诉我们模型是根据图像的哪些区域做出判断的。主要有两大类方法：

梯度类方法

这些方法基于 反向传播时的梯度信息，代表模型对输入变化的敏感程度。举几个例子：

  • Gradient × Input：梯度和输入图像逐像素相乘。

  • Integrated Gradients：对输入做插值采样，计算每一步的梯度再平均，更稳定。

  • SmoothGrad：在输入图像中加噪声多次，平均这些噪声图的梯度，减少随机波动。

  • FullGrad：除了考虑输入的梯度，也考虑了偏置项（bias）的梯度。

但问题是这些方法在实际中常常是“类无关的”（class-agnostic），无论你想解释的是哪个类别，图出来的区域几乎一样。

归因传播方法

这些方法基于一个叫 Deep Taylor 分解 的理论，逐层“往回推”模型的决策过程，得到输入中哪些部分贡献最大。

  • LRP（Layer-wise Relevance Propagation）：把预测结果一步步往输入传播，要求模型中用的是 ReLU 激活函数。

但Transformer不用ReLU，因此 LRP 要改造才能用在 Transformer 上。还有一些变种方法，比如 RAP、AGF、DeepLIFT、DeepSHAP，其中：CLRP 和 SGLRP 是“类特定的”改进版，会对多个类别进行对比，从而高亮某个类别的关键区域。

其他类型的方法

  • 显著性图（Saliency methods）：基于人类感知原理找图中显眼区域。

  • 激活最大化、Excitation Backprop：用优化或反向传播找模型最关心的区域。

  • 扰动方法（Perturbation）：对输入图像局部区域进行扰动（比如遮挡），看预测结果怎么变化。这种方法直观、不需要模型细节，但计算量大。

但这些方法在Transformer上不好用，特别是文本中是离散token，不能直接做扰动。

Transformer模型的可解释性

目前专门为Transformer设计的可解释性方法还不多，主流方法大多是：使用attetnion权重本身，很多人直接把Transformer中的attention分数当做“重要性”，但这有很大局限：

  • 只用了 attention 这一部分，忽略了 key、query、value 的生成过程；

  • 忽略了其他层（比如前馈层、归一化层等）；

  • 误以为 attention 权重 = 相关性，其实并不是。

之前提出的Rollout方法的问题：

  • 假设注意力是线性组合，但实际上 attention 是非线性叠加的；

  • 没法区分正向/负向影响，即一个区域是增强了预测还是抑制了预测；

  • 简单的平均可能让无关token被误认为很重要（比如背景区域）；

  • 实验发现它会“错误地高亮”一些和预测无关的区域。

举个代码例子，Transformer中的Attetention Block如下所示：

def forward(self, x, mask=None, attn_mask=None): B, N, C = x.shape qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4) q, k, v = qkv[0], qkv[1], qkv[2] # [B, num_heads, N, D] attn = (q @ k.transpose(-2, -1)) * self.scale # [B, num_heads, D, D] attn = attn.softmax(dim=-1) attn = self.attn_drop(attn) self.attn_map = attn.detach().cpu() # 👈 存储注意力权重，避免梯度干扰 x = attn @ v x = x.transpose(1, 2).reshape(B, N, C) x = self.proj(x) x = self.proj_drop(x) return x

所以整个Transformer Attention Block的结构大致是：

Input ↓[ LayerNorm ] ↓[ Self-Attention ] ↓[ Add (残差) ] ↓[ LayerNorm ] ↓[ MLP (Linear → GELU → Linear) ] ↓[ Add (残差) ] ↓Output

Method

我们想弄清楚 Transformer 模型在做分类时到底在“看”哪里 —— 也就是每一层、每个注意力头对最终分类决策的重要程度。作者提出了一种改进的 可视化方法，它结合了 梯度（gradient） 和 相关性（relevance） 信息，来生成更准确、可解释的注意力图，特别是对某个目标类别（class-specific）。

什么是LRP

推荐一个讲解视频：https://www.youtube.com/watch?v=PDRewtcqmaI，传统的LRP是适用于CNN或MLP模型结构的，如下图传入一张图片经过CNN网络架构之后得到patch，接着前向传播得到每个类别的预测概率。LRP将网络上的输出概率作为输入，patch端的相关性的分数作为输出，构建相关性分数计算网络。

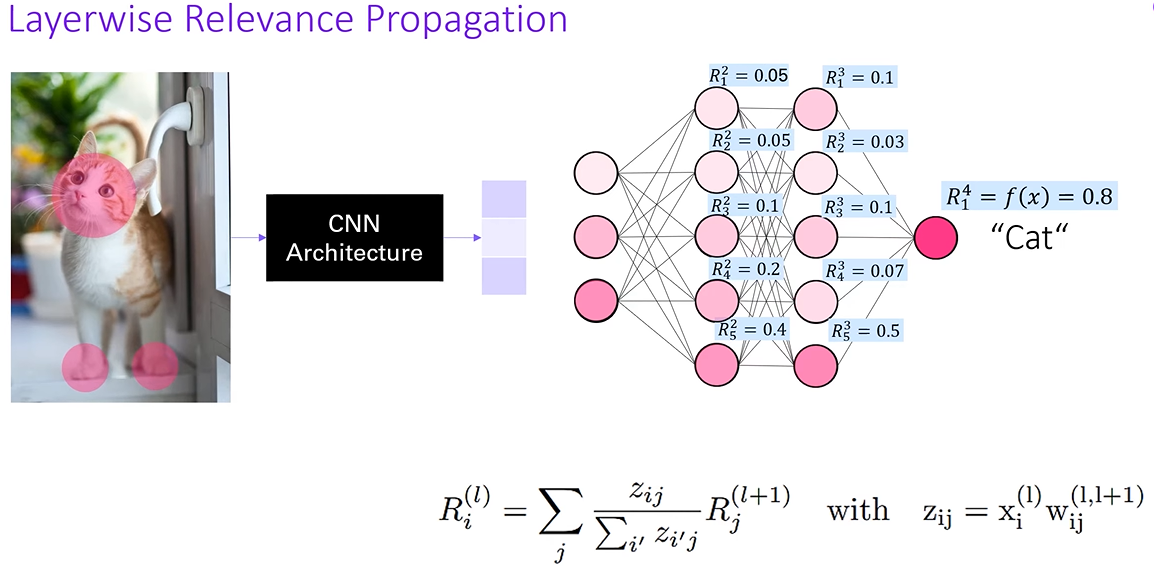
R_{1}^{4}表示第四层（输出层）的第一个节点（猫猫这个类别）的相关性分数（预测概率），接下来我们通过公式计算出下一层各个节点的相关性分数。z表示连接上下层两两节点之间的权重（贡献），z_{ij}表示的是前一层（l+1)层神经元i对当前层神经元j的贡献（注意，LRP0中不包含bias，也不经过ReLU），\\sum_{i^{\'}}z_{i\'j}表示所有上一层节点对当前节点的贡献

想象神经元j的预测结果是一个蛋糕（它的相关性是 Rj），我们想把这块蛋糕分配给它的所有“前辈”神经元i。分蛋糕的依据是：谁给它贡献多，就分得多。而这个贡献就是输入值乘以连接权重。

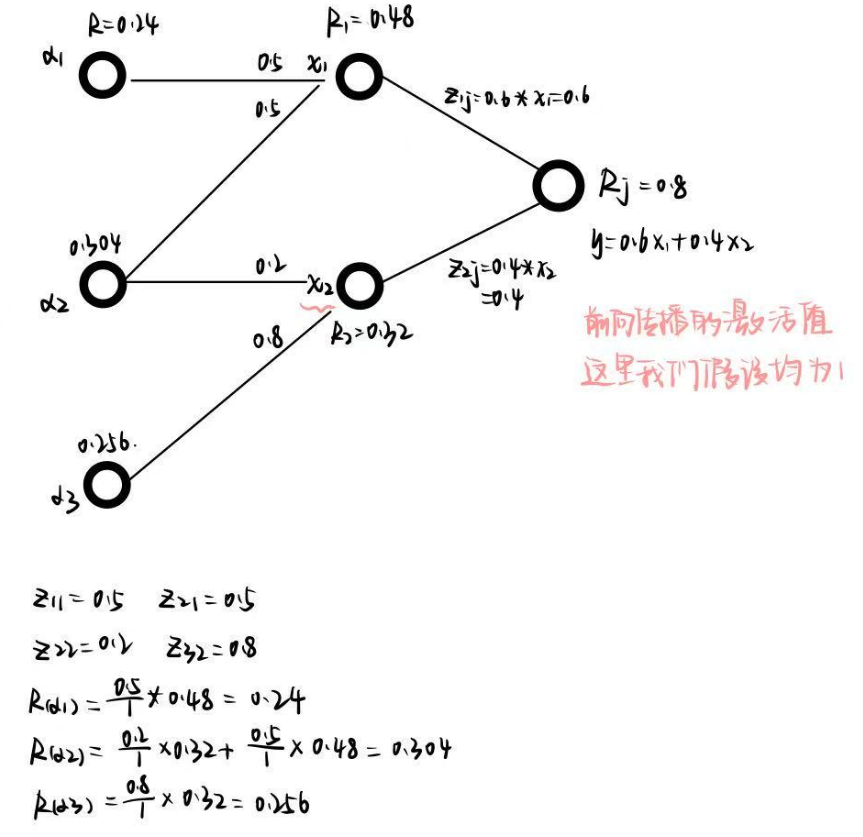
原始的LRP是保持守恒的，也就是说输出端概率为0.8，则之前的每一层相关性分数相加都是0.8。本文中为了能够让LRP适用于Transformer框架做了改进与拓展，以更好地适用于 Transformer 类模型中的自注意力结构（self-attention）。

引入了类特异性梯度和相关性传播的注意力分数计算

不仅考虑输出层预测概率，还引入了对某一目标类别的梯度和相关性分数，把梯度和LRP相关性分数进行融合。

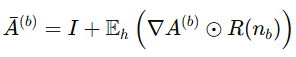
下面是根据官方代码整理出的Transformer框架中是怎么计算相关分数的，不同的层类型对应不同的相关的分数计算公式：

  • Linear：线性层中对某个节点的相关分数划分直接采用梯度，因为线性操作的梯度隐含了输入信息

  • 非线性操作（Pool,Add,Clone,Matmul）：非线性操作中梯度并不包含输入信息，所以需要乘以输入X作为贡献程度来对相关分数进行划分

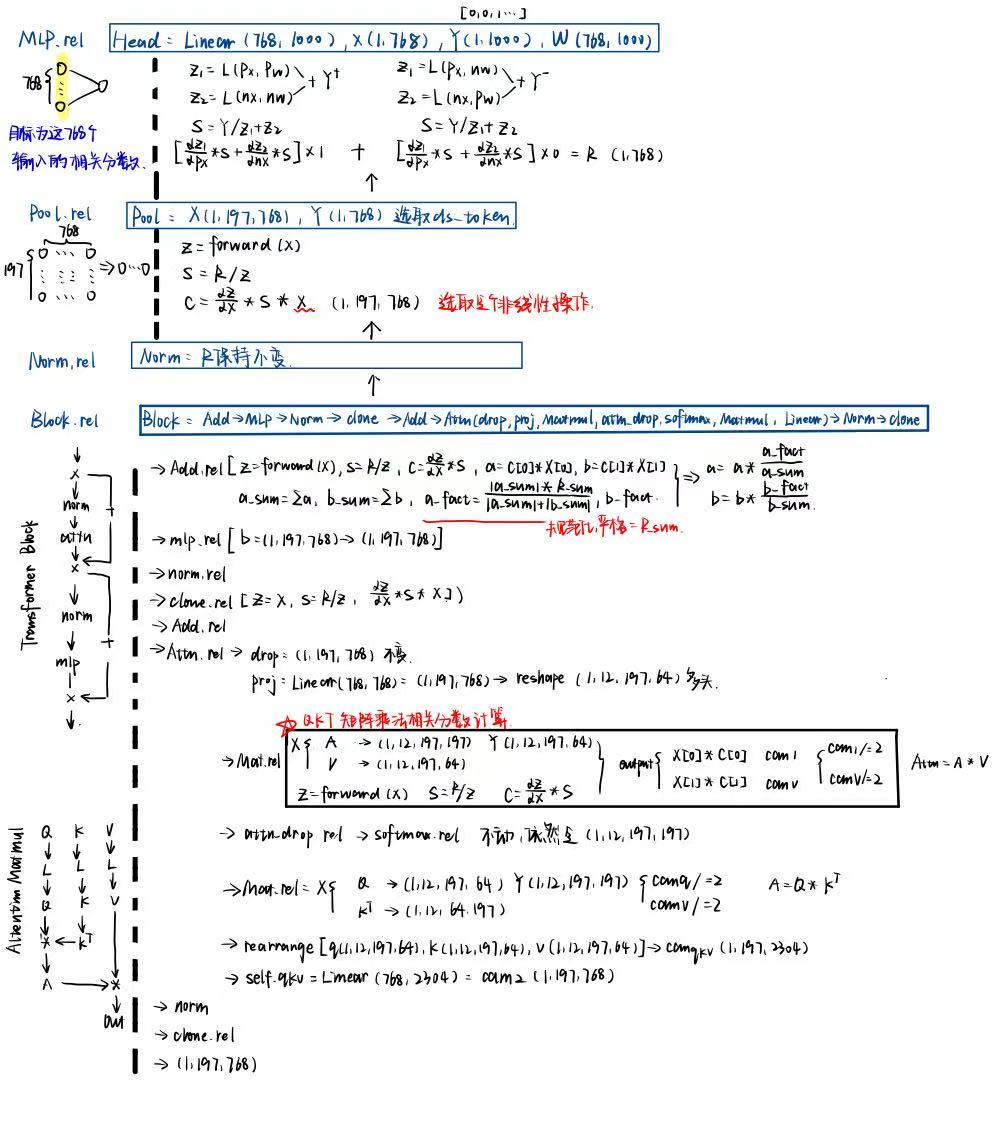
下面是官方的实现代码，full路线就是论文提出的这种梯度+相关分数的方法，里面提到的attention梯度*相关分数的部分就是在图中标红星的部位，矩阵相乘的相关分数计算模块，整体的注意力分数结果如下：

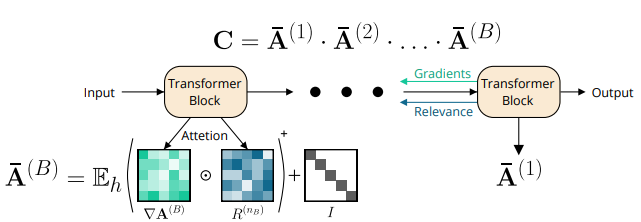
实验结果

对比的解释方法

Rollout：将所有层的注意力矩阵乘起来，得到一个整体的注意力“路径”

Raw attention：直接用第一层的注意力矩阵。

GradCAM：计算类别分数对最后一层特征图的梯度，然后加权求和

类似 LRP 或 partial LRP，但这些方法对不同类别输出结果差异不大，说明是“类无关”的。

图像扰动测试

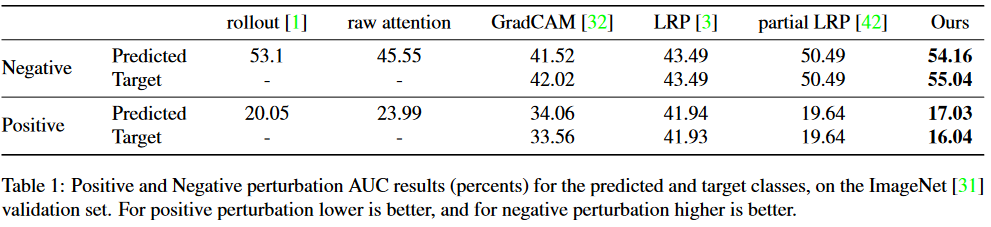
扰动测试（Perturbation Test）：用来测试解释图到底有没有指出“关键区域”。

  • Positive：先把重要区域遮住，看模型性能掉多少。

  • Negative：先遮住不重要的区域，看模型性能能否保持住。

  • 结果用 AUC（曲线下面积）表示。Positive 越小越好（掉得快），Negative 越大越好（保持好）。

分割测试

把解释图当作“图像分割图”，和真实标注对比。用 pixel accuracy, mIoU, mAP 来测。

文本任务（情感分析）

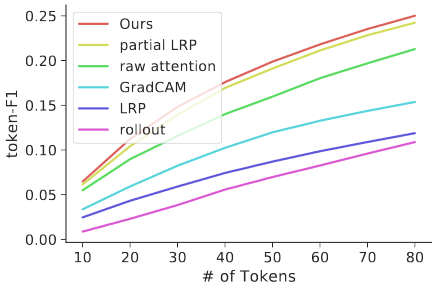
从一段评论中指出哪些词支持判断，用token-F1分数来评估，表示找出“重要词”的准确率和召回率的综合，OURs的方法效果最好，曲线在最上方。

消融实验

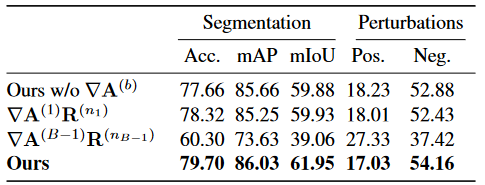
第一行去掉了attention梯度的反向传播 

第二行是只使用了第一层的attention梯度和对应的相关性分数

第三行是只使用了倒数第二层的attention梯度和对应的相关性分数。

网络标签：

相关问题