【洛谷】六个重要排序算法代码实现，时间复杂度和稳定性分析

文章目录

• 插入排序
• • 时间复杂度
  • 稳定性
• 选择排序
• • 时间复杂度
  • 稳定性
• 冒泡排序
• • 时间复杂度
  • 稳定性
• 堆排序
• • 时间复杂度
  • 稳定性
• 快速排序
• • 算法原理
  • 朴素快排缺陷
  • 优化一：随机选择基准元素
  • 优化二：数组分三块
  • 代码实现
  • 时间复杂度
  • 稳定性
• 归并排序
• • 时间复杂度
  • 稳定性

插入排序

插入排序的思想类似于我们玩扑克牌整理牌的过程，我们来看下面这个示例：

42之前的所有数都已经有序了，这时我们需要将42插入到前面有序数列的正确位置，首先42先和有序数列里最大的49比较，42比49小，将49往后移一位，42再和16比较，比16大，所以42就插入到16后面。

using namespace std;#include #include const int M = 1e5 + 10;vector<int> v(M);void insert_sort(int N){//第一个数默认有序，从第二个数开始插入，依次枚举待排序元素for (int i = 2; i <= N; i++){//v[i]的值有可能被覆盖int tmp = v[i];int j = i - 1;//比tmp大的v[j]统一右移while (j >= 1 && v[j] > tmp){v[j + 1] = v[j];j--;}v[j + 1] = tmp; //出循环要j--，所以插到j+1的位置}}int main(){int N;cin >> N;for (int i = 1; i <= N; i++){cin >> v[i];}insert_sort(N);for (int i = 1; i <= N; i++){cout << v[i] << \" \";}cout << endl;return 0;}

时间复杂度

如果数组有序，只会扫描⼀遍，时间复杂度为 O(n) 。
如果逆序，所有元素都会向后挪⼀次到合适位置，时间复杂度为 O(n2 ) 。
取最坏情况，两层嵌套循环，时间复杂度为O(n^2 )。

稳定性

插入排序是稳定的。
对于相等的元素，新元素会被插入到已排序区间中相等元素的后方，从而保留了原有的相对顺序。
举例说明：
假设有数组[2, 1, 2]（注意两个 2 的初始位置）：
已排序区间初始为 [2]，未排序区间为 [1, 2]；
插入 1 后，已排序区间变为[1, 2]；
插入最后一个 2 时，由于 2 等于已排序区间的最后一个元素 2，新元素会被插入到它的后面，最终结果为 [1, 2, 2]。

选择排序

每次找出未排序序列中最⼩的元素，然后放进有序序列的后⾯。比如一开始把整个序列遍历一遍找到最小的放在序列的开头，下一步就从剩下的序列里找最小的插到序列的第二个位置，直到序列全部有序。

//从无序数组里选择最小的插入到有序数组后面for (int i = 1; i <= N; i++) //待排序区间的首位置{for (int j = i; j <= N; j++) //找待排序数组里最小的元素{int pos = i; //假设最小元素下标为iif (v[j] < v[i]){pos = j; //将最小元素下标更新为j}swap(v[pos], v[i]);}}

时间复杂度

⽆论数组有序还是⽆序，在未排序区间内找最⼩值的时候，都需要遍历⼀遍待排序的区间，因此时间复杂度为 O(n^2 ) 。

稳定性

选择排序是不稳定的，核心原因在于它的交换逻辑可能破坏相等元素的相对位置，这种交换可能导致原本在前面的相等元素被换到后面，例如下面例子的2。插入排序是没有交换逻辑的，所以插入排序是稳定的。
举例说明：
例如数组 [2, 3, 2, 1]（两个 2 的初始位置是索引 0 和 2）：
第一步找到最小值 1（索引 3），与索引 0 的 2 交换，数组变为 [1, 3, 2, 2（原索引0）]。
待排序区间缩小为索引 1 到 3，找到最小值 2（索引 2），与索引 1 的 3 交换，数组变为 [1, 2（原索引2）, 3, 2（原索引0）]。
此时，原数组中 “索引 0 的 2 在索引 2 的 2 前面”，但排序后变成 “原索引 2 的 2 在原索引 0 的 2 前面”，相对位置被破坏，明显不稳定。

冒泡排序

冒泡排序(Bubble Sort)也是⼀种简单的排序算法。它的⼯作原理是每次检查相邻两个元素，如果前⾯的元素与后⾯的元素满⾜给定的排序条件，就将相邻两个元素交换。当没有相邻的元素需要交换时，排序就完成了。
由于在算法的执⾏过程中，较⼤的元素像是⽓泡般慢慢浮到数列的末端，故叫做冒泡排序。

void bubble_sort(int N){int flag = 1; //默认有序 //趟数(N-1趟)for (int i = N; i > 1; i--){ //待排序区间(1,i)for (int j = 1; j < i; j++){//v[j]更大就交换(把大的往后放)if (v[j] > v[j + 1]){swap(v[j], v[j + 1]);flag = 0;}}if (flag == 1)return;}}

时间复杂度

如果数组有序，只会扫描⼀遍，时间复杂度为 O(n) 。
如果逆序，所有元素都会向后冒⼀次到合适位置，时间复杂度为 O(n^2 ) 。

稳定性

标准（默认）实现的冒泡排序是稳定的排序算法，其稳定性源于 “仅交换值更大的相邻元素，不交换相等元素” 的逻辑。

堆排序

堆排序(Heap Sort)是指利⽤堆这种数据结构所设计的⼀种排序算法。本质上是优化了选择排序算法，如果将数据放在堆中，能够快速找到待排序元素中的最⼩值或最⼤值。
堆排序的过程分两步：

1. 建堆。升序建⼤堆，降序建⼩堆。 建堆过程，从倒数第⼀个⾮叶⼦节点开始，倒着⼀直到根结点位置，每个结点进⾏向下调整。
2. 排序。删除堆顶的逻辑。 每次将堆顶元素与堆中最后⼀个元素交换，然后将堆顶元素往下调整。直到堆中剩余⼀个元素，所有元素就都有序了。

因此，这里的堆排序仅需⽤到向下调整算法。
注意向下调整算法取vector的size时不能直接调v.size()，因为vector是n个val初始化的，所以它的size等于capacity，而vector本身的有效数据个数有可能没有填满整个vector。所以size应该为N + 1,因为这里vector是从下标为1的位置开始填充数据的。所以这里孩子和父亲结点的求法也和我们在数据结构初阶哪里讲的不一样，这里的求法如下：
父结点 = 孩子结点 / 2
左孩子结点 = 父结点 * 2
右孩子结点 = 父结点 * 2 + 1
注意建堆和排序的循环条件也要对应从之前的0变成1。

using namespace std;#include #include const int M = 1e5 + 10;int N;vector<int> v(M);void AdjustDown(int parent, int size){int child = 2 * parent;while (child < size){if (child + 1 < size && v[child + 1] > v[child]) //找左右孩子中较大的++child;if (v[child] > v[parent])swap(v[parent], v[child]);elsebreak;parent = child;child = 2 * parent;}}void heap_sort(){// 建堆for (int parent = (N + 1 - 1) / 2; parent >= 1; parent--){AdjustDown(parent, N + 1);}// 排序for (int tail = N; tail > 1; tail--){swap(v[1], v[tail]);//交换后再AdjustDown时应该--size了//本来第二个参数应该传tail+1的。现在应该传tailAdjustDown(1, tail); }}int main(){cin >> N;for (int i = 1; i <= N; i++){cin >> v[i];}heap_sort();for (int i = 1; i <= N; i++){cout << v[i] << \" \";}cout << endl;return 0;}

时间复杂度

堆排序的时间复杂度详细推理见：点这里
结论是： nlogn

稳定性

堆排序的不稳定性是由其 “基于堆结构的父子节点比较交换”逻辑决定的：调整堆时仅关注数值大小，不保留元素的原始位置信息，在排序过程中堆顶和末尾元素交换就可能破环相同元素的初始顺序，如(2,1,2)。

快速排序

算法原理

常规快排：在待排序区间中任取⼀个元素作为枢轴(pivot，或称基准值，通常选取区间⾸元素)，然后按照基准值⼤⼩将区间中元素分割成左右两部分，左侧区间中元素⼩于基准值，右侧区间中元素⼤于等于基准值，即基准值已经放在其该放的位置上，(即最后排完序基准值也在这个位置)该过程称为⼀次划分。划分结束后，再递归排基准值左侧，递归排基准值右侧，直到待排序区间长度为1时停止。
下面的例子是以待排序区间第一个值作为基准值实现的。

朴素快排缺陷

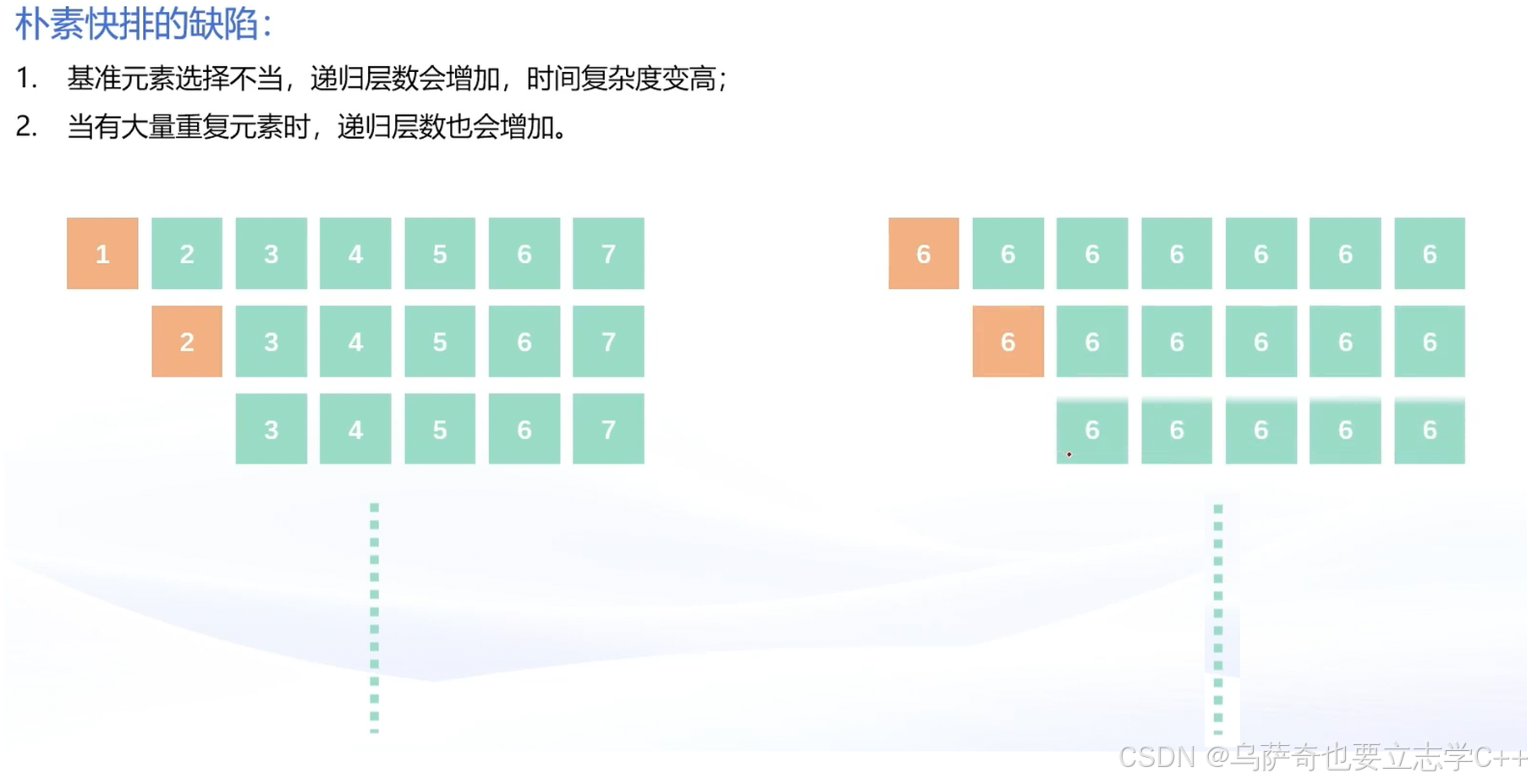
优化一：随机选择基准元素

先解决第一个问题：基准元素选择不当，递归层数会增加，时间复杂度变高。 解决方案：在待排序区间中，随机选择一个基准元素。利用 C++
提供的随机函数，在一个区间内随机选择一个元素作为基准。
随机函数：
srand(time(0))：种下一个随机数种子；
rand()：获得一个随机数；
rand() % (right - left + 1) + left：在 [left, right]区间内，随机选择一个数。

优化二：数组分三块

解决第二个问题：当有大量重复元素时，递归层数也会增加。
回忆一下之前在顺序表做过的一道题：《颜色分类》。这道题的核心就是数组分成三块：左边全是 0；中间全是 1；右边全是 2。
如果在此基础上稍作修改，变成：左边全部小于基准元素；中间全部等于基准元素；右边全部大于基准元素。那么，接下来仅需递归处理左右区间，中间区间就可以无需考虑。

代码实现

注意下面递归结束条件是if (left >= right)，而不是if (right - left <= 1)，因为left和right是闭区间，当left == right时区间长度为1，right - left == 1表示区间长度为2，需要继续往下递归。

using namespace std;#include #include const int M = 1e5 + 10;int N;vector<int> v(M);int get_random(int left, int right){return v[rand() % (right - left + 1) + left];}void quick_sort(int left, int right){//递归结束条件if (left >= right)return;//获取区间随机元素int key = get_random(left, right);//数组分三块int l = left - 1, r = right + 1, i = left;while (i < r){if (v[i] < key)swap(v[++l], v[i++]);else if (v[i] == key)i++;elseswap(v[--r], v[i]);}quick_sort(left, l);quick_sort(r, right);}int main(){srand(time(0));cin >> N;for (int i = 1; i <= N; i++){cin >> v[i];}quick_sort(1, N);for (int i = 1; i <= N; i++){cout << v[i] << \" \";}cout << endl;return 0;}

时间复杂度

如果每次基准元素都选择得当，数组划分的比较均匀，时间复杂度 = 递归层数 * N = N * logN。
如果划分不当，数组分布比较极端，时间复杂度退化成 N²。

分区操作：通过 while (i < r) 遍历当前区间 [left, right] 中的所有元素，完成一次分区（时间成本与区间长度成正比）。
递归调用：将问题拆分为两个子问题（左右子区间），分别递归处理。

解释： 如果每次分区都能将数组「几乎均匀」地分成两部分（例如 k ≈ n/2），此时递归树的结构是平衡的：(类似树形结构的递归)
第 1 层：处理长度为 n 的区间，成本 O(n)
第 2 层：处理两个长度为 n/2 的区间，总 cost O(n/2) + O(n/2) = O(n)
第 3 层：处理四个长度为 n/4 的区间，总 cost 4×O(n/4) = O(n)
…
第 log n 层：处理 n 个长度为 1 的区间，总 cost n×O(1) = O(n)
每一层的总 cost 都是 O(n)，而递归的层数是 logn（因为每次区间长度减半）。因此总时间复杂度为： 总 cost = 层数 × 每层 cost = O(log n) × O(n) = O(n log n)

如果每次分区都极度不均匀（例如每次选到的基准都是当前区间的最小值或最大值），此时递归树会退化为一条链：
第 1 层：处理长度为 n 的区间，成本 O(n)
第 2 层：处理长度为 n-1 的区间，成本 O(n-1)
第 3 层：处理长度为 n-2 的区间，成本 O(n-2)
…
第 n 层：处理长度为 1 的区间，成本 O(1)
总 cost 是 O(n) + O(n-1) + … + O(1) = O(n²)（等差数列求和）。

总结：平均 O (n log n)，最坏 O (n²)

稳定性

快速排序是不稳定的排序算法。
快速排序在分区过程中，会对元素进行交换（如代码中swap(v[++l],v[i++])或swap(v[–r], v[i])），可能导致相等元素的相对位置发生改变，就是在数组分块过程中当遇到小于基准值的数据时，交换时会把在最前面的等于基准值的数据换到最后面。

归并排序

归并排序(Merge Sort)是⽆论数据有什么特性，时间复杂度就能稳定 O(n log n) 的排序算法。
归并排序⽤的是分治思想。它的主要过程分两步：

1. 将整个区间从中间⼀分为⼆，先把左边和右边排序。
2. 然后将左右两个有序的区间合并在⼀起。 其中，如何让左右两边有序，就继续交给归并排序，因此归并排序是⽤递归来实现的，直到区间没有元素或者只有一个元素停止递归。

前面的快排有点类似树的前序遍历，因为快排会先选取随机元素并且数组分三块后再继续往下递归，而这里的归并排序有点类似后续遍历，它是一开始什么都不干先把数组⼀分为⼆然后继续递归，当递归返回时在合并两个有序的区间时排序。

小编在代码实现过程中有一些可以优化的地方，在这里给大家讲一下以供参考：
1、除以2我们通常写成右移一位，因为位运算比除法指令更高效。
2、当合并两个有序数组时需要开一个新数组空间，不要把创建数组写在递归函数里，最好在函数外创建一个全局临时数组以减少开销。
3、递归终止条件最好写成left >= right，不要去计算区间长度隐式判断，因为计算区间长度隐式判断依赖输入合法性，如果调用merge_sort(3, 2)就会出问题，因为left 和 right 是无符号类型，导致 right - left 计算结果为 极大的正数，此时len >= 2成立，会进入递归，最终导致数组访问越界。
4、因为归并排序是可以实现成稳定的，所以这里我们就实现成稳定的排序。想使其稳定需要将左区间的元素先放入临时数组tmp，由于左区间的元素在原数组中位置更靠前，排序后相等元素的相对顺序与原数组一致。
下面的代码示例第一个为初版，第二个为优化后的：

using namespace std;#include #include const int M = 1e5 + 10;int N;vector<int> v(M);void merge_sort(int left, int right){size_t len = right - left;size_t mid = left + len / 2; //mid为左区间最后一个元素下标if (len >= 2){merge_sort(left, mid); //递归左区间merge_sort(mid + 1, right); //递归右区间}//开新空间合并两个有序数组vector<int> v1(len + 1); //len为1表示有两个数据，所以开新空间需要len + 1//pv指向新数组头，pl、pl分别从头遍历两个原区间size_t pv = 0, pl = left, pr = mid + 1;//[left, mid] [mid + 1, right]while(pl <= mid && pr <= right){if (v[pl] > v[pr]){//小的往前放v1[pv++] = v[pr++];}else{v1[pv++] = v[pl++];}}if (pr > right){//把右区间剩余数据拷贝到新数组for (pl; pl <= mid; pl++){v1[pv++] = v[pl];}}else{//把左区间剩余数据拷贝到新数组for (pr; pr <= right; pr++){v1[pv++] = v[pr];}}//把新数组拷贝回原数组size_t j = 0; //新数组下标for (size_t i = left; i <= right; i++){v[i] = v1[j++];}}int main(){cin >> N;for (int i = 1; i <= N; i++){cin >> v[i];}merge_sort(1, N);for (int i = 1; i <= N; i++){cout << v[i] << \" \";}cout << endl;return 0;}using namespace std;#include #include const int M = 1e5 + 10;int N;vector<int> v(M);vector<int> tmp(M);void merge_sort(size_t left, size_t right){if (left >= right)return;size_t mid = (left + right) >> 1; //mid当作左区间最后一个元素下标merge_sort(left, mid); //递归左区间merge_sort(mid + 1, right); //递归右区间//pv指向新数组，cur1、cur2分别从头遍历两个原区间size_t pv = left, cur1 = left, cur2 = mid + 1;//[left, mid] [mid + 1, right]while (cur1 <= mid && cur2 <= right){if (v[cur1] > v[cur2]){//小的往前放tmp[pv++] = v[cur2++];}else{tmp[pv++] = v[cur1++];}}while(cur1 <= mid)tmp[pv++] = v[cur1++];while(cur2 <= right)tmp[pv++] = v[cur2++];//把新数组拷贝回原数组for (size_t i = left; i <= right; i++){v[i] = tmp[i];}}int main(){cin >> N;for (int i = 1; i <= N; i++){cin >> v[i];}merge_sort(1, N);for (int i = 1; i <= N; i++){cout << v[i] << \" \";}cout << endl;return 0;}

时间复杂度

前面已经介绍过了，归并排序时间复杂度始终为nlogn。

稳定性

稳定性前面也介绍过了，归并排序是稳定的。

以上就是小编分享的全部内容了，如果觉得不错还请留下免费的关注和收藏
如果有建议欢迎通过评论区或私信留言，感谢您的大力支持。
一键三连好运连连哦~~