迭代器和生成器&数据结构和算法（基础）

day6 昨天自习没上课，所以今天是第六天，今天这四个内容也是非常的概念，难记得很，晚自习来捋一下思路

迭代器和生成器

迭代器

迭代器（Iterator）是 Python 中的一种对象，用于在数据集合中逐个访问元素，而不需要暴露数据集合的底层实现。它提供了一种遍历集合元素的标准方式，适用于任何支持迭代的数据结构，如列表、元组等，range()就是一个迭代器

迭代器是一个实现了__iter()__和__next__()方法的对象，使得可以逐步遍历它的元素。

特点：

手动管理：需要显式地实现 __iter__() 和 __next__() 方法

状态管理：迭代器需要自己管理迭代的状态，包括当前位置和结束条件

内存使用：内存使用取决于迭代器的实现，通常是惰性计算（即按需生成数据）

迭代器底层实现：

# 定义一个自定义的迭代器类class myl: # 初始化方法，接收起始值和结束值 def __init__(self,start,end): self.start = start # 设置起始值 self.end = end # 设置结束值 # 实现__iter__方法，返回迭代器对象本身 def __iter__(self): return self # 实现__next__方法，定义如何获取下一个元素 def __next__(self): # 如果起始值大于结束值，说明迭代完成，抛出StopIteration异常 if self.start > self.end: raise StopIteration # 保存当前值 value = self.start # 起始值自增1，为下一次迭代做准备 self.start += 1 # 返回当前值 return value# 创建myl类的实例，设置范围从1到10i = myl(1,10)# 使用for循环遍历迭代器，打印每个值for j in i: print(j)

生成器

根据程序员制定的规则循环生成数据，当条件不成立时则生成数据结束。数据不是一次性全部生成出来，而是使用一个，再生成一个，可以节约大量的内存

生成器推导式：

generator = (expression for item in iterable if condition) 

yield生成器

将yield后面的值返回

# 定义一个生成器函数，接收一个参数ndef myg(n): # 使用for循环从0到n-1迭代 for i in range(n): print(\"开始生成下一个值\") # 在每次迭代开始时打印提示信息 yield i # 使用yield关键字返回当前值i，暂停函数执行并返回给调用者 print(f\"值 {i} 已返回，准备生成下一个值\") # 在每次迭代结束时打印提示信息print(\"创建生成器对象，但不立即执行函数体\")# 调用生成器函数myg(5)，创建一个生成器对象，但不立即执行函数体generator = myg(5)print(\"开始迭代生成器:\")# 使用for循环遍历生成器，每次从生成器获取一个值并打印for i in generator: print(f\"接收到值: {i}\") print(\"--- 暂停执行，等待下一次迭代 ---\")

生成器和迭代器的区别

实现方式

迭代器：需要实现 __iter__() 和 __next__() 方法，手动管理迭代状态

生成器：通过 yield 关键字简化实现，自动管理迭代状态

代码复杂度

迭代器：通常需要更多的代码来管理状态和迭代逻辑

生成器：代码更简洁，更容易理解和维护

性能与内存

迭代器：性能和内存使用取决于实现，通常也是惰性计算。

生成器：由于使用了 yield，内存使用和性能优化自动管理，适合处理大数据或流数。

使用场景

迭代器：适合需要对迭代过程进行高度控制，或者需要自定义复杂的迭代逻辑时使用

生成器：适合需要简洁地生成序列数据，尤其是在处理大数据或需要按需生成数据时，能够节省内存和提高性能

生成器的应用场景

这里没有txt是运行不了的，就是个例子

# 导入数学模块，用于向上取整计算import mathdef dataset_loader(b_s): \'\'\' 以批处理方式加载数据集的生成器函数 :param b_s: 批处理大小(batch size)，即每批包含的数据行数 :return: 每批数据的生成器 \'\'\' # 打开并读取周杰伦歌词文件，使用utf-8编码以正确处理中文字符 with open(r\"C:\\Users\\33094\\Documents\\Tencent Files\\jaychou_lyrics.txt\", encoding=\'utf-8\') as f: lines = f.readlines() # 计算文件总行数 line_count = len(lines) # 使用向上取整计算需要多少个批次才能处理完所有数据 # 例如：100行数据，每批处理10行，则需要10个批次 # 如果100行数据，每批处理30行，则需要4个批次(ceil(100/30)=4) b_c = math.ceil(line_count/b_s) # 循环处理每个批次 for i in range(b_c): # 计算当前批次的起始行索引 start_index = i * b_s # 计算当前批次的结束行索引 end_index = (i+1) * b_s # 从原始数据中切片提取当前批次的数据 # 注意：即使end_index超出了列表长度，Python也会正确处理 b_d = lines[start_index:end_index] # 使用yield关键字返回当前批次的数据，使函数成为一个生成器 # 这样可以节省内存，不必一次性加载所有数据到内存中 # 同时返回批次编号，便于标识当前是第几批数据 yield (i+1, b_d)# 当脚本被直接运行时执行以下代码（而不是被导入时）if __name__ == \'__main__\': # 创建一个批处理大小为10的生成器实例 # 每批将包含10行歌词数据 my_g = dataset_loader(10) # 遍历生成器，依次获取每批数据和批次编号 for batch_number, batch_data in my_g: # 输出当前是第几批数据的标识 print(f\"===== 这是第{batch_number}批数据 =====\") # 逐行输出当前批次的数据 for line in batch_data: print(line.strip()) # strip()去除行末的换行符 # 在每批数据后添加两个空行，形成清晰的批次间隔 print(\"\\n\")

数据结构与算法

数据结构是存储、组织数据的方式 ,指相互之间存在一种或多种特定关系的数据元素的集合

数据的种类有很多：字符串、整数、浮点数、布尔值、列表、元组、集合、字典

为了满足业务需求实现业务目的的各种方法和思路就是算法

同样的数据,同样的目的, 不同的算法,不同的方法和思路,效率就会不同

通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率 , 数据结构往往影响着算法的效率

数据结构只是静态的描述了数据元素之间的关系，是存储和组织数据的方式。

高效的程序需要在数据结构的基础上设计和选择算法

算法是为了解决实际问题而设计的，数据结构是算法需要处理问题的载体

算法

算法的特性

算法是独立存在的一种解决问题的方法和思想

对于算法而言，实现的语言并不重要，重要的是思想

五大特性：有输入；有输出；有穷性；确定性（无二义性）；可行性

算法的时间效率衡量

实现算法程序的执行时间可以反应出算法的效率，即算法的优劣

假定计算机执行算法每一个基本操作的时间是固定的一个时间单位 , 那么有多少个

基本操作就代表会花费多少时间单位 , 由此可以忽略机器环境的影响而客观的反应算法

的时间效率

代码执行总时间(T) = 操作步骤数量 * 操作步骤执行时间

T = (大整体 * 子整体 * 基本操作) * 操作步骤执行时间

假定计算机执行算法每一个基本操作的时间是固定的一个时间单位

T = 操作步骤总数(基本操作 * 子整体 * 大整体)

时间复杂度

时间复杂度是算法运行时间T随输入规模n增长的变化趋势度量，常用大O符号表示，通常用来衡量一个算法的优劣，通俗点来说时间复杂度可以衡量一个“算法的量级”

大O记法

算法一 : T(n) = n3 * 10

算法一优化 : T(n) = n3 * 10   => T(n) = O(n^3)

计算规则：

①基本操作

         时间复杂度为O(1)

②顺序结构

        时间复杂度按加法进行计算

③循环结构

        时间复杂度按乘法进行计算,注意次要项和常数项可以忽略

④分支结构

        时间复杂度取最大值

⑤判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略

⑥在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

例：

基本操作：

sum = 100 +200^2

O(1)

顺序结构：

x = 100

y = 200

c = a + b

O(1)

循环结构：

for i in range(0,5)

    for x in range(0,n):

        print(x)

O(n)

等

最优最坏的时间复杂度

最优时间复杂度: 反映的只是最乐观最理想的情况，没有参考价值。

最坏时间复杂度: 算法的一种保证，表明算法在此种程度的基本操作中一定能完成工作

平均时间复杂度：是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度

常见的时间复杂度

O(logn)：大O计数法：时间T与问题的规模变化曲线；二分法

O(nlogn)：一个for循环是n 另外一个for循环是二分法，组合在一起

所消耗的时间从小到大:

O(1) < O(logn) < O(n)  < O(n2) < O(n3)

时间复杂度越低，效率越高

空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的度量

类似于时间复杂度，一个算法的空间复杂度S(n)定义为该算法所耗费的存储空间，也使用大O记法。

和时间复杂度类似，空间复杂度一般常见的有：

O(1) < O(logn) < O(n)  < O(n2) < O(n3)

相同的概念不再赘述

数据结构

内存的存储结构

内存是以字节为基本存储单位的, 每个基本存储空间都有自己的地址 ,

整形(int) :  4个字节

字符(char):  1个字节

数据结构的分类

线性结构

线性结构就是数据结构中各个结点具有线性关系

线性结构的特点:

①  线性结构是非空集

②  线性结构所有结点都最多只有一个直接前驱结点和一个直接后继结点

典型的线性结构 : 栈、队列等

非线性结构

非线性结构就是数据结构中各个结点之间具有多个对应关系

非线性结构的特点:

① 非线性结构是非空集

② 非线性结构的一个结点可能有多个直接前驱结点和多个直接后继结点

典型的非线性结构 : 树结构和图结构等

线性结构顺序表存储方式

分类：

①顺序表 : 将元素顺序地存放在一块连续的存储区里，元素间的顺序关系由它们的存储顺序自然表示

②链表 : 将元素存放在通过链接构造起来的一系列存储块中 , 存储区是非连续的

顺序表元素顺序地存放在一块连续的存储区里，具体的存储方式的两种情况:

一体式结构

num会记录列表的首元素地址0x11

由于列表所有的数据都是整形,大小都为4个字节,偏移量为4

第一个元素10 : 通过0x11偏移4*0个字节可以找到

第二个元素20 : 通过0x11偏移4*1个字节可以找到

第三个元素30 : 通过0x11偏移4*2个字节可以找到

查找数据的公示 : 0x11 偏移 4 * (n-1) 个字节

分离式结构

num = [ 10 , “A”, “ABC”]

地址的大小为4字节是固定的 , 我们可以不存储数据 , 而是存储地址

无论一体式结构还是分离式结构，顺序表在获取数据的时候直接通过下标偏移就可以找到数据所在空间的地址 , 而无需遍历后才可以获取地址 . 所以顺序表在获取地址操作时的时间复杂度 : O(1)

顺序表的结构和扩充

存储结构：数据区和信息区

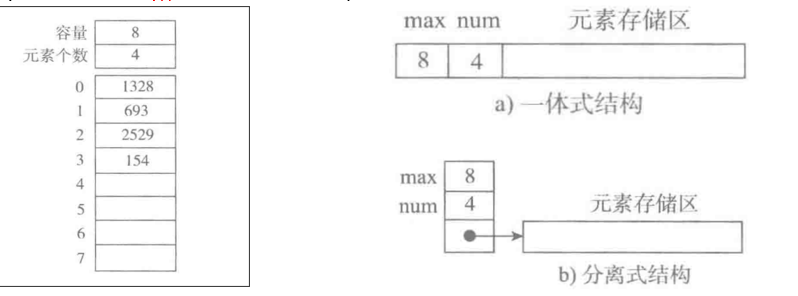
扩充

两种策略：

①每次扩充增加固定数目的存储位置，如每次扩充增加10个元素位置，这种策略可称为线性增长

特点：节省空间，但是扩充操作频繁，操作次数多。

②每次扩充容量加倍，如每次扩充增加一倍存储空间。

特点：减少了扩充操作的执行次数，但可能会浪费空间资源 , 以空间换时间，推荐的方式

顺序表增加与删除元素

增加元素：

a. 尾端加入元素，时间复杂度为O(1)

b. 非保序的加入元素（不常见），时间复杂度为O(1)   比如：在指定位置1号位置加入111元素

c. 保序的元素加入，时间复杂度为O(n)

删除元素：

a. 删除表尾元素，时间复杂度为O(1)

b. 非保序的元素删除（不常见），时间复杂度为O(1)，比如：在指定位置删除（1号位置）删除111

c. 保序的元素删除，时间复杂度为O(n)

链表的结构

链表 : 将元素存放在通过链接构造起来的一系列存储块中 , 存储区是非连续的

顺序表存储时需要连续的内存空间，当要扩充顺序表时会出现以下情况：

内存不充足时，不易找到连续的内存空间；完成不了扩展扩充

链表则不需要连续的存储空间

单链表(单向链表)是链表的一种形式，每个结点包含两个域：元素域和链接域 

这个链接指向链表中的下一个结点 , 而最后一个结点的链接域则指向一个空值None

①表元素域item用来存放具体的数据

②链接域next用来存放下一个结点的位置

③变量head指向链表的头结点（首结点）的位置，从head出发能找到表中的任意结点

顺序表和链表的比较：

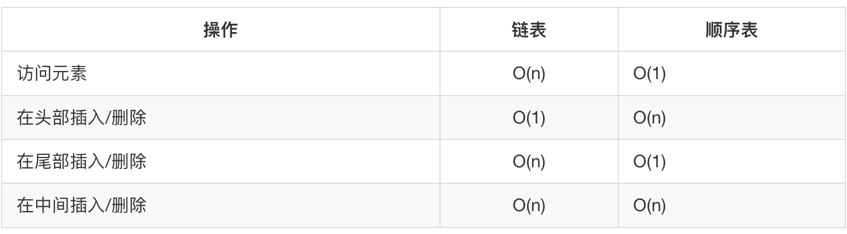
链表代码的实现

# 创建一个单链表的的节点对象，充当节点类，有数据域和指针域。class SingleNode(object): # 初始化节点属性 def __init__(self, item): # 数据域 self.item = item # 指针域 self.next = None

# 创建链表类from SingleNode import SingleNodeclass SingleLinkList(object): # 初始化属性，用head属性指向链表的第一个节点 def __init__(self, node): # 头节点是链表的第一个节点 self.head = node # 判断链表是否为空 def is_empty(self): \"\"\" 判断链表是否为空 如果head属性是None，链表为空 如果head属性不是None，链表不为空 :return: True 链表为空，False 链表不为空 \"\"\" return self.head == None # 获取链表的长度 def length(self): \"\"\" 获取链表的长度 遍历链表所有节点，统计节点个数 :return: 节点数量即链表长度 \"\"\" # 定义变量count表示节点数量 count = 0 # 定义变量cur表示当前节点，从头节点开始 cur = self.head # 当当前节点不为空时循环处理 while cur is not None: count += 1 # 节点数量加1 cur = cur.next # 获取下一个节点 return count # 遍历链表 def travel(self): \"\"\" 遍历链表并打印每个节点的数据域 :return: \"\"\" cur = self.head while cur is not None: print(cur.item) # 打印当前节点数据 cur = cur.next # 移动到下一个节点 # 在链表头部添加元素 def add(self, item): # 将传入的item封装成节点 new_node = SingleNode(item) # 新节点指向原来的头节点 new_node.next = self.head # 设置新节点为新的头节点 self.head = new_node # 在链表尾部添加元素 def append(self, item): # 将传入的item封装成节点 new_node = SingleNode(item) # 判断链表是否为空 if self.is_empty(): self.head = new_node # 空链表直接设为头节点 else: # 遍历找到最后一个节点 cur = self.head while cur.next is not None: cur = cur.next cur.next = new_node # 在末尾添加新节点 # 在链表指定位置添加元素 def insert(self, pos, item): # 场景1：pos<=0，在头部添加 if pos = self.length(): self.append(item) # 场景3：pos在中间位置 else: count = 0 cur = self.head # 找到插入位置前一个节点 while count < pos - 1: count += 1 cur = cur.next # 创建新节点 new_node = SingleNode(item) new_node.next = cur.next cur.next = new_node # 插入新节点 # 删除指定位置的元素（未实现） def remove(self, item): \"\"\" 删除链表中第一个值等于item的节点 :param item: 要删除的节点的值 :return: None \"\"\" # 定义变量pre表示当前节点的前一个节点 pre = None # 定义变量cur表示当前节点，从头节点开始 cur = self.head # 遍历链表寻找要删除的节点 while cur is not None: # 找到要删除的节点 if cur.item == item: if cur == self.head:  self.head = cur.next  cur = None else:  pre.next = cur.next  cur = None break else: pre = cur cur = cur.next # 查找指定元素的位置（未实现） def search(self, item): \"\"\" 查找指定元素是否在链表中 :param item: 要查找的元素值 :return: True 元素存在于链表中，False 元素不存在于链表中 \"\"\" # 定义变量cur表示当前节点，从头节点开始 cur = self.head # 遍历链表寻找要查找的节点 while cur is not None: # 找到要查找的节点 if cur.item == item: return True # 移动到下一个节点 cur = cur.next # 遍历完整个链表都没找到，返回False return False

from SingleLinkList import SingleLinkListfrom SingleNode import SingleNodeif __name__ == \'__main__\': # 创建三个节点对象 sn1 = SingleNode(10) # 创建第一个节点，数据为10 sn2 = SingleNode(20) # 创建第二个节点，数据为20 sn3 = SingleNode(30) # 创建第三个节点，数据为30 # 建立节点间的连接关系 sn1.next = sn2 # 第一个节点指向第二个节点 sn2.next = sn3 # 第二个节点指向第三个节点 # 创建链表对象，头节点为sn1 sl1 = SingleLinkList(sn1) # 测试链表的基本功能 # 判断链表是否为空 print(f\"链表是否为空：{sl1.is_empty()}\") # 应该输出False # 获取链表长度 print(f\"链表长度：{sl1.length()}\") # 应该输出3 # 遍历链表打印元素 print(\"链表元素：\") sl1.travel() # 应该输出10, 20, 30 print(\"--------------------\") # 在头部添加元素0 sl1.add(0) print(\"头部添加0后：\") sl1.travel() # 应该输出0, 10, 20, 30 print(\"--------------------\") # 在尾部添加元素40 sl1.append(40) print(\"尾部添加40后：\") sl1.travel() # 应该输出0, 10, 20, 30, 40 print(\"--------------------\") # 在位置2插入元素100（插入到索引为2的位置） sl1.insert(2, 100) print(\"位置2插入100后：\") sl1.travel() # 应该输出0, 10, 100, 20, 30, 40 # 测试空链表功能 # sl2 = SingleLinkList(None) # print(f\"链表是否为空：{sl2.is_empty()}\") # 应该输出True

总结：

概念开会，真的很枯燥，重点在生成器和时间复杂度那块，其他的了解理解即可