【每天一个知识点】生成对抗聚类（Generative Adversarial Clustering, GAC）

📘 生成对抗聚类（Generative Adversarial Clustering, GAC）

一、研究背景与动机

聚类是无监督学习中的核心任务。传统方法如 K-means、GMM、DBSCAN 等难以适应高维、非线性、复杂结构数据。

生成对抗聚类（GAC） 融合了生成对抗网络（GAN）的生成能力和聚类目标，通过对抗训练提升聚类质量，适用于图像、语音、生物信息等复杂数据场景。

---

二、整体架构设计

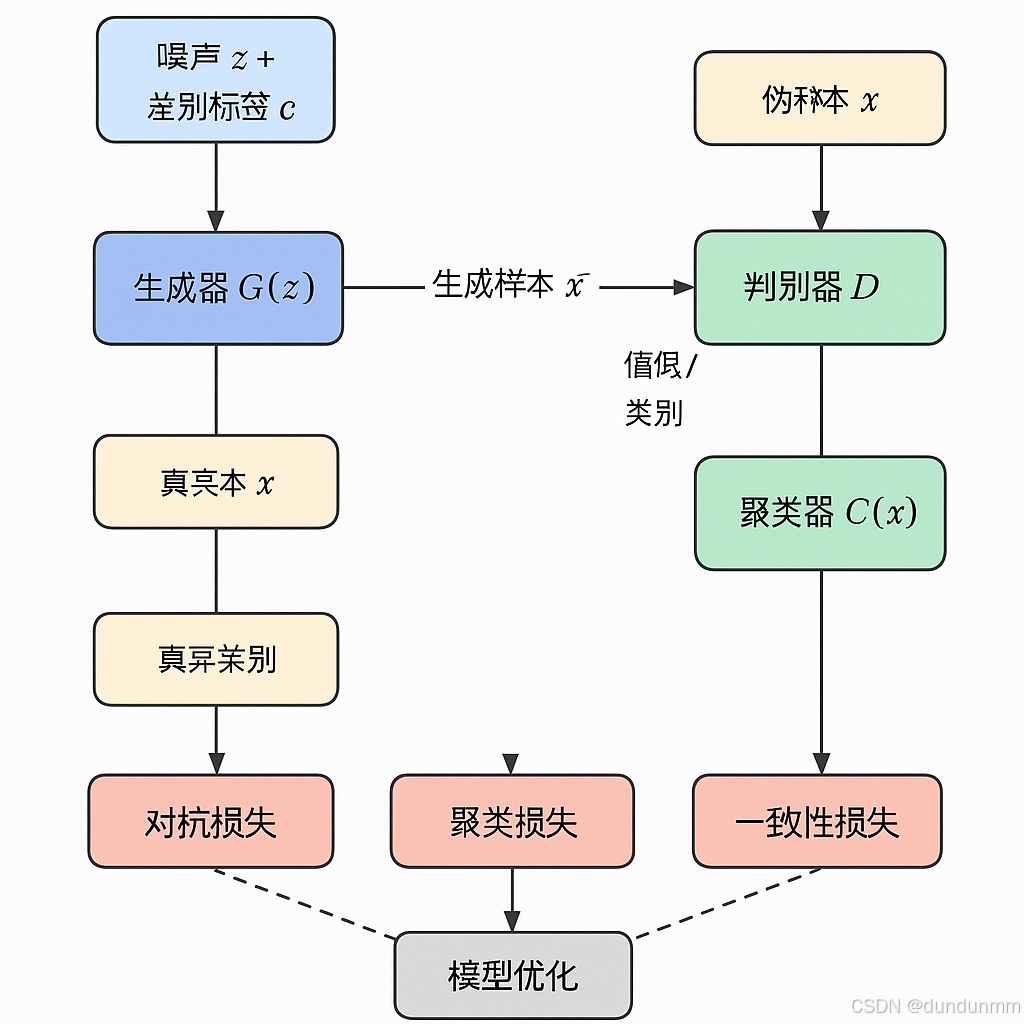
✳️ 模块结构

• 输入：

  • 噪声向量 z ~ p(z)
  • 真实样本 x ∈ ℝ^d

• 模块组成：

  1. 生成器 G(z)：生成伪样本 x̂ = G(z)
  2. 判别器 D(x)：判别真实样本与伪造样本
  3. 聚类器 C(x)：输出聚类标签或类别分布

• 输出：

  • 聚类标签或聚类概率

---

🧮 常用损失函数组合

1. 对抗损失（GAN Loss）

min ⁡ G max ⁡ DE x ∼ p d a t a [ log ⁡ D ( x ) ] + E z ∼ p z [ log ⁡ ( 1 − D ( G ( z ) ) ) ] \\min_G \\max_D \\mathbb{E}_{x \\sim p_{data}}[\\log D(x)] + \\mathbb{E}_{z \\sim p_z}[\\log(1 - D(G(z)))] Gmin​Dmax​Ex∼pdata​​[logD(x)]+Ez∼pz​​[log(1−D(G(z)))]

2. 聚类损失（Clustering Loss）

   • KL散度
   • 互信息最大化
   • 类别中心距离最小化

3. 一致性损失（Reconstruction Loss）

   • 潜变量恢复损失
   • 保证潜空间结构的一致性

---

三、典型算法代表

✅ 1. ClusterGAN

• 设计思路：

  • 将 one-hot 聚类标签作为生成器输入
  • 强制生成器学习具有明确聚类结构的样本
  • 判别器输出真假与聚类标签

• 损失组合：

L G A C= L G A N+ λ 1L r e c+ λ 2L c l u s t e r \\mathcal{L}_{GAC} = \\mathcal{L}_{GAN} + \\lambda_1 \\mathcal{L}_{rec} + \\lambda_2 \\mathcal{L}_{cluster} LGAC​=LGAN​+λ1​Lrec​+λ2​Lcluster​

---

✅ 2. InfoGAN

• 方法：

  • 引入潜变量 c
  • 最大化互信息 $I(c;G(z,c))$ 使生成结果与类别相关联

• 优势：

  • 可解释性强
  • 适用于图像/语音等任务

---

✅ 3. VaDE（变分自编码 + GMM）

• 方法：
  • 用 VAE 建模潜变量空间
  • 用 GMM 对潜变量进行聚类建模
  • 虽非 GAN，但在聚类效果上表现优异

---

四、训练流程图（Mermaid）

Z[噪声 z + 类别标签 c] --> G[生成器 G(z, c)]G --> Xhat[生成样本 x̂]X[真实样本 x] --> D[判别器 D]Xhat --> DD -->|真假+类别| 判别输出Xhat --> C[聚类器 C(x)]X --> Csubgraph 损失函数组合 D -.-> Ladv[对抗损失] C -.-> Lclu[聚类损失] G -.-> Lrec[一致性损失]endLadv & Lclu & Lrec --> Update[模型优化]

五、典型应用案例

应用领域 示例任务 说明 图像处理 MNIST, CIFAR 聚类 无监督图像分类 生物信息 scRNA-seq 聚类 基因表达数据建模 异常检测 工业/网络攻击检测 识别离群样本 语音识别 说话人聚类 基于音频片段分组识别

---

六、优势与挑战

✅ 优势

• 能生成具有聚类结构的数据分布
• 可实现端到端的聚类训练
• 潜变量空间具有可解释性
• 支持无监督类别发现

❌ 挑战

• 训练过程不稳定（GAN 原生缺陷）
• 聚类准确率对超参数敏感
• 潜空间结构评估较困难
• 初始标签或聚类数不易确定

---

七、可复现资源与工具包

名称 链接 内容说明 ClusterGAN https://github.com/mukulkhanna/ClusterGAN PyTorch 实现 InfoGAN https://github.com/openai/InfoGAN OpenAI 实现 scDEC https://github.com/kimmo1019/scDEC 单细胞RNA-seq聚类工具

---

八、总结与展望

生成对抗聚类将生成建模与结构发现相融合，在无监督学习领域展现出巨大潜力。

未来研究方向包括：

• 训练稳定性提升（如 Wasserstein GAN, Spectral Normalization）
• 聚类数自动推断机制
• 多模态 GAC 扩展（图像 + 文本等）
• 在生物医学、遥感等地方的定制化设计