23-NeurIPS-Self-Supervised Learning of Representations for Space Generates Multi-Modular Grid Cells

Author

Ila Rani Fiete, Sanmi Koyejo课题组

Rylan Schaeffer, Computer Science, Stanford University

Mikail Khona, Physics, MIT

Schaeffer R, Khona M, Ma T, et al. Self-supervised learning of representations for space generates multi-modular grid cells[J]. Advances in Neural Information Processing Systems, 2023, 36: 23140-23157.

Abstract

Why multi-periodic grid representation？

1) theoretical analysis: deduce the mathematical properties that the grid code possesses.

2) trains deep RNNs: identify the optimization problem that grid cells solve.

Mathematical analysis: an algebraic code with high capacity and intrinsic error-correction. But to date, there is no satisfactory synthesis of core principles that lead to multi-modular grid cells in deep RNN.

This work: 

1) Identify key insights from four families of approaches to answering the grid cell question: coding theory, dynamical systems, function optimization and supervised deep learning.

2) approach is a self-supervised learning (SSL) framework - including data, data augmentations, loss functions and a network architecture - motivated from a normative perspective, without access to supervised position information or engineering of particular readout representations as needed in previous approaches. The networks and emergent representations generalize well outside their training distribution.

3 Notation and Terminology

每一时刻，神经元群体的活动 g 都约束在N维超球的正象限。（？Equinorm coding states

4 Insights from Grid Cell Modeling Approaches

4.1 Insights from Coding Theory

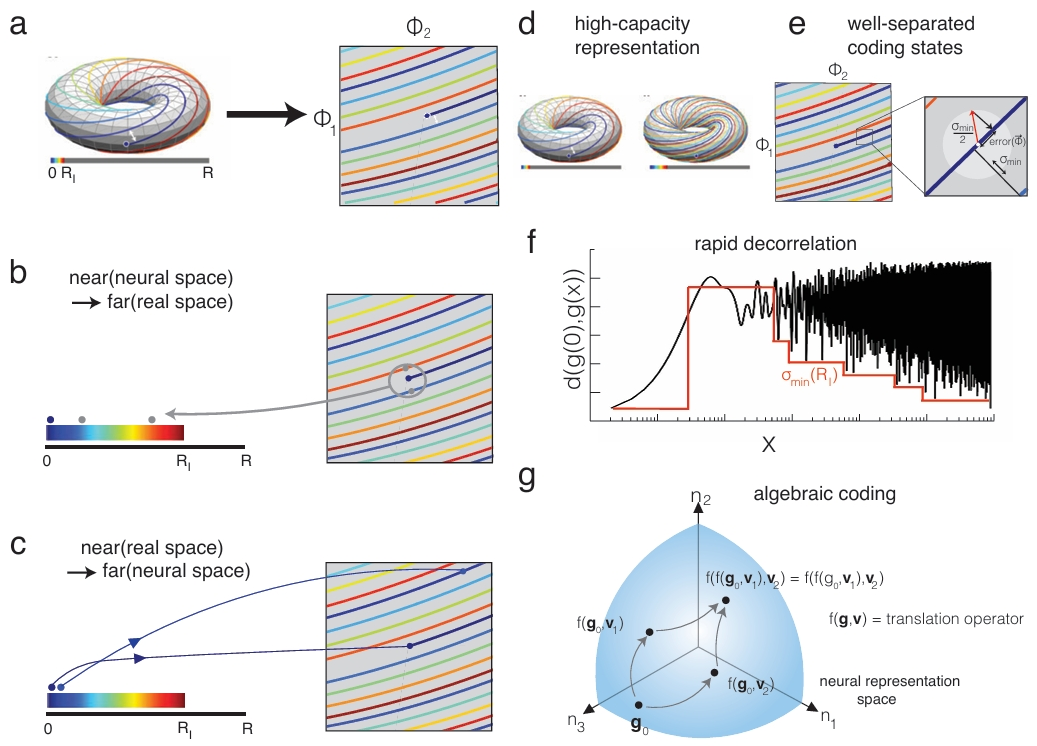
Figure 2: Mammalian grid cells and their coding theoretic properties. (a) 1D是torus，why 2D也是呢？orientation的分布-是因为上游的线性组合-用来error correct？

Exponential capacity; Separation; Decorrelation; Equinorm coding states;  Ease of update; Algebraic; Whitened representation（对于真实空间中的给定位移，所有网格模块的更新量是相似的）

4.2 Insights from Dynamical Systems

path invariant - continuous attractor

The lessons are thus twofold: the data and loss function(s) should together train the network to learn path invariant representations and continuous attractor dynamics, and the dynamical translation operation of the recurrent neural networks should architecturally depend on the velocity.

4.3 Insights from Spatial Basis Function Optimization

If one path-integrates with action-dependent weight matrices, then one must use a spatial neural code 𝒈​(𝒙) of a particular parametric form:

One can then define a loss function and optimize parameters to discover which loss(es) results in grid-like tuning, possibly under additional constraints.

4.4 Insights from Supervised Deep Recurrent Neural Networks

a common origin based on the eigendecomposition of the spatial supervised targets (putatively: place cells) which results in periodic vectors

Shortcomings: 1) the learned representations are set by the researcher, not by the task or fundamental constraints; 2) bypasses the central question of how agents learn how to track their own spatial position; 3) previous supervised path-integrating recurrent neural networks either do not learn multiple grid modules or have them inserted via implementation choices, oftentimes due to statistics in the supervised targets; 4) supervised networks fare poorly once the spatial trajectories extend outside the training arena box.

——remove supervised targets altogether, and instead directly optimize the relative placements of internal neural representations via self-supervised learning. In other words, we endorse the coding-theoretic perspective as the target for optimization, which is naturally fit for self-supervised learning.

5 Self-Supervised Learning of Representations for Space

an appropriate SSL framework (comprising training data, data augmentations, loss functions and architecture).

5.1 Data Distribution and Data Augmentations

Each batch: shared initial state 𝒈0, B permuted velocity trajectories (drawn i.i.d. from a uniform distribution)

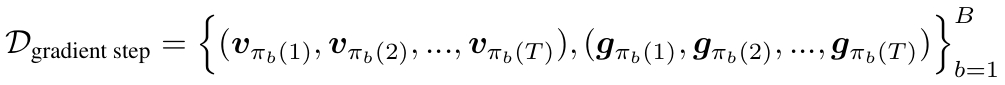
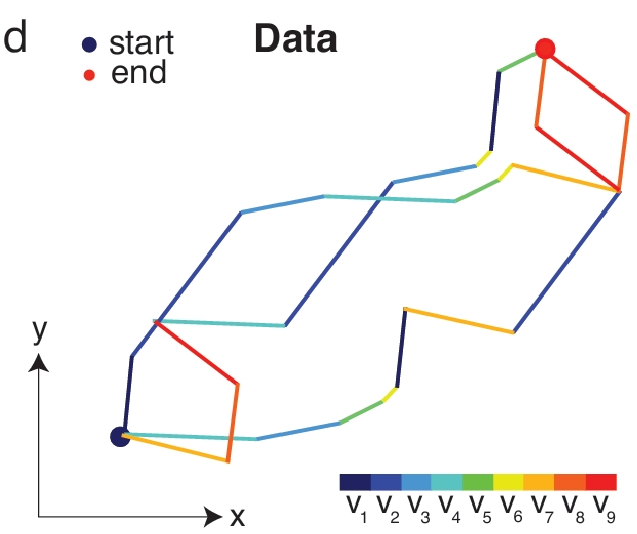
                Fig 3d

5.2 Recurrent Deep Neural Network Architecture

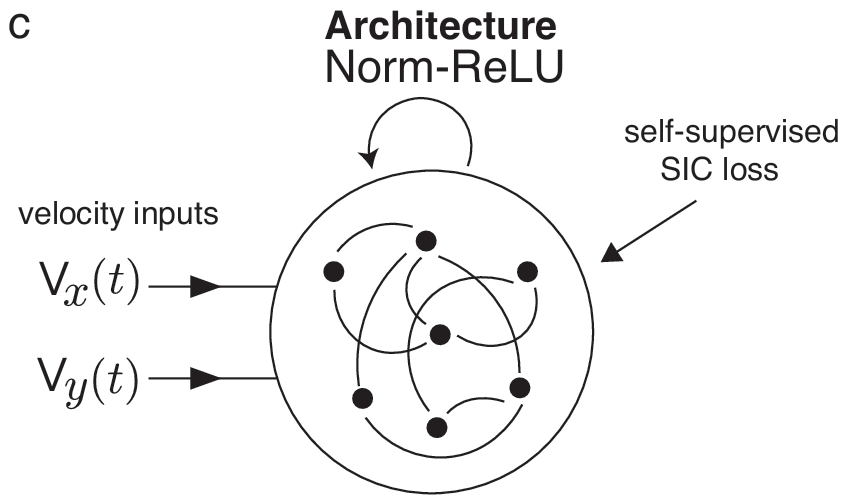
                                        Fig 3c

Representations at different points in space are related only by a function of velocity, thereby ensuring that the transformation applied to the state is the same so long as the velocity is the same.

5.3 Loss Functions

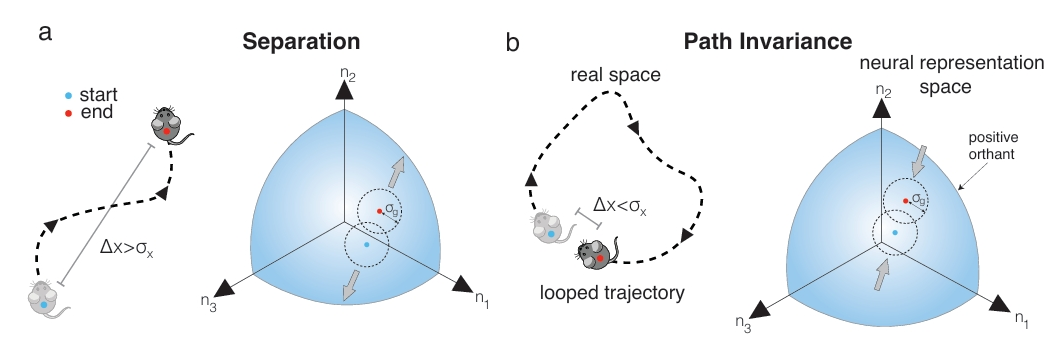
Fig 3a-b

SIC（Separation-Invariance-Capacity）损失函数组合​​：

• 分离损失（Separation Loss）​​：鼓励不同空间位置的神经表征保持距离。这有助于区分不同的地点。
• ​​路径不变性损失（Path Invariance Loss）​​：这是最核心的设计之一。它强制模型学习到的神经表征对达到同一空间位置的不同路径保持不变。这直接编码了路径积分的关键特性，即无论如何移动，只要最终到达同一点，其内部表征就应该一致。
• 容量损失（Capacity Loss）​​：鼓励神经表征具有尽可能高的容量，即最大化能唯一编码的空间位置数量。这与传统信息论中最大化熵的直觉相反，但论文认为这有助于提高表征的效率和泛化能力。 （思考：如果仅通过一个足够大的spacing的module以覆盖整个环境来编码，固然可以表征所有位置，但因为spacing大，同时也需要更多cell才能充分覆盖整个环境；如果加上capcacity loss，就能促进multi module的形成，但当表征过于密集时就很容易产生non local error，这大概就是需要Separation+Capacity这样的组合互相对抗；同时grid的疏密其实也和具体任务中的速度步长、需要表征环境的疏密有关系？如果环境中的位置本身就是很松散的，其实只用大spacing的grid module也是足够的。但最终形成怎样的module才能保证效率最大化呢？why文中一定是出现3个?）
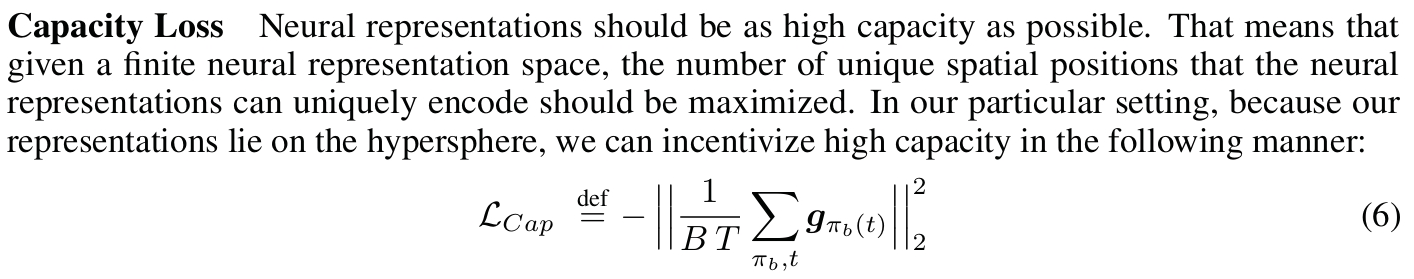
• ​​共形等距损失（Conformal Isometry Loss）​​：确保神经代码的变化与物理速度的大小保持恒定比例，有助于维持空间度量的准确性。

6 Experimental Results

6.1 Emergence of multiple modules of periodic cells

6.2 Generalization to input trajectory statistics

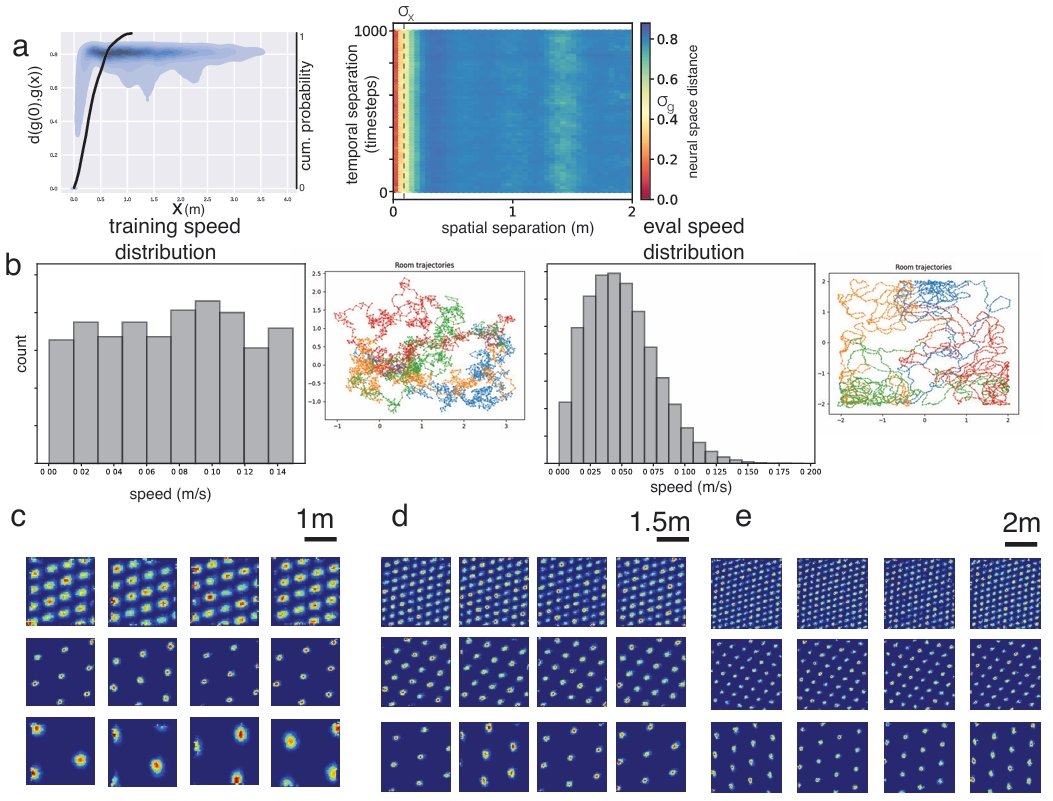
Figure 5: Grid tuning generalizes to different velocity statistics and to environments much larger than the training environment.

（？从separation loss学到的泛化性

6.3 State space analysis of trained RNNs

Figure 6 :Analysis of low-dimensional structure in one of the grid cell modules

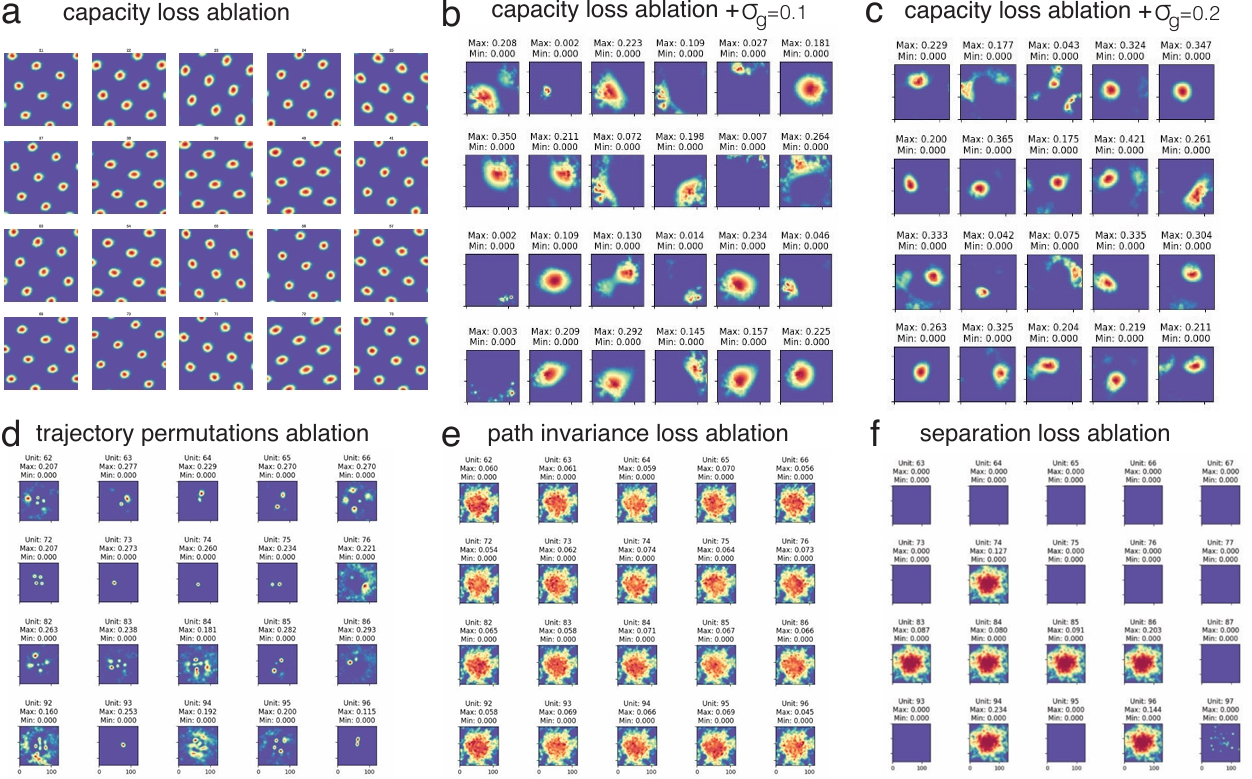
Figure 7: Ablation experiments: (a) Removal of capacity loss leads to a single module of grid cells. (b-c) Reducing σg makes the representation place cell-like, with size of place fields decreasing with increasing σg. (d-f) Ablating other key ingredients leads to loss of spatial tuning.

（可借鉴a，强制g学习multi module; d，进行数据增强、同时得和path invariance结合？

7 Discussion & Future Directions

1) understand these trained recurrent networks and connect them back to grid cells:  What components of the data, augmentations, losses and architecture control the number of modules, the distribution of the module periods, the period ratios, the structure (square or hexagonal) of the lattices? What do the state spaces of these networks look like? Can we reverse-engineer the learnt mechanisms, using mechanistic analyses?

2) what underlying connectivity leads to discrete modular responses: How do the learnt representations change when exposed to experimental manipulations, e.g., environmental deformations or rewards? What new experiments can these networks suggest in biological agents? How might our grid cell recurrent networks, and more generally, SSL principles be applied to drive computational neuroscience forward?

3) push our SIC framework further towards machine learning.

4) one puzzling aspect of our capacity loss is that it can be viewed as minimizing the entropy of the neural representations in representation space, which flies against common information theoretic intuition arguing for maximizing the entropy of the representations. In some sense, the capacity loss is akin to a “dual\" minimum description length problem: instead of maximizing compression by having a fixed amount of unique data and trying to minimize the code words’ length, here we maximize compression by having fixed length code words and trying to maximize the amount of unique data. How can this apparent contradiction be resolved?

Appendix

A Experimental Details

Architecture and training data + augmentations

（why没给isometry loss的比重？

code availability: 部分在rebuttal时提供的代码： https://drive.google.com/drive/folders/1JNmdeTpJhktOoFJ-slC1l2AIqRSw3sAk

ssl计算密集型：16GB GPU ~7 days

B All Ratemaps

Figure 9: All 128 ratemaps evaluated on trajectories inside a 2m box. (a) Ratemaps from the corresponding to Fig. 4 (b) Ratemaps corresponding to the run in Fig.7a (ablation capacity loss)

（看着a图有的module的细胞数也不多嘛？

C Construction of the grid code

D Nonlinear Dimensionality Reduction

PCA (6d) + non-linear dimensionality (spectral embedding 3d)

For Fig. 6, we qualitatively followed the methodology used by seminal experimental papers examining the topology of neural representations [12, 23]: we used principal components analysis to 6 dimensions followed by a non-linear dimensionality (in our case, spectral embedding) reduction to 3 dimensions. Similar results are obtained if one uses Isomap [59].

words

bizarre 离奇的        peculiar 奇特的、特有的

data augmentation 数据增强

N-dimensional sphere N维球体

i.i.d. = Independent Identically Distribution 独立同分布