ShaderGraph节点解析(四十四):4x4 矩阵节点(Matrix 4x4 Node)详解_unity matrix4x4
目录
一、节点功能概述
二、端口与参数详解
2.1 端口配置
2.2 控制参数
三、技术原理解析
3.1 矩阵基础概念
3.2 典型矩阵示例
3.2.1 单位矩阵
3.2.2 旋转矩阵(绕 Z 轴旋转 θ 角)
3.2.3 缩放矩阵
四、应用场景与实战案例
4.1 坐标空间转换
场景:切线空间到世界空间转换
4.2 顶点变换效果
场景:自定义顶点扭曲动画
4.3 投影映射
场景:将纹理投影到物体表面
五、使用技巧与注意事项
5.1 矩阵运算策略
5.2 与其他节点配合
1. 与向量节点配合
2. 与材质属性配合
5.3 性能优化
六、总结与拓展应用
一、节点功能概述
4x4 矩阵节点(Matrix 4x4 Node)是 Unity Shader Graph 中用于定义常量 4x4 矩阵的基础工具。作为线性代数运算的核心组件,该节点允许开发者在 Shader 中直接声明固定矩阵值,用于坐标空间转换、顶点变换和复杂数学运算。其核心优势在于:
- 空间变换基础:支持模型、视图、投影等坐标空间的矩阵定义
- 灵活性高:可自定义任意 4x4 矩阵,满足旋转、缩放、平移等变换需求
- 性能高效:常量矩阵在编译时确定,无运行时计算开销
二、端口与参数详解
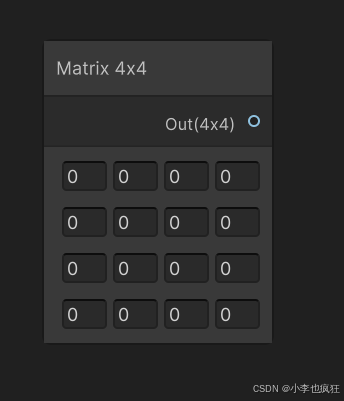
2.1 端口配置
2.2 控制参数
三、技术原理解析
3.1 矩阵基础概念
4x4 矩阵在图形学中主要用于齐次坐标变换,其数学形式为:
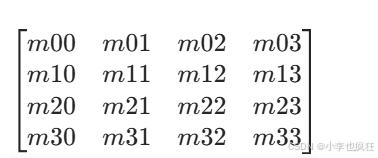
关键用途:
- 线性变换:旋转、缩放、错切等
- 仿射变换:包含平移的复合变换(通过第四列实现)
- 坐标空间转换:如模型到世界、世界到视图的矩阵转换
3.2 典型矩阵示例
3.2.1 单位矩阵
生成代码示例:
hlsl
float4x4 _Matrix4x4 = float4x4( 1, 0, 0, 0, // 第一行:X轴基向量 0, 1, 0, 0, // 第二行:Y轴基向量 0, 0, 1, 0, // 第三行:Z轴基向量 0, 0, 0, 1 // 第四行:平移分量);特性:对向量无变换作用,常用于矩阵初始化
3.2.2 旋转矩阵(绕 Z 轴旋转 θ 角)
hlsl
float theta = _RotationAngle;float4x4 rotationMatrix = float4x4( cos(theta), -sin(theta), 0, 0, sin(theta), cos(theta), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1);3.2.3 缩放矩阵
hlsl
float3 scale = float3(_ScaleX, _ScaleY, _ScaleZ);float4x4 scaleMatrix = float4x4( scale.x, 0, 0, 0, 0, scale.y, 0, 0, 0, 0, scale.z, 0, 0, 0, 0, 1);四、应用场景与实战案例
4.1 坐标空间转换
场景:切线空间到世界空间转换
- 需求:将切线空间法线转换为世界空间
- 实现:
hlsl
// 定义切线空间到世界空间的转换矩阵(假设已通过顶点数据构建)float4x4 tangentToWorld = Matrix4x4Node.Out;// 切线空间法线float3 tangentNormal = float3(0, 0, 1);// 转换到世界空间float3 worldNormal = mul(tangentToWorld, float4(tangentNormal, 0)).xyz;
4.2 顶点变换效果
场景:自定义顶点扭曲动画
- 步骤:
hlsl
// 定义顶点变换矩阵(包含旋转和平移)float4x4 transformMatrix = Matrix4x4Node.Out;// 原始顶点坐标(对象空间)float4 objectVertex = float4(vertex, 1);// 应用变换float4 transformedVertex = mul(transformMatrix, objectVertex);
4.3 投影映射
场景:将纹理投影到物体表面
- 实现:
hlsl
// 定义投影矩阵(假设已计算投影参数)float4x4 projectionMatrix = Matrix4x4Node.Out;// 世界空间顶点坐标float4 worldVertex = mul(unity_ObjectToWorld, float4(vertex, 1));// 计算投影UVfloat4 projectedUV = mul(projectionMatrix, worldVertex);projectedUV.xy /= projectedUV.w; // 归一化
五、使用技巧与注意事项
5.1 矩阵运算策略
5.2 与其他节点配合
1. 与向量节点配合
hlsl
float4x4 matrix = Matrix4x4Node.Out;float3 vector = Vector3Node.Out;float3 transformedVector = mul(matrix, float4(vector, 0)).xyz;2. 与材质属性配合
hlsl
float4x4 scaleMatrix = float4x4( _Scale.x, 0, 0, 0, 0, _Scale.y, 0, 0, 0, 0, _Scale.z, 0, 0, 0, 0, 1);5.3 性能优化
- 避免冗余矩阵: 合并多个小矩阵为一个大矩阵,减少乘法运算次数
- 行主序与列主序: 确保矩阵定义与 HLSL 的行主序一致(默认行优先)
- 移动端优化: 简化复杂矩阵运算,使用半精度浮点存储
六、总结与拓展应用
4x4 矩阵节点作为 Shader 中的数学基础工具,其核心价值在于:
- 空间变换核心:支撑所有坐标系统的转换与顶点变换
- 算法基础:为投影、变形等复杂效果提供数学载体
- 灵活性保障:自定义矩阵满足各种创意性数学需求
拓展方向:
- 结合矩阵节点实现自定义相机投影效果
- 在 VR 中利用矩阵运算优化空间定位与交互
- 开发基于矩阵的程序性建模算法,动态生成复杂几何


