系统学习算法：动态规划（简单多状态dp）_动态规划算法状态方程

题目一：

思路：

这道题是比较经典的简单多状态dp，什么是多状态dp呢，先不着急，分析完这道题就知道了

题意非常简单，就是不能连着偷，必须隔开偷，但可以隔好几个，反正最少隔1个，要求最后偷的金额最高

算法原理：

不管是什么，只要是动态规划，就还是五步

1.状态表示

根据经验和题目要求，我们可以设为以i位置为结尾，所偷窃的最高金额

这里其实还不够细节，因为有偷和不偷两种选择

要么是以i位置为结尾，偷该位置所偷窃的最高金额

要么是以i位置为结尾，不偷该位置所偷窃的最高金额

所以这就出现了多状态dp，那么解决办法就是开两个dp表，f表示偷，g表示不偷（取名fg的原因是数学中f（x）和g（x）函数）

2.状态转移方程

因为有两个dp表，所以每个dp表的状态转移方程都不一样

f表中表示当前位置偷，那么前一个位置就不能偷，而g表又代表不能偷的最高金额，所以状态转移方程为

f [ i ] = g [ i ] +nums[ i ]

g表中表示当前位置不偷，那么前一个位置可以偷，也可以不偷，因为要表示不偷当前位置的最高金额，所以要选前一个位置的最高金额，因此状态转移方程为

g [ i ] = Math.max( f[ i - 1 ]，g[ i - 1 ] )；

3.初始化

假设从第一个房子开始偷，那么如果偷，那么就是第一个房子的金额，因此f[0]=nums[0]

如果不偷，那么就是0，g[0]=0

4.填表顺序

根据状态表示，当前位置的状态由前面的状态决定，所以从左往右填

5.返回值

偷到最后一个房子时，有可能偷该房子，也有可能不偷该房子，选两个dp表最高金额的返回即可

代码：

class Solution { public int rob(int[] nums) { int len=nums.length; //初始化（f表示选，g表示不选） int[] f=new int[len]; int[] g=new int[len]; f[0]=nums[0]; g[0]=0; //状态转移方程 for(int i=1;ig[len-1]?f[len-1]:g[len-1]; }}

题目二：

思路：

跟上一道题几乎一模一样，就是多了一个条件，那就是首尾是相连的，从单向线性变成了一个环形

算法原理：

还是从第一个房子偷和不偷开始讨论

如果偷，那么第二个房子和最后一个房子不能偷，但是第三个房子到倒数第二个房子就跟上一道题正常偷

如果不偷，那么第二个房子到最后一个房子都能按照上一题正常偷

也就是通过分类讨论，将环形问题转化为两个线性的打家劫舍

那么剩下的五步分析就跟第一题几乎一模一样了，至少初始化的位置和返回值不一样，以及当房子数偏小，不足以分划区间时，进行特判

代码：

class Solution { public int rob(int[] nums) { //特判一下 int n=nums.length; if(n<=3){ int max=0; for(int x:nums){ max=Math.max(max,x); } return max; } //初始化 int[] f1=new int[n]; int[] g1=new int[n]; int[] f2=new int[n]; int[] g2=new int[n]; //第一个不偷 f1[1]=nums[1]; g1[1]=0; for(int i=2;i<n;i++){ f1[i]=g1[i-1]+nums[i]; g1[i]=Math.max(f1[i-1],g1[i-1]); } int ret1=Math.max(f1[n-1],g1[n-1]); //第一个偷 f2[2]=nums[2]; g2[2]=0; for(int i=2;i<n-1;i++){ f2[i]=g2[i-1]+nums[i]; g2[i]=Math.max(f2[i-1],g2[i-1]); } int ret2=Math.max(f2[n-2],g2[n-2])+nums[0]; return Math.max(ret1,ret2); }}

题目三：

思路：

跟打家劫舍的问题差不多，也是选择一个点数，然后相邻的数不能选，求最后选出来的最大值是多少，主要区别是这里的数有可能不是连续的，也就是说有可能位置是相邻的，但数不是相邻的，那么还是可以选

算法原理：

和打家劫舍问题非常相似，只是有稍微的区别，算法中有一种方法就是通过预处理，将题型转变为熟悉的题型，我们打家劫舍问题非常熟悉，所以我们现在思考能不能将这道题通过预处理来转化为打家劫舍

既然唯一的区别就是在位置上有不同，打家劫舍是以下标为位置，这道题是以数字为位置，那么我们将数字转变为下标就可以了

 这时经过上图的预处理，对arr进行一次打家劫舍就解决了

主要难点在于如何将题型转化，剩下的动态规划步骤跟打家劫舍问题一模一样，就不多说了，反正还是五个步骤

代码：

class Solution { public int deleteAndEarn(int[] nums) { //预处理 int n=0; for(int x:nums){ n=Math.max(n,x); } int[] arr=new int[n+1]; for(int x:nums){ arr[x]+=x; } //打家劫舍问题 int[] f=new int[n+1]; int[] g=new int[n+1]; f[1]=arr[1]; g[1]=0; for(int i=2;i<n+1;i++){ f[i]=g[i-1]+arr[i]; g[i]=Math.max(f[i-1],g[i-1]); } return Math.max(f[n],g[n]); }}

题目四：

思路：

还是跟打家劫舍差不多，也是相邻之间不能颜色相同，但是不是选择偷不偷了，而是选择颜色，且有三种颜色可选，行代表第几个房子，列表示刷颜色的成本，0为红色，1为蓝色，2为绿色，然后返回最少成本

其实写到这里简单多状态dp问题的题特征很明显了，那就是每次有多种选择，且选择与之前或之后的操作有关联，因此我们可以想到采用什么算法来解决

算法原理：

还是五步

1.状态表示

根据经验加题目要求，就是以i位置为结尾，所需的最少成本 

但还不够细，这也是多状态dp的特点，根据选择因此还要细分为：

以i位置为结尾，选择刷红色的话所需的最少成本

以i位置为结尾，选择刷蓝色的话所需的最少成本 

以i位置为结尾，选择刷绿色的话所需的最少成本

那么就开三个dp表，每个dp表对应一种状态表示

2.状态转移方程

因为相邻不能刷一样的，所以如果当前位置刷红色，那么前面的只能刷蓝色或者绿色，又因为要求最少成本，因此要选择前面蓝色和绿色中的最小值，再加上当前位置刷红色的成本

因此状态转移方程为

r[i]=Math.min(b[i-1],g[i-1])+costs[i][0];

同理，蓝色和绿色一样

b[i]=Math.min(r[i-1],g[i-1])+costs[i][1];

g[i]=Math.min(r[i-1],b[i-1])+costs[i][2];

3.初始化

从第一个房子开始刷，那么三种颜色都可以选，刷哪个颜色就初始化哪个颜色的成本

4.填表顺序

根据前面的房子选择刷的颜色，来决定当前位置刷选什么颜色，所以是根据前面推后面，因此填表顺序为从左到右

5.返回值

刷完最后一个房子，返回到最后一个房子刷三种颜色之间的最小值

代码：

class Solution { public int minCost(int[][] costs) { //初始化 int n=costs.length; //r=red，b=blue，g=green int[] r=new int[n]; int[] b=new int[n]; int[] g=new int[n]; r[0]=costs[0][0]; b[0]=costs[0][1]; g[0]=costs[0][2]; //状态转移方程 for(int i=1;i<n;i++){ r[i]=Math.min(b[i-1],g[i-1])+costs[i][0]; b[i]=Math.min(r[i-1],g[i-1])+costs[i][1]; g[i]=Math.min(r[i-1],b[i-1])+costs[i][2]; } //返回值 return Math.min(r[n-1],Math.min(b[n-1],g[n-1])); }}

当然也可以将三个一维dp表转成一个二维dp表，都可以，但思路都是一样的 

题目五：

思路：

股票问题算是多状态dp中的一个子类别，也是存在多种选择，这道题就是买入，卖出，冷冻期三种选择，以示例1为例，很容易明白题意，就是通过各种操作，返回最后最大利润，还有一点，如示例二，不是说像现实能无限期持有，而是在数组长度的天数内赚取更多的利润，所以可以啥也不干，这也是一个隐藏的选择，就是你不一定每天都要有操作，也可以啥也不干

算法原理：

还是五步

1.状态表示

根据经验和题目要求，就是以第i天为结尾，所赚取的最大利润，而这个不够细，还可细分为多种子状态，其中买入和卖出这个状态是瞬间的，而冷冻期和啥也不干是持久的，所以我们稍微分类一下，就是将卖出前归为“持有”状态，将买入前和啥也不干归为“可交易”状态，冷冻期为单独的一种状态，因此可以创建三个dp表分别表示三种状态

2.状态转移方程

像这种分析起来比较复杂，每种状态转化情况非常多的话，可以借助“状态机”的方法，这个方法对于多状态分析非常好用，简单来说就是画出三种状态的完全有向图

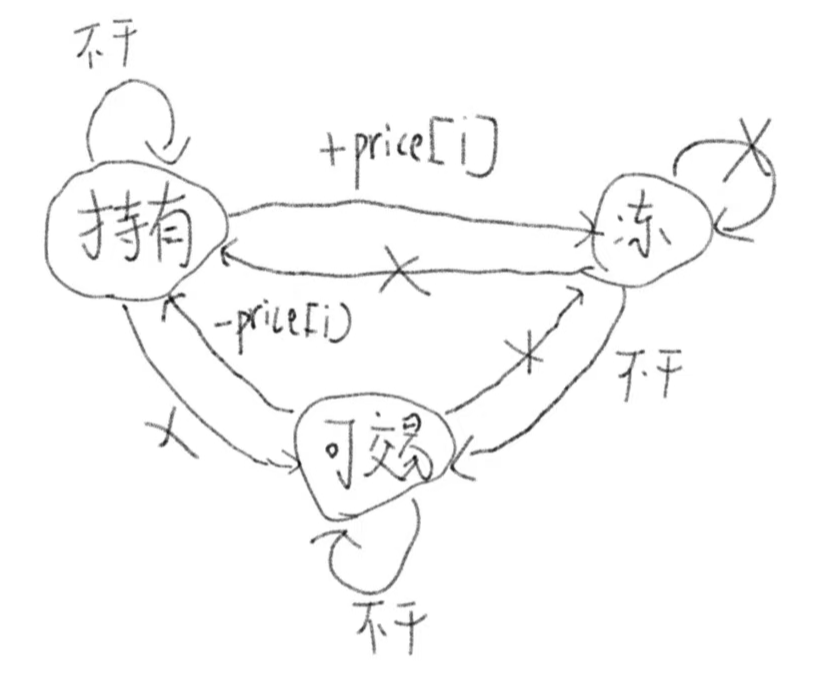
这样子不仅不会漏情况，并且非常直观，对上图分析一下

首先先对持有状态进行分析：

前一天的持有状态能到当天的持有状态吗，可以的，只需要前一天啥也不干，所以自身能到自身

前一天的可交易状态能到当前的持有状态吗，可以的，只需要前一天买了股票，就能变为持有状态

前一天的冷冻期状态能到当前的持有状态吗，不能，因为冷冻期不能进行买入操作，不能转变

然后再对可交易状态进行分析：

前一天的可交易状态能到当前的可交易状态吗，可以，只需要前一天啥也不干，所以自身能到自身

前一天的持有状态能到当天的可交易状态吗，不能，因为中间需要间隔一天冷冻期，不能转变

前一天的冷冻期状态能到当天的可交易状态吗，可以，只需等冷冻期解冻，就变为可交易状态了

最后再对冷冻期进行分析：

前一天的冷冻期状态能到当天的冷冻期状态吗，不能，因为冷冻期只有一天，不能自身到自身

前一天的持有状态能到当天的冷冻期状态吗，可以，只需要卖掉股票就行，所以可以转变

前一天的可交易状态能到当天的冷冻期状态吗，不能，只有卖股票才能进入冷冻期，不能转变

通过上面的分析，就能画出上面的完全有向图

然后再排除掉不能转变的箭头，剩下的就是状态转移方程，又因为是找最大利润，所以取max

所以状态转移方程为

 //持有状态 have[i]=Math.max(have[i-1],can[i-1]-prices[i]); //可交易状态 can[i]=Math.max(can[i-1],cold[i-1]); //冷冻期状态 cold[i]=have[i-1]+prices[i];

3.初始化

那就是第一天的情况，第一天如果为持有状态，那么就是买入股票，利润为-price[0]

如果为可交易状态，那么就是啥也不干，利润为0

如果为冷冻期状态，那就是当天买当天卖，瞎忙活，利润为0

4.填表顺序

因为当前的情况由前一天的情况决定，所以填表顺序为从左到右

5.返回值

那就是返回最后一天三种状态的最大值即可，其中持有状态一定不可能是答案，因为它最后比另外两种状态多亏了持有股票的价值，所以完全可以只比较可交易状态和冷冻期状态，当然如果加进来也无所谓，反正也会被排除掉

代码：

class Solution { public int maxProfit(int[] prices) { //初始化 int n=prices.length; int[] have=new int[n]; int[] can=new int[n]; int[] cold=new int[n]; have[0]=-prices[0]; can[0]=0; cold[0]=0; //状态转移方程 for(int i=1;i<n;i++){ //持有状态 have[i]=Math.max(have[i-1],can[i-1]-prices[i]); //可交易状态 can[i]=Math.max(can[i-1],cold[i-1]); //冷冻期状态 cold[i]=have[i-1]+prices[i]; } //返回值 return Math.max(can[n-1],cold[n-1]); }}

题目六：

思路：

还是股票问题，跟上一题差不多，区别是这一题没有冷冻期，但多了每次交易会交一次手续费，最后返回最大利润

算法原理：

还是五步

1.状态表示

根据经验加题目要求，那就是以第i天为结尾，最大利润，但是不够细，因为有两种选择：买入和卖出，所以还可以细分，因为买入和卖出为瞬间动词，与状态这种持续的不是很贴切，于是我们换个词来形容，买入——持有，卖出——可交易

 以第i天以持有状态为结尾，最大利润

以第i天以可交易状态为结尾，最大利润

所以开两个dp表来表示就行

2.状态转移方程

如果对多状态的转移觉得很杂乱，可以画“状态机”来帮助，非常清晰

从前一天持有到当天持有，只需要啥也不干就行

从前一天可交易到当天持有，只需要买入当天股票就行

从前一天持有到当天可交易，只需要卖出股票并支付手续费就行

从前一天可交易到当天可交易，只需要啥也不干就行

根据上面的分析画出完全有向图，就可以根据这个来写出状态转移方程了

又因为是要找最大利润，那就是取max

 have[i]=Math.max(have[i-1],can[i-1]-prices[i]); can[i]=Math.max(can[i-1],have[i-1]+prices[i]-fee);

 3.初始化

为了避免i-1越界，所以要初始化，第1天如果是持有状态那就是买入股票为-price[0]，如果可交易状态就是啥也不干为0

4.填表顺序

当天状态根据前一天的状态决定，所以从左往右

5.返回值

如果最后一天还是持有股票不卖，那肯定比当初不买的利润低，所以直接返回最后一天可交易状态的dp值就行

代码：

class Solution { public int maxProfit(int[] prices, int fee) { //初始化 int n=prices.length; int[] have=new int[n]; int[] can=new int[n]; have[0]=-prices[0]; can[0]=0; //状态转移方程 for(int i=1;i<n;i++){ have[i]=Math.max(have[i-1],can[i-1]-prices[i]); can[i]=Math.max(can[i-1],have[i-1]+prices[i]-fee); } //返回值 return can[n-1]; }}

题目七：

思路：

这道题也是股票问题，跟之前的区别是这道题是有交易次数限制，其中最多交易次数为2，需要注意的是最多。而不是必须，也就是说可以交易0次，1次，不是必须完成2次交易

算法原理：

还是五步

1.状态表示

依旧多状态，所以一开始以第i天为结尾，最多利润不够细，因为有买入卖出两种选择，所以还可以细分为第i天为持有状态为结尾，最多利润，第i天为可交易状态为结尾，最多利润，但是还不够细，因为这道题还有交易次数，可以选择0，1，2次，因此还可以细分为

第i天为持有状态为结尾，此时交易次数为0，最多利润

第i天为持有状态为结尾，此时交易次数为1，最多利润

……

因此我们可以用两个二维dp表，分别表示持有和可交易状态，然后第一维表示第i天，第二维表示为第 j 次交易，当然也可以创建一个三维dp表，将第三维表示持有和可交易状态，都是一样的，所以如果发现状态表示还不够细时，要么就是创建多个dp表，要么就升维，直到能够清楚表示每种状态为止

2.状态转移方程

还是先画“状态机”

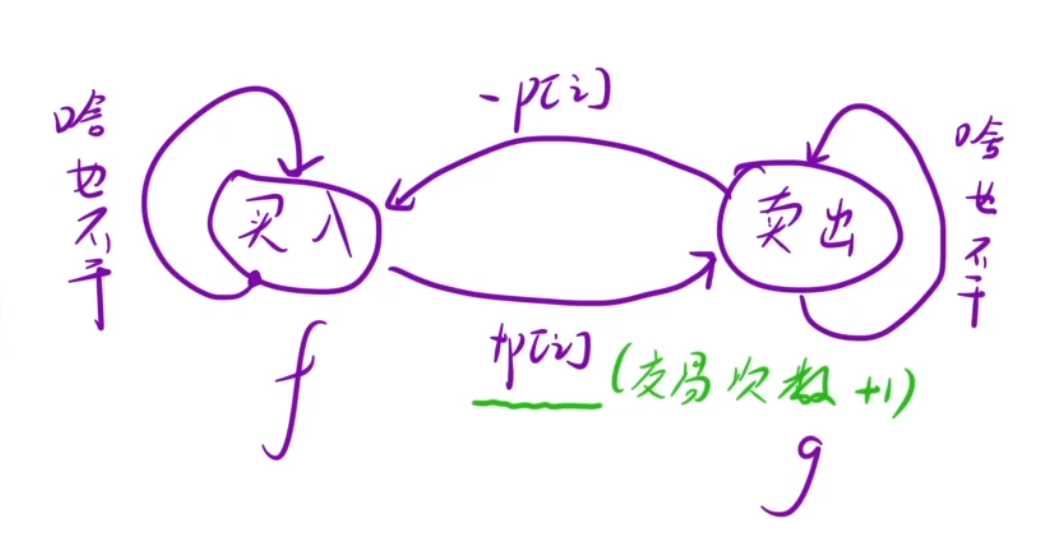
能转化为当天持有状态的有：

前一天持有状态啥也不干和前一天可交易状态通过购买股票

又因为要最大利润，所以取max

还因为加入了交易次数，而只有当买了再卖了才算完成一次交易，所以在购买的时候，不用管交易次数，原来是多少次就多少次

所以持有状态的状态转移方程为：

have[i][j]=Math.max(have[i-1][j],can[i-1][j]-prices[i]);

能转化为当天可交易状态的有：

前一天可交易状态啥也不干和前一天持有状态通过卖出股票

又因为要最大利润，所以取max

还因为加入了交易次数，而只有当买了再卖了才算完成一次交易，所以在卖出的时候，需要用到上一次交易结束后的利润再加上这一次卖出股票的钱才是这一次交易次数（交易次数加一）结束的利润，也就是

上一次交易结束后的利润+这一次卖出股票的钱=这一次交易次数结束的利润

所以可交易状态的状态转移方程为：

can[i][j]=Math.max(can[i-1][j],have[i-1][j-1]+prices[i]);

3.初始化

目的就是为了防止越界

其中这一题需要注意的点挺多

跟之前一样的是第0天时，处于持有状态的话，就是-price[0]，处于可交易状态的话，那就是0

但是因为这道题有最多交易次数，所以我们要珍惜交易次数，因此所谓的当天买当天卖这种浪费交易次数的行为不可取，因此第0天的第1次交易和第2次交易是不可能存在的，又因为在状态转移方程中取max，为了不让这个影响的结果，所以按理来说是取整数的最小值Integer.MIN_VALUE

但是在买入股票的时候，can[i-1][j]-prices[i]这个式子中，如果can[i-1][j]为最小值，那么再减去一个正整数，就发生了越界，在不同语言中，有的会报错，有的会直接转化为正数，所以初始化为Integer.MIN_VALUE不合理，这里就有一个算法常用的知识，那就是会初始化为-0x3f3f3f3f（十六进制），这个十六进制数就是Integer.MIN_VALUE的一半，它足够小，对于所有算法题来说基本都是，又不会越界，反之，如果有最大值，如果为了避免越界，往往不会使用Integer.MAX_VALUE而是0x3f3f3f3f，算是一个技巧

然后还有一个地方会发生越界，就是have[i-1][j-1]+prices[i]，当j=0时，j-1就越界了，之前解决办法是多开一行多开一列，这里没必要，有一个新办法就是加个if判断就好了，当j-1>=0时才取max，反之就只有can[i-1][j]这一种转化情况

4.填表顺序

还是从上往下，从左往右

5.返回值

因为可交易状态绝对比持有状态利润大，所以只用在可交易状态中找，那就是最后一天中，交易0，1，2次哪次交易总数最大

代码：

class Solution { public int maxProfit(int[] prices) { //初始化 int n=prices.length; int[][] have=new int[n][3]; int[][] can=new int[n][3]; have[0][0]=-prices[0]; have[0][1]=have[0][2]=-0x3f3f3f3f; can[0][0]=0; can[0][1]=can[0][2]=-0x3f3f3f3f; //状态转移方程 for(int i=1;i<n;i++){ for(int j=0;j=0){  can[i][j]=Math.max(can[i-1][j],have[i-1][j-1]+prices[i]); }else{  can[i][j]=can[i-1][j]; } } } //返回值 int ret=can[n-1][0]; for(int j=1;j<3;j++){ if(ret<can[n-1][j]){ ret=can[n-1][j]; } } return ret; }}

题目八：

思路：

 其实跟上一题一模一样，那就是将2笔交易变为k笔交易，从特解转化为通解，那么就对上一题的交易次数从2修改为k就行，套答案就行，分析思路一模一样

代码：

class Solution { public int maxProfit(int k, int[] prices) { //初始化 int n=prices.length; int[][] have=new int[n][k+1]; int[][] can=new int[n][k+1]; have[0][0]=-prices[0]; can[0][0]=0; for(int j=1;j<k+1;j++){ have[0][j]=can[0][j]=-0x3f3f3f3f; } //状态转移方程 for(int i=1;i<n;i++){ for(int j=0;j=0){  can[i][j]=Math.max(can[i-1][j],have[i-1][j-1]+prices[i]); }else{  can[i][j]=can[i-1][j]; } } } //返回值 int ret=can[n-1][0]; for(int j=1;j<k+1;j++){ if(ret<can[n-1][j]){ ret=can[n-1][j]; } } return ret; }}

总结：

所谓的多状态，就是不同选择，而我们要做的就是将一种选择描述清楚，通过添加各种定语来细分，如果某一个定语不够形容，那就再加一个定语，在代码上体现那就是升维或者开多个dp表，然后按照五个步骤解决即可