大模型的开发应用（二十）：AIGC原理_图生模型

这里写目录标题

• 0 前言
• 1 文生图
• • 1.1 最简单的图像生成模型
  • 1.2 DALL·E 2
• 2 Stable Diffusion
• • 2.1 核心模块组成
  • 2.2 文生图工作流程详解
  • 2.3 图生图工作流程详解
  • 2.4 不同的采样方式区别
  • • ⚙️ 一、采样方法的数学本质
    • 🔬 二、主流采样方法分类与公式解析
    • • 📊 1. 基础确定性采样器（收敛型，没有随机噪声）
      • 🎲 2. 随机性采样器（不收敛型）
      • ⚡ 3. 高效多步采样器（平衡型）
      • ⚠️ 4. 淘汰或不推荐采样器
    • 📊 三、关键参数对采样效果的影响
    • 💎 四、总结：选择建议与典型场景
  • 2.5 与 DALL·E 2 的结构对比
  • 2.6 设计优势与局限
  • 2.7 关于 Stable Diffusion 本地部署
  • 2.7 总结

0 前言

上篇文章，我们介绍了AIGC的先修知识，介绍了 ViT、CLIP、VAE 和 Diffusion，这篇文章是在这些个模型的基础上，介绍图像生成模型（包括文生图和图生图），本文将重点介绍 Stable Diffusion 的原理。

1 文生图

1.1 最简单的图像生成模型

VAE 的解码器具有图像生成的功能，但是它需要一个潜空间（Latent Space）向量，如果这个向量能体现输入的文本特征，那么就可以根据这个向量生成图像。此时我们很容易想到文本特征提取器，例如最基础的 Bert，不过这里用 CLIP 中的文本编码器比较合适，因为它提取的特征和图像特征对齐了，也就是说，CLIP 的文本编码器输出的文本特征，可以认为是某张图像的特征，只不过这张图象暂时还没有，需要我们生成。

好的，现在我们可以搭建最简单的文生图模型了，架构如下图所示：

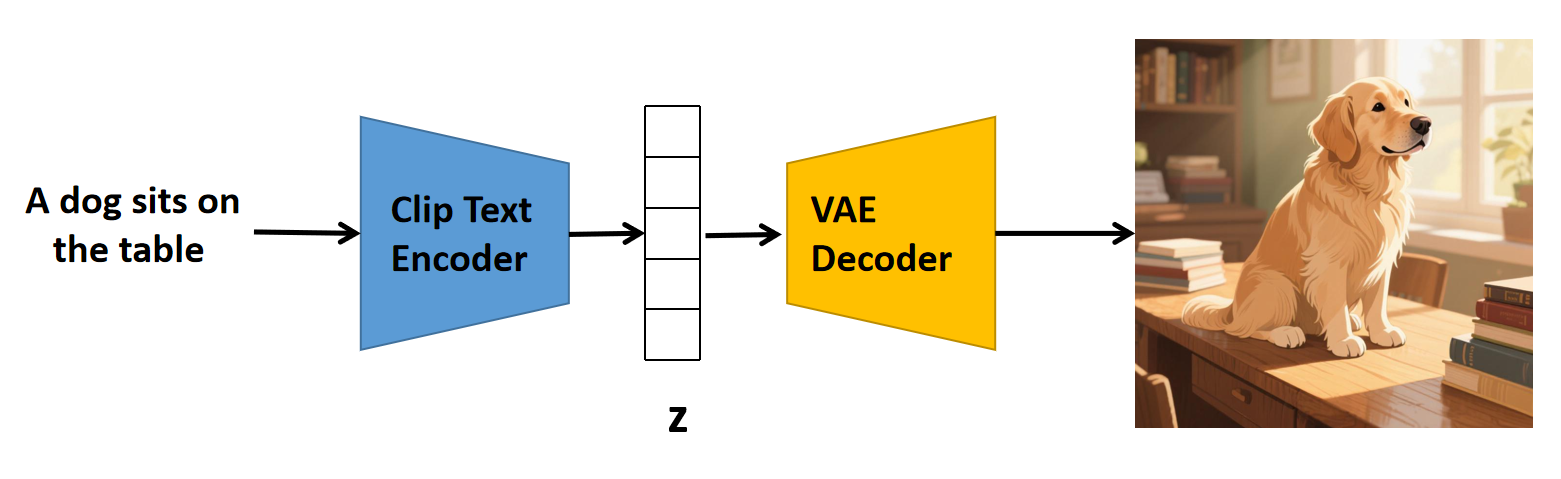
上面的理论模型还是有点问题的，因为 CLIP 的文本编码器输出的特征向量，它并不是某张图片的特征向量，只是两个向量在相同的分量上能同时取得最大值。这个架构只是为了方便理解后续模型用的，没有人真的这么用（或许有，只是我不知道而已），当然，也有可能经过一定的训练后，CLIP的文本编码器也能输出相关图像的特征。

1.2 DALL·E 2

CLIP 的文本编码器与图像编码器，输出的特征向量长度是相同的，并且两者强相关，那么是否可以增加一个转换模型，把文本特征向量转换成图像特征向量？DALL·E 2 模型就是这个 idea 的具体实现。

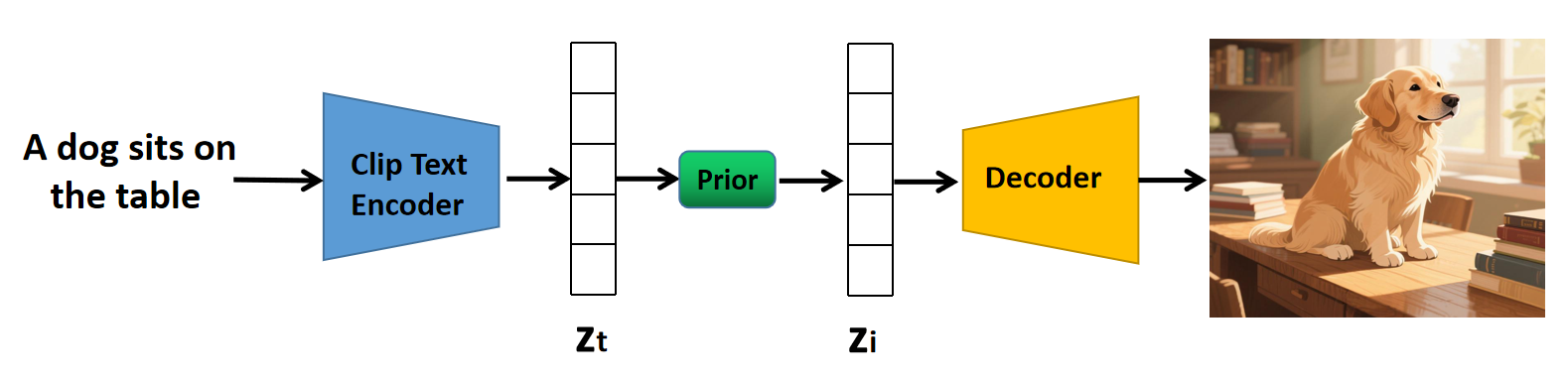
图中， Z t Z_t Zt​ 是从文本中提取的特征，将其输入到 Prior 模块（也称为先验模块）后，得到 Z i Z_i Zi​，它是文本所对应的图像的特征（只是这张图像未必存在），也就是说，起转换作用的是这个先验模块。

Prior 模块也是通过扩散模型实现的，以随机高斯噪声为起点​，用文本特征 Z t Z_t Zt​ 作为条件引导去噪方向，最后得到对应的图像特征。训练的时候，需要把 “文本-图像” 对输入到 CLIP，得到文本特征和图像特征，然后按照训练扩散模型的方式进行训练。这里不做具体展开，只需要知道 Prior 是干什么用的就行了。

训练完 Prior 后，还需要训练 Decoder。训练时使用 CLIP 的图像特征提取器，输入原始图像得到特征，然后将特征输入到 Decoder 得到生成图，计算生成图与原始图的损失函数，进而更新 Decoder 中的参数，训练时同样是冻结 CLIP 的参数。

注意，DALL·E 2 模型的 Decoder，不是 VAE 的 Decoder，而是基于扩散模型的解码器，因为 DALL·E 2 模型并非我们要掌握的重点，所以只需要知道 DALL·E 2 模型的 Decoder 与 VAE 的 Decoder 完成了相同的功能就行。

2 Stable Diffusion

Stable Diffusion（SD）是一种基于潜在扩散模型（Latent Diffusion Model, LDM） 的文本到图像生成架构，其核心设计通过将高维像素空间压缩到低维潜空间，显著降低了计算复杂度。以下是其详细结构及工作流程：

2.1 核心模块组成

Stable Diffusion 包含三个核心模块，协同完成从文本到图像的生成过程：

1. CLIP 文本编码器（Text Encoder）

   • 功能：将输入的自然语言描述（Prompt）转换为语义向量（Text Embedding）。
   • 实现：使用预训练的 CLIP 模型的文本编码部分，输出维度为 [B, K, E]（B为批大小，K为最大文本长度，E为嵌入维度）。
   • 作用：提供生成图像的语义指导条件。

2. U-Net 扩散网络（Diffusion Model）

   • 功能：在潜空间执行迭代去噪，生成包含语义信息的潜变量。
   • 结构：
     • Encoder-Decoder 架构：包含下采样（压缩特征）和上采样（恢复细节）层。
     • 条件注入机制：
       • 时间步嵌入（Timestep Embedding）：控制不同去噪阶段的强度。
       • 空间变换器（Spatial Transformer）：通过交叉注意力（Cross-Attention）将文本嵌入与图像特征融合。其中，图像特征作为 Query，文本嵌入作为 Key/Value，实现图文语义对齐。
     • 跳跃连接（Skip Connections）：保留底层细节，避免信息丢失。
   • 输入/输出：输入为带噪潜变量（维度 [B, Z, H/8, W/8]），输出为去噪后的潜变量（同维度）。

3. 变分自编码器（VAE）

   • 编码器（Encoder）：将原始图像（如 512×512×3）压缩到低维潜空间（如 64×64×4），降维至 1/8 分辨率。
   • 解码器（Decoder）：将去噪后的潜变量解码为像素级图像（如 512×512×3）。
   • 意义：大幅减少扩散过程的计算量（潜空间比像素空间小 64 倍）。

2.2 文生图工作流程详解

Stable Diffusion 的生成过程分为三个阶段（文生图）：

1. 文本编码（Text Encoding）

   • 输入提示词（如 “a cat on a sofa”）经 CLIP 编码为语义向量 z t e x t z_{text} ztext​。

2. 潜空间扩散与去噪（Latent Diffusion）

   • 初始化：从高斯噪声采样生成初始潜变量 x n o i s e x_{noise} xnoise​（维度 64×64×4），它也是 x T x_T xT​。
   • 迭代去噪：

     • 条件注入：U-Net 结合文本嵌入 z t e x t z_{text} ztext​ 和时间步信息，预测当前步的噪声 ϵ θ ( x t , t , z t e x t ) \\epsilon_\\theta(x_t, t, z_{text}) ϵθ​(xt​,t,ztext​)。

     • 去噪更新：通过采样器（如 DDIM、PLMS）逐步更新潜变量，公式简化如下：
       x t − 1 = 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t , z t e x t ) ) + σ t z x_{t-1} = \\frac{1}{\\sqrt{\\alpha_t}} \\left( x_t - \\frac{1 - \\alpha_t}{\\sqrt{1 - \\bar{\\alpha}_t}} \\epsilon_\\theta(x_t, t, z_{text}) \\right) + \\sigma_t z xt−1​=αt​ ​1​(xt​−1−αˉt​ ​1−αt​​ϵθ​(xt​,t,ztext​))+σt​z

       参数说明：

       • x t x_t xt​：当前时间步 $t$ 的带噪图像（潜变量）。
       • ϵ θ \\epsilon_\\theta ϵθ​：U-Net 预测的噪声（模型输出）。
       • α t \\alpha_t αt​：噪声调度参数，控制当前步的噪声强度（ 0 < α t < 1 0 < \\alpha_t < 1 0<αt​<1），由噪声调度策略计算得到，属于模型预配置的一部分。
       • α ˉ t \\bar{\\alpha}_t αˉt​：累积噪声调度参数，定义为 α ˉ t = ∏ i = 1 t α i \\bar{\\alpha}_t = \\prod_{i=1}^{t} \\alpha_i αˉt​=∏i=1t​αi​。
       • σ t \\sigma_t σt​：随机噪声的方差，通常取 σ t = ( 1 − α t) ( 1 − α ˉ t − 1 ) / ( 1 − α ˉ t) \\sigma_t = \\sqrt{(1 - \\alpha_t)(1 - \\bar{\\alpha}_{t-1})/(1 - \\bar{\\alpha}_t)} σt​=(1−αt​)(1−αˉt−1​)/(1−αˉt​) ​，也可以取 1 − α t \\sqrt{1 - \\alpha_t} 1−αt​ ​。
       • ε θ ε_θ εθ​ 为 U-Net 预测的噪声。
       • $z$：标准高斯噪声 $z\sim \mathcal{N}(0,I)$，引入随机性。

     • 迭代次数：通常 20-50 步（远少于像素级扩散模型的 1000 步）。

3. 图像重建（Image Decoding）

   • 去噪后的潜变量 x 0 x_0 x0​ 输入 VAE Decoder，生成最终图像（512×512），过程为：将 x 0 x_0 x0​ 展平成一位向量、全连接升维、重塑特征图为三维张量、转置卷积上采样。过程示意图如下：

4. 过程示意图

#mermaid-svg-Cx18dJ0Bm5OFuAKt {font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .error-icon{fill:#552222;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .marker{fill:#333333;stroke:#333333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .marker.cross{stroke:#333333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt svg{font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .label{font-family:\"trebuchet ms\",verdana,arial,sans-serif;color:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .cluster-label text{fill:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .cluster-label span{color:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .label text,#mermaid-svg-Cx18dJ0Bm5OFuAKt span{fill:#333;color:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .node rect,#mermaid-svg-Cx18dJ0Bm5OFuAKt .node circle,#mermaid-svg-Cx18dJ0Bm5OFuAKt .node ellipse,#mermaid-svg-Cx18dJ0Bm5OFuAKt .node polygon,#mermaid-svg-Cx18dJ0Bm5OFuAKt .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .node .label{text-align:center;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .node.clickable{cursor:pointer;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .arrowheadPath{fill:#333333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .cluster text{fill:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt .cluster span{color:#333;}#mermaid-svg-Cx18dJ0Bm5OFuAKt div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-Cx18dJ0Bm5OFuAKt :root{--mermaid-font-family:\"trebuchet ms\",verdana,arial,sans-serif;} 输入文本 CLIP 文本编码器 生成文本嵌入 z_text 随机高斯噪声 U-Net 扩散模型 迭代去噪生成潜变量 z_0 VAE 解码器 输出高清图像

2.3 图生图工作流程详解

在 Stable Diffusion 中，​图生图（img2img）与文生图（txt2img）共享同一个 U-Net 模型和噪声调度参数 α t \\alpha_t αt​，但两者的输入初始化方式和部分参数逻辑存在差异。尽管模型和调度参数相同，两种模式在 ​输入构造​ 和 ​噪声强度控制​ 上存在显著区别。

图生图模式中，原图通过 ​VAE 编码器压缩为潜变量 z 0 z_0 z0​，根据重绘强度​（如 0.3）计算 α ˉ t \\bar{\\alpha}_t αˉt​：
α ˉ t = ( 1 − s ) 2 \\bar{\\alpha}_t=(1-s)^2 αˉt​=(1−s)2
$s$ 是重绘强度，s 越大，生成结果越偏离原图。若 s 为1，则 x t \\mathbf{x}_t xt​ 完全服从标准正太分布，整个过程和文生图没差，若 s 为0，则完全保留原图（无噪声添加）。

接下来是生成混合噪声：
x t = α ˉ t x 0 + 1 − α ˉ t ϵ , ϵ ∼ N ( 0 , I ) \\mathbf{x}_t = \\sqrt{\\bar{\\alpha}_t} \\mathbf{x}_0 + \\sqrt{1-\\bar{\\alpha}_t} \\boldsymbol{\\epsilon}, \\boldsymbol{\\epsilon} \\sim \\mathcal{N}(0, \\mathbf{I}) xt​=αˉt​ ​x0​+1−αˉt​ ​ϵ,ϵ∼N(0,I)
x t \\mathbf{x}_t xt​ 就是输入到 U-Net 模型中的初始潜变量，迭代去噪的步数由用户指定，过程和文生图的时候一致。

重绘强度 s 的设置：若是微调图像细节（如修复面部、调色），则 0.2-0.4 ；若是风格转换（如照片转油画），则 0.5-0.7 ；若是创意重构（如更换主体内容），则 0.8~1.0。

2.4 不同的采样方式区别

所谓采样方式，指的是根据 x t x_{t} xt​ 得到 x t − 1 x_{t-1} xt−1​ 的方式，采样过程输出的最终潜变量是 x 0 x_0 x0​，将其输入到 VAE Decoder 用于图像解码。

Stable Diffusion 中的采样方法（Sampler）是控制图像生成过程中潜变量迭代更新策略的核心组件，其数学本质是通过数值求解扩散逆过程，逐步将带噪潜变量 z t z_t zt​ （即前面的 x t x_{t} xt​）更新为更去噪的状态 z t − 1 z_{t-1} zt−1​（即前面的 x t − 1 x_{t-1} xt−1​）。以下是常见采样方法的分类、公式解析及特点对比：

⚙️ 一、采样方法的数学本质

所有采样方法均基于以下通用更新公式：
z t − 1= 1 α t ( z t − 1 − α t 1 −α ˉ t ϵ θ ( z t , t ) ) + σ t ϵ z_{t-1} = \\frac{1}{\\sqrt{\\alpha_t}} \\left( z_t - \\frac{1 - \\alpha_t}{\\sqrt{1 - \\bar{\\alpha}_t}} \\epsilon_\\theta(z_t, t) \\right) + \\sigma_t \\epsilon zt−1​=αt​ ​1​(zt​−1−αˉt​ ​1−αt​​ϵθ​(zt​,t))+σt​ϵ

• ϵ θ ( z t , t ) \\epsilon_\\theta(z_t, t) ϵθ​(zt​,t): U-Net 预测的噪声残差（受时间步 $t$ 和文本条件控制）
• α t , α ˉ t \\alpha_t, \\bar{\\alpha}_t αt​,αˉt​: 噪声调度器定义的信号保留系数 α ˉ t = ∏ i = 1 tα i \\bar{\\alpha}_t = \\prod_{i=1}^t \\alpha_i αˉt​=∏i=1t​αi​
• σ t \\sigma_t σt​: 随机噪声缩放因子
• $ϵ$: 额外高斯噪声（仅随机性采样器添加）

不同采样器的差异体现在：

1. 噪声预测的利用方式（如一阶/二阶近似）；
2. 是否注入随机噪声 $ϵ$（决定收敛性）；
3. 历史步长的参考数量（如单步/多步优化）。

🔬 二、主流采样方法分类与公式解析

📊 1. 基础确定性采样器（收敛型，没有随机噪声）

采样器 公式特点 优势 局限 Euler 一阶更新：仅用当前步噪声预测， z t − 1 = f ( z t , ϵ θ ) z_{t-1} = f(z_t, \\epsilon_\\theta) zt−1​=f(zt​,ϵθ​) 速度最快，20-30步可收敛 细节精度较低，高步数易过拟合 Heun 二阶校正：需两次噪声预测， z t − 1 = z t − 1 α t ( 1 − α t ) ( 1 2 ϵ θ ( z t , t ) + 1 2 ϵ θ ( z t − 1 2 , t − 1 ) ) z_{t-1} = z_t - \\frac{1}{\\sqrt{\\alpha_t}} (1-\\alpha_t) \\left( \\frac{1}{2}\\epsilon_\\theta(z_t,t) + \\frac{1}{2}\\epsilon_\\theta(z_{t-\\frac{1}{2}},t-1) \\right) zt−1​=zt​−αt​ ​1​(1−αt​)(21​ϵθ​(zt​,t)+21​ϵθ​(zt−21​​,t−1)) 精度更高，减少伪影 速度慢2倍，显存消耗大 DDIM 非马尔可夫过程：支持跳跃更新， z t − 1 = α ˉ t − 1 ( z t − 1 − α ˉt ϵ θ α ˉ t ) + 1 −α ˉ t − 1 ϵ θ z_{t-1} = \\sqrt{\\bar{\\alpha}_{t-1}} \\left( \\frac{z_t - \\sqrt{1-\\bar{\\alpha}_t} \\epsilon_\\theta}{\\sqrt{\\bar{\\alpha}_t}} \\right) + \\sqrt{1-\\bar{\\alpha}_{t-1}} \\epsilon_\\theta zt−1​=αˉt−1​ ​(αˉt​ ​zt​−1−αˉt​ ​ϵθ​​)+1−αˉt−1​ ​ϵθ​ 10-15步生成可用图像，适合快速草图 高步数下细节不足

🎲 2. 随机性采样器（不收敛型）

采样器 公式特点 优势 局限 Euler a 添加随机噪声： z t − 1 = Euler公式 + σ t ϵ z_{t-1} = \\text{Euler公式} + \\sigma_t \\epsilon zt−1​=Euler公式+σt​ϵ 多样性高，适合创意生成 结果不可复现，可能扭曲细节 DPM++ SDE Karras 结合随机微分方程： z t − 1 = DPM++基础 + σ t ϵ z_{t-1} = \\text{DPM++基础} + \\sigma_t \\epsilon zt−1​=DPM++基础+σt​ϵ 细节丰富，写实质感强 需30-40步，速度慢

⚡ 3. 高效多步采样器（平衡型）

采样器 公式特点 优势 局限 DPM++ 2M Karras 二阶多步法：引入预测器-校正器，参考历史步长优化更新 速度-质量平衡最佳，20-30步即可高质量收敛 对动漫风格可能过度锐化 UniPC 统一预测校正器： z t − 1 = BH2变体 z_{t-1} = \\text{BH2变体} zt−1​=BH2变体，支持低阶最终采样 5-10步生成高质量图像，速度最快 高分辨率需选uniform skip type

⚠️ 4. 淘汰或不推荐采样器

• PLMS：早期替代DDIM，稳定性差，易产生色块；
• DPM fast：步数<20时可用，但质量不可控；
• DPM adaptive：无视用户步数设置，耗时长且结果不稳定。

📊 三、关键参数对采样效果的影响

1. 随机噪声注入（ σ t ϵ \\sigma_t \\epsilon σt​ϵ)：
   • 收敛性：若 σ t = 0 \\sigma_t = 0 σt​=0（如Euler、DPM++ 2M），结果可复现；若 σ t > 0 \\sigma_t > 0 σt​>0（如Euler a），结果随机。
2. 噪声调度器：
   • Karras调度：优化后期降噪梯度，减少高步数下的伪影（如DPM++ 2M Karras）。
3. 阶数（Order）：
   • 二阶（2M）：平衡速度与精度；三阶（3M）：细节更精细但需>30步+低CFG（≤7）。

💎 四、总结：选择建议与典型场景

需求场景 推荐采样器 步数 关键特性 通用高质量 DPM++ 2M Karras 20-30 收敛快、细节适中，综合最优 极致写实细节 DPM++ SDE Karras 30-40 不收敛、细节丰富，适合人像/皮肤纹理 效率优先（草图） UniPC / DDIM 5-15 极速生成，适合创意探索 多样性创意 Euler a 20-30 随机性强，适合角色设计/艺术创作 动画风格 LMS Karras 20-25 低饱和度、线条柔和，减少锐化瑕疵

操作技巧：

• 固定种子（Seed）时，收敛型采样器可复现结果，随机型需设 $\eta =0$ 抑制变化；
• 高分辨率（≥512×512）建议搭配 Karras 调度 或 UniPC uniform skip 避免细节异常[citation:8]。

采样器的本质是数值求解扩散逆过程的算法实现，通过调整更新策略平衡生成速度、质量与可控性，是连接扩散模型理论与工程落地的核心枢纽。

2.5 与 DALL·E 2 的结构对比

组件 Stable Diffusion DALL·E 2 扩散空间 潜空间（VAE 压缩） 像素空间（直接生成） 条件控制 文本嵌入注入 U-Net 交叉注意力 双重条件（文本嵌入+图像嵌入） 先验模块 无 扩散先验（生成图像嵌入 Z_i） 计算效率 高（潜空间维度低） 低（像素空间计算量大）

2.6 设计优势与局限

• 优势：
  • 效率高：潜空间去噪用的是64×64的像素，相比于512×512，减少 64 倍计算量，支持消费级 GPU 生成 512px 图像。
  • 扩展性强：模块化设计支持图生图（Img2Img）、图像修复（Inpainting）等任务。
• 局限：
  • 细节损失：VAE 压缩可能导致高频细节模糊。
  • 属性绑定问题：复杂提示中物体属性易错位（如“红球在蓝盒子上”可能颜色颠倒）。

2.7 关于 Stable Diffusion 本地部署

看这篇文章。

2.7 总结

Stable Diffusion 的核心创新在于 “潜空间扩散”，通过 VAE 压缩、CLIP 语义引导和 U-Net 条件去噪，实现了高效且可控的图像生成。其模块化架构为后续扩展（如 ControlNet）奠定了基础，成为开源社区最广泛应用的文生图模型之一。