第六届全球校园人工智能算法精英大赛-算法巅峰专项赛(系列文章)-- 验证程序
前言
全球校园人工智能算法精英大赛”是江苏省人工智能学会举办的面向全球具有正式学籍的全日制高等院校及以上在校学生举办的算法竞赛。其中的算法巅峰专项赛是新赛道,2024年是其第一届比赛。

这篇主要讲 最后一题出现的各类错误,以及推测的官方验证程序。
去年很多同学,最后一题遇到不少奇怪的错误,肯定留下了遗憾以及不解,这篇文章的价值之一,就是解释这个错误的原因。
系列文章
1. 第六届全球校园人工智能算法精英大赛-算法巅峰专项赛(系列文章)-- 开篇
如果该系列文章阅读量破万,将分享那届比赛的 Rank 1 满分代码。
测试集介绍
最后一题,其实对应10个case,每个case数据规模不同,其得分权重也不同。
以2024年的专项赛为准,得分如下
可以发现
- 每个case得分并不一样
- 总体而言,越往后的case得分越高
- 最后一题的权重总得分,远高于前五题总和
错误信息介绍
常规的错误信息
- 超时 Time Limit Exceeded
- 编译错误 Compilation Error
- 运行时错误 Runtime Error
还有这个赛题特定的错误信息
- 存在多次穿越的点
- 存在重复的点
- 点数和图形数不一致
后续的内容讲详细介绍这三个错误,以及走过的弯路。
走过的弯路
先来谈谈这2个错误
- 存在多次穿越的点
- 存在重复的点
从字面上来看, 这2个错误描述,有什么区别吗?我是只能感叹 中文的博大精深。
让我们聚焦
重复 重复 重复
测试的数据集,其物体之间有交集(即存在公共点),那要如何处理这种情况呢?
这里有两种猜想
- 是消除重复点(仅保留一个),最后点集数变小
- 是替换重复点,最后点集数大小不变。
欧拉回路
既然有重复,是否可以去除重复的点,即保留一个,这也是欧拉回路思路的猜测基石。
由欧拉回路的定义,如果一个连通的无向图中,最多只有2个节点的度为奇数,则一定存在一条欧拉图(一笔画)。
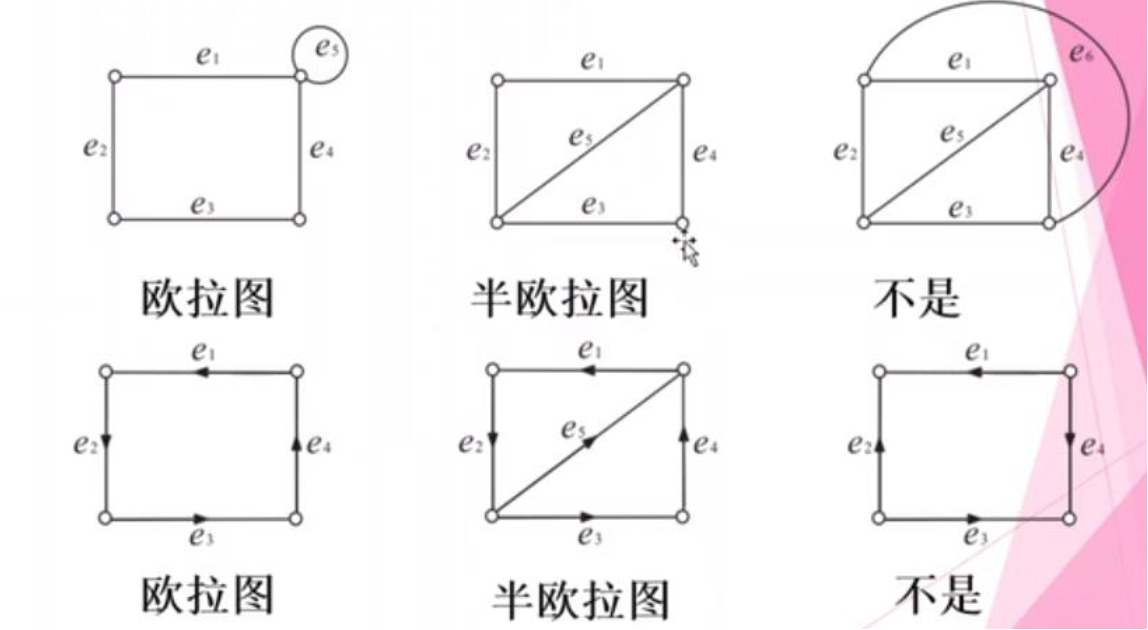
如果所有点都是偶数度,则必然能回到原点。

鉴于该定义,其实我们可以把有交集的物体(共点)合成为一个大物体。
核心:欧拉回路 + 并查集
但是这个思路,得到的错误反馈是
- 点数和图形数不一致
显然这个猜错是错的,真相只有第二种,即替换其他的重复点。
二分最大匹配
既然点数和图形数要一致,所以一种更合理的猜测和构造是。
点集 和 图形 的 配对数要最大,也就是二分完美匹配,转化一下就是求解
二分最大匹配问题 二分最大匹配问题 二分最大匹配问题
事实也是如此。
回到开头提到的2个错误:
- 存在多次穿越的点
- 存在重复的点
第一个问题其实是,点集和图形 不满足二分最大匹配。
第二个问题是,点集和图形,满足二分最大匹配,但是存在2个及以上相同的点。
还是用图,来解释下

比如这个路径,可以构建二分完美匹配,其中一个重复点属于上面方块,另一个重复点属于下面方块。把这种情况归纳为 存在重复点 ,但这个错误的前提是二分最大匹配。
这个重复,是该赛题 搞事情的 一个核心点,也是很多高手莫名翻车的原罪。
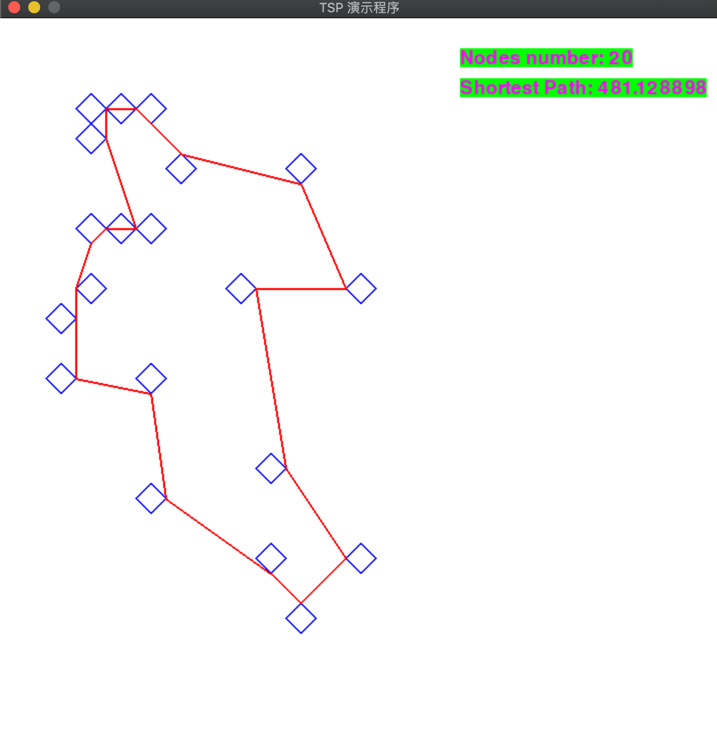
这个构造路径就是正确的,图形有共点,但是他满足二分最大匹配,同时无重复点。
推测的官方验证程序
结合以上的内容,我们编写一个验证程序
from collections import defaultdictclass Judger(object): @staticmethod def bpm(u, match, seen, g) -> bool: for v in g[u]: if not seen[v]: seen[v] = True if match[v] == -1 or Judger.bpm(match[v], match, seen, g): match[v] = u return True return False # 最大二分匹配, 匈牙利算法 @staticmethod def max_bipartite_matching(g) -> int: n = len(g) l = [i for i in range(n)] r = [i for i in range(n)] match = [-1] * len(r) result = 0 for u in l: seen = [False] * len(r) if Judger.bpm(u, match, seen, g): result += 1 return result # 构建二分图,并验证 @staticmethod def verify(path, d3d) -> bool: if len(path) != len(d3d): # 点数和图形数不匹配 return False hp = defaultdict(list[int]) for (i, ps) in enumerate(d3d): for (x, y) in ps: hp[(x, y)].append(i) g = [] for (i, p) in enumerate(path): if p not in hp: # 某个点不属于任何图形 return False g.append(hp[p]) if Judger.max_bipartite_matching(g) != len(d3d): # 存在多次穿越的点 return False if set(path) != len(d3d): # 存在重复的点 return False return True这个验证程序,应该高度接近官方实际的验证程序,非常自信。
写在最后
这篇文章,就相对比较枯燥了,如果没有写过2024年赛季的最后一题,是很难体会和共鸣。



