【B题成品论文】2025华数杯数学建模B题成品论文+可运行代码参考（无偿分享）

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

基于遗传算法与强化学习的无线资源管理优化模型研究

摘要

随着无线通信网络的快速发展，尤其是物联网和移动通信设备的普及，如何有效管理网络资源已成为亟待解决的关键问题。5G及未来网络采用异构蜂窝网络结构，包括宏基站和微基站的混合部署，如何在这一架构下优化资源分配、减少基站间干扰并提升网络效能，成为研究的核心挑战。本文针对这一问题，基于遗传算法（GA）、强化学习（RL）和粒子群优化（PSO）算法，提出了一种综合的无线资源管理优化模型，并在多个子问题上进行了求解。

针对问题一，本文通过遗传算法建立了资源分配模型，优化微基站的资源块分配，以最大化不同网络切片（URLLC、eMBB、mMTC）的服务质量。遗传算法模拟自然选择和遗传机制，能够有效地搜索解空间，处理复杂的组合优化问题。在资源分配过程中，采用了适应度函数来衡量每个切片的服务质量，通过精确调整每个切片的资源分配，确保总资源的最优利用。

针对问题二，本文采用强化学习（RL）方法解决了动态资源调整问题。由于用户的任务到达和信道质量是动态变化的，传统的优化方法难以应对此类多阶段决策问题。强化学习通过与环境的交互，自主学习最优的资源分配策略，能够实时适应变化的任务需求和信道状态，确保每次资源重新分配时，网络负载平衡并最大化用户的服务质量。Q-learning和深度Q网络（DQN）被用来处理复杂的状态空间，使得系统能够在动态环境中做出最优决策。

针对问题三，考虑到多个基站间的干扰影响，本文进一步引入了功率控制与干扰管理的优化模型。在多个基站共享频谱资源的情况下，基站之间的干扰会显著影响网络的性能，因此需要对基站的发射功率进行调节。遗传算法被用来优化基站的发射功率，通过控制每个基站的功率，不仅能够减少干扰，还能提升用户的服务质量，确保系统的整体效能。

针对问题四，本文专门应用遗传算法来解决用户接入决策与基站协同优化的问题。在宏基站和多个微基站的异构网络环境中，用户的接入决策直接影响其服务质量。通过遗传算法对每个用户的接入模式进行优化决策，并结合资源分配方案和功率控制策略，进一步提升了系统的服务质量。

针对问题五，本文引入了粒子群优化（PSO）算法来解决基站的能效优化问题。在保证用户服务质量的前提下，如何降低基站的能耗成为一项重要目标。PSO算法能够高效地在大规模的解空间中搜索最优的能效和服务质量之间的平衡，通过优化资源调度和功率控制策略，实现了多目标优化。

最后，我们对提出的模型进行了全面评价：该模型有效结合实际需求，能合理解决多基站资源分配、功率控制和干扰管理等问题，具备较强的实用性和算法效率，且在未来网络中具有广泛的应用前景。

关键词： 遗传算法  强化学习  粒子群优化  资源管理优化  多目标优化

• 问题重述
  1. 问题背景

随着物联网和移动通信设备的快速增长，数据需求呈现爆发式增加，推动了无线通信网络架构的演进。为了应对不同的场景需求，5G及未来的网络逐步采用了异构蜂窝网络结构，包括宏基站和微基站的混合部署，宏基站提供大范围覆盖，微基站则在高密度区域提供高效的无线接入。这种网络架构能够显著提升容量和用户体验，尤其是在超高设备接入和大数据传输的情况下，如何有效分配资源、避免干扰、提升服务质量，成为了研究的关键问题。

5G网络通过网络切片技术将物理网络划分为多个虚拟化的逻辑切片，满足不同应用需求，如高可靠低时延的URLLC、增强移动宽带的eMBB和大规模机器通信的mMTC切片。切片之间共享频谱资源，这就要求对每个切片的资源分配进行动态优化，以提高频谱利用率并保证不同切片间的干扰最小化。在此背景下，本题目旨在设计一种无线资源管理方案，确保不同切片的资源分配既能够最大化系统整体的服务质量，又能控制基站的干扰，提升网络的整体效能和能效。

1. 1. 问题提出

问题一：资源分配优化：一个微基站拥有50个资源块，需要将其分配给三种网络切片（URLLC、eMBB、mMTC）。要求根据每个切片的服务需求，将这些资源块合理分配，以最大化用户的服务质量。

问题二：动态资源调整：考虑到用户可能会频繁发起传输请求并且发生移动，导致信道的动态变化，系统需要在每100ms重新调整资源分配。目标是在考虑未来任务到达及排队队列的情况下，动态优化每次决策的资源分配方案，以确保用户的服务质量最大化。

问题三：干扰控制与功率优化：在多个微基站共同工作时，基站间会产生干扰。为了优化频谱利用率和降低干扰，每个基站不仅要进行资源分配，还需要控制发射功率。目标是通过合理的功率控制，最小化系统干扰，同时最大化用户的服务质量。

问题四：用户接入决策与基站协同：在一个宏基站和多个微基站共同工作的异构网络中，用户需要决定是接入最近的微基站还是宏基站。系统需要通过优化用户接入决策及基站的资源分配方案，以最大化整体用户的服务质量。

问题五：能效优化：在保障服务质量的前提下，如何减少基站的能耗成为一个重要目标。需要通过合理的资源调度与功率控制，在降低能耗的同时，确保用户服务质量的最大化，以实现绿色通信网络。

• 问题分析

问题一：在该问题中，微基站需要在有限的50个资源块中进行资源分配，涉及的切片类型包括URLLC、eMBB和mMTC。每个切片对服务质量有不同的需求，目标是根据每类切片的优先级和传输需求，合理地分配资源块，从而最大化整体服务质量。这需要在保证总资源使用限制的前提下，精确调整每个切片的资源分配。

问题二：在多次传输请求和用户移动的动态环境中，系统需要根据每个时刻的任务到达情况和信道变化，实时调整资源分配。此问题要求对系统进行多次决策，以适应用户需求和信道条件的波动，确保在每次资源重新分配时，能够平衡网络负载并最大化用户的服务质量。

问题三：当多个基站共享频谱资源时，基站之间的干扰会影响通信质量。此问题要求在资源分配的同时，考虑如何调整每个基站的发射功率，减少干扰并提升用户体验。基站的发射功率控制方案需要与资源分配策略相结合，以确保在减少干扰的同时最大化系统的整体性能。

问题四：在宏基站和多个微基站的混合网络环境中，用户的接入决策将直接影响其服务质量。此问题要求对每个用户的接入模式进行优化决策，确定用户是接入宏基站还是微基站，同时合理分配资源和调整功率，以保证系统的整体服务质量。

问题五：随着网络的扩展和运营成本的增加，基站的能效优化变得尤为重要。此问题需要在保证用户服务质量的前提下，通过优化资源分配和功率控制策略，降低基站的能耗。通过平衡服务质量和能效，系统可以实现低成本、高效能的运作，满足绿色通信的要求。

• 模型假设与符号说明
  1. 模型基本假设

1. 资源块分配为离散整数：每个资源块的分配为离散的整数值，且每个基站分配的资源总数不能超过其可用资源。
2. 任务服务质量要求固定：每个切片对服务质量的要求（如速率、延迟等）是固定的，不随时间变化。
3. 用户接入模式优先级：在网络资源不足的情况下，优先为URLLC切片分配资源，以确保延迟要求得到满足。

优化过程中的功率损耗系数恒定：基站的功率损耗系数在优化过程中被假设为常数，不随功率调节变化。

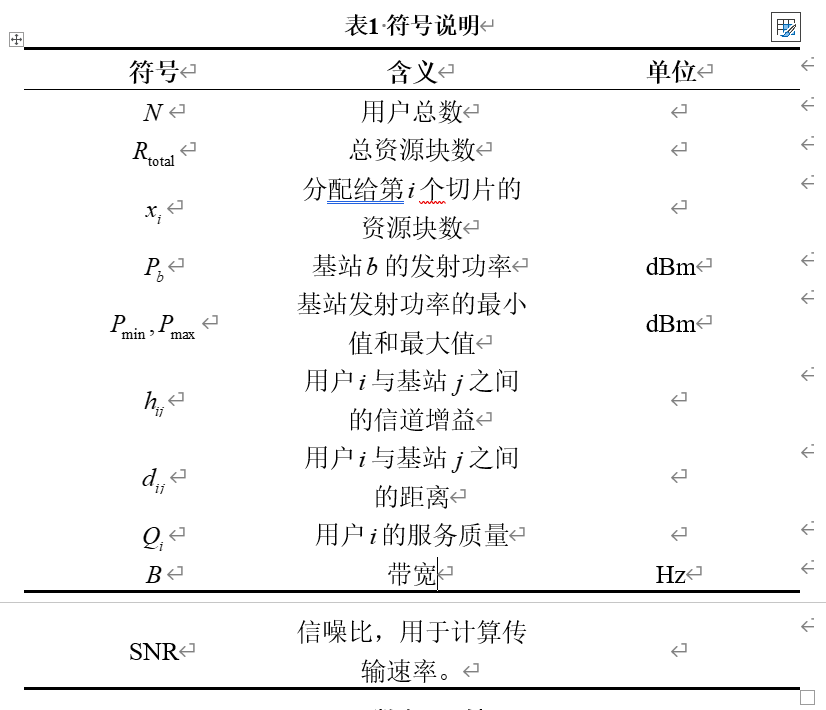
3.2符号说明

四、 数据预处理

4.1 数据清洗

数据处理是数学建模过程中的关键环节，它决定了模型的准确性和求解效率。本研究对数据进行了清洗、归一化、特征选择等步骤，以确保数据的质量，并为后续模型提供可靠的输入。

数据清洗:

数据清洗的主要目的是剔除缺失值和异常值，确保输入数据的质量。原始数据中部分用户的任务存在缺失值或异常值。为了处理这些问题，我们采用了以下方法：

对缺失值进行均值填充或插值法处理，确保数据的连续性。

对异常值进行剔除，通过箱线图识别并去除超出合理范围的异常数据。

数据归一化:

为了避免特征之间的尺度差异对模型训练造成影响，我们对数据进行了归一化处理。归一化采用的公式如下：

其中，为原始数据，和分别为该特征的最小值和最大值，x\'为归一化后的值，范围为[0, 1]。通过归一化，确保各个特征在相同的尺度下进行比较，有助于提升模型的训练效果。

在数据处理过程中，主要目标是确保输入数据的质量和准确性，同时对特征进行合理选择和预处理，使得后续的模型优化能够更高效地运行。

五、 模型建立与求解

1.1 问题一模型建立与求解

1.1.1 问题一求解思路

本问题要求在一个微基站的50个资源块中，优化分配给三种不同的网络切片（URLLC、eMBB、mMTC）。通过遗传算法，我们可以根据每个切片对服务质量的需求，合理分配资源块，以最大化用户的服务质量。URLLC切片需重点关注时延，eMBB则关注传输速率，而mMTC侧重于连接性。目标是通过精确调整资源分配，使得三类切片的服务质量达到最优。

1.1.2 问题一模型建立

1 建模过程

1.1 资源块分配与服务质量

首先，微基站拥有50个资源块，需要根据每类切片的需求和服务质量要求进行分配。具体来说，URLLC、eMBB和mMTC切片在资源块分配时具有不同的服务质量要求。

每个切片的服务质量与其分配到的资源块数量密切相关。通过以下公式来定义不同切片的服务质量：

（1）URLLC 切片：

URLCC 切片对时延有严格要求，因此其服务质量函数以延迟为主要考量因素。设任务的总延迟为 ，其中 为排队延迟，为传输延迟。若总延迟 超过了最大容忍时延，则任务丢失，其服务质量降为0。否则，服务质量为：

其中， 是折扣系数，为该类切片的时延要求。

（2）eMBB 切片：

eMBB 切片的服务质量由任务的传输速率决定。如果速率 r 达到 ，且延迟 d\\le SL{{A}_{\\text{eMBB}}}，服务质量为：

其中，r 为传输速率，为该类切片的速率要求，为速率未达到要求时的惩罚系数。

（3）mMTC 切片：

mMTC 切片侧重于连接性，服务质量由任务接入比例 决定。若任务成功接入，则，否则 ，总服务质量可以表示为：

其中，为该类切片的最大接入比例， 为任务丢失的惩罚系数。

1.2 资源分配约束

由于微基站共有50个资源块，因此资源分配必须满足以下约束条件：

其中，、、分别表示分配给URLLC、eMBB和mMTC切片的资源块数。

1.3 目标函数

我们的目标是最大化总服务质量。总服务质量是三类切片服务质量的加权和，具体为：

其中，，，为每个切片的权重系数，表示不同切片对总服务质量的贡献。

2. 优化方法：遗传算法（GA）

为了找到最优的资源块分配方案，采用遗传算法（GA）来进行优化。遗传算法是一种模拟自然选择和遗传机制的搜索算法，适合于解决组合优化问题。遗传算法的步骤如下：

2.1 初始化种群

生成一组初始解，每个解表示一种资源块分配方案。每个个体由三个变量组成，分别为分配给URLLC、eMBB和mMTC切片的资源块数量， 和 ，并满足约束条件：

2.2 适应度函数

计算每个解的适应度，即该资源块分配方案对应的总服务质量 ，作为适应度函数：

2.3 选择操作

根据适应度选择父代个体。适应度较高的个体更有可能被选中进入交叉和变异操作。常用的选择方法有轮盘赌选择和锦标赛选择。

2.4 交叉操作

通过交叉操作，选择两个父代个体，并交换它们的一部分基因，生成两个子代个体。交叉操作有助于搜索空间的扩展和解的多样性。

2.5 变异操作

变异操作通过随机改变部分个体的资源块分配量，以增加解空间的多样性，避免陷入局部最优解。

2.6 更新种群

将交叉和变异后的子代个体与父代个体结合，并选择适应度较高的个体组成下一代种群。

2.7 终止条件

当达到预设的代数或适应度收敛时，停止算法并返回最优解。

后续都在“数模加油站”......