网站导航
> 技术文档 > 数学建模——模拟退火算法（SA）_模拟退火 数学建模

数学建模——模拟退火算法（SA）_模拟退火 数学建模

网友: 技术文档 2025-09-03 22:19:14

1.概念

模拟退火算法（Simulated Annealing, SA）是一种基于蒙特卡洛思想的全局优化算法，灵感来源于固体退火过程。该算法通过模拟高温物体逐渐冷却的过程，在解空间中随机搜索最优解，具有跳出局部最优的能力。

模拟退火的核心思想源于热力学中的退火过程：高温下粒子能量高，状态随机性强；随着温度降低，系统逐渐趋于稳定。

举个例子，比如你要从高空往山底飞，一开始高空全是雾，你不知道最低点在哪里，你可以到处飞，随着高度下降，你所看到的区域最低点越来越清楚，而其他地方的最低点越来越难看到，最后你能完全看到你所在区域的最低点，从而找到一个相对理想的最低点

&&模拟退火相较于蒙特卡罗法就在于模拟退火不是完全随机

比如现在把一个登山者随机放在山里面的任何一个位置，要求登山者找到最高峰，蒙特卡罗法是生成大量的位置，找所有位置里面的最高点。而模拟退火是有规则的，下一个位置要是比一开始的位置低那只能有概率接受，而概率也和退火时间（温度）相关

&&模拟退火相较于爬山法就在于模拟退火不是完全遵循规则

爬山法中爬山的人只能向上爬，爬到局部最优时周围的点当然更低，全都不接受，然后就会卡在局部最优

爬山法 模拟退火法 蒙特卡罗法 区别 只能向上爬，爬到局部最优 下一个位置要是比一开始的位置低那只能有概率接受 生成大量的位置，找所有位置里面的最高点 随机or规则 完全遵循规则 规则+随机 完全随机 缺点 会陷入局部最优 在规则下随机，可以跳出局部最优也减少运气影响 运气成分太大，模拟次数要求多

2.算法流程

模拟退火有两层循环

其中外层循环主要是用来降温，内层循环用来选择解

1.伪代码如下：

# 初始化x ← x₀  # 当前解best ← x # 历史最优T ← T₀k ← 0while T > T_min and k < max_iter: for i = 1 .. L_k: # 每个温度的内部循环 y ← Neighbor(x)  # 产生邻域解 ΔE ← E(y) - E(x) if ΔE < 0:  # 更好解 → 直接接受 x ← y if E(y) < E(best): best ← y else: # 更差解 → 按概率接受 if rand() < exp(-ΔE / T): x ← y T ← α * T # 降温 k ← k + 1 (可选) L_k ← UpdateLength(T) # 动态调整链长return best

2.流程图

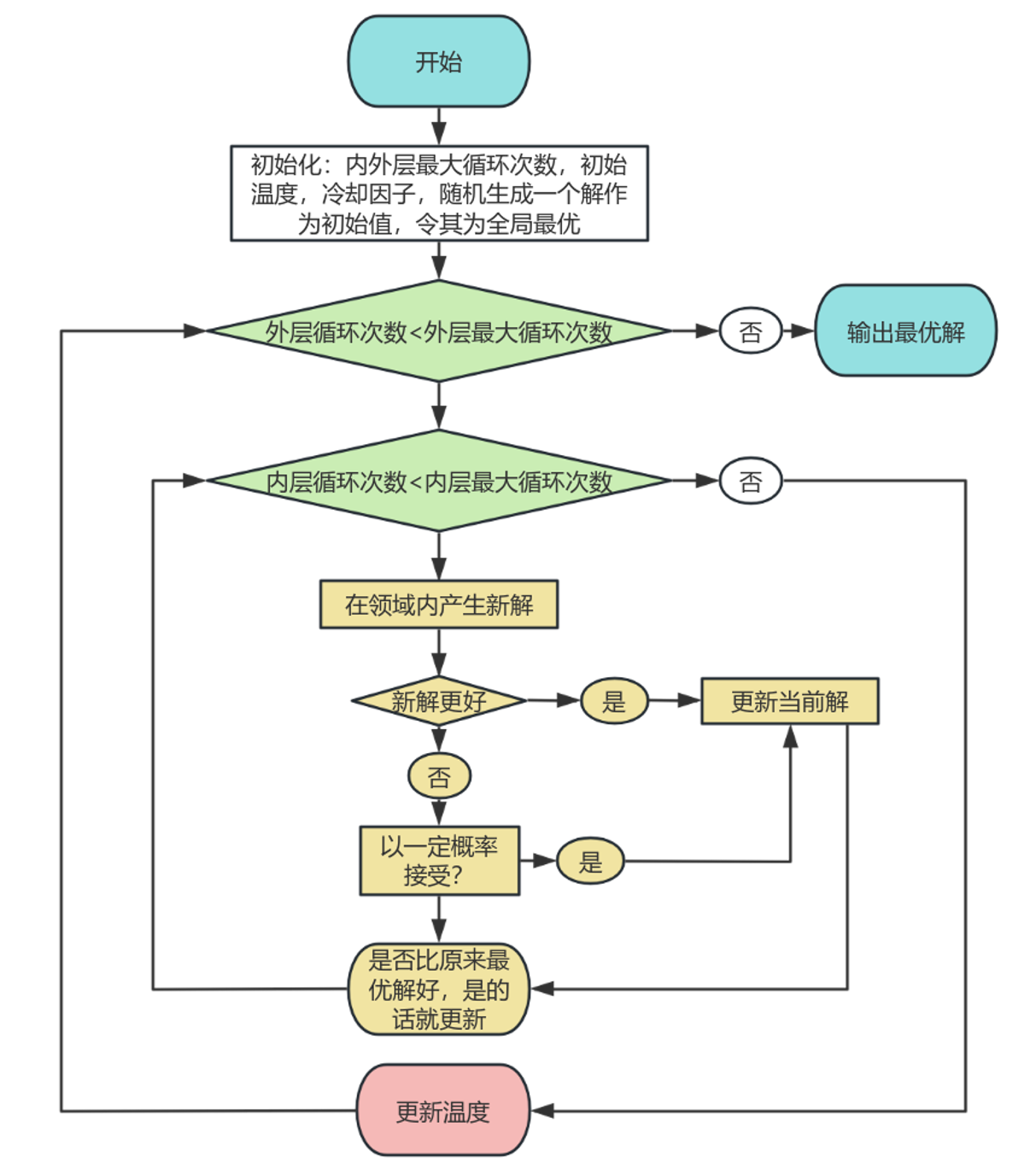
3.细节 

当然这里面有细节没说清楚

1.以一定概率接受，一定概率是多少？

这就是著名的 Metropolis 接受概率：

其中T=T_0*\\alpha^t

T0 \\alpha t 是初始温度一般是100 是降温系数一般是0.95 是降温时间，这里一般是外层循环次数

 这个函数其实是一个单调递减的函数，接受概率与成负相关，也就是说接受概率与差值是负相关，与温度是正相关

当差值越大时，接受概率就会比较低，意思是新旧值之间离的近才容易接受

对于温度，退火的过程中温度是逐渐降低的，而温度越低接受度越低，也就是说越到后面越不接受不理想值而一开始T是100，让几乎为0，接受度几乎是100％，意思就是一开始允许乱选点，即使是不好的点也允许选，为什么？因为这样可以保证选的范围尽可能大，这样容易找到最优解所在的区间

2.模拟退火中要在附近找一个新解，附近怎么定义，新解怎么算

“附近”就是邻域（neighborhood）的定义，它是模拟退火算法里问题相关、算法无关的部分。
只要满足一条：从当前解 x 出发，用若干“简单变换”能一步到达的全体解的集合 N(x)。
如何“算”新解，完全取决于你用什么变换规则。

旅行商问题（TSP） 任选两城市 i<j，把 i…j 之间的路径反转 把i，j城市交换位置 01背包问题 随机把一个物品 0↔1

函数优化

方法1：

delta = (UpperBound - LowerBound); % 变量范围sigma = T .* delta; % 温度越高，sigma 越大x_new = x + sigma .* randn(size(x)); % 高斯扰动x_new = max(min(x_new, UpperBound), LowerBound); % 裁剪到边界

方法2： 

y=randn(1,narvs);%生成一行narvs列的N(0,1)随机数 z=y/sqrt(sum(y.^2)); x_new=x0+z*T; for j=1:narvs if x_new(j)x_max(j) r=rand(1); x_new(j)=r*x_max(j)+(1-r)*x0(j); end end
小细节 
1.如果你看的仔细，可能会发现这个x_new很容易越界

下面给两种方式处理

1.强行截断取上下界

x_new = max(min(x_new, UpperBound), LowerBound); % 裁剪到边界

这个方法很容易出现温度较高时在最大最小值之间跳动，导致计算多余

解决方法是找到合适的初始温度，如果温度较低就提高降温系数 

2.找一个初始的x，假如新x越下界，就在下界和x中随机选一个数，越过上界同理

 for j=1:narvs if x_new(j)x_max(j) r=rand(1); x_new(j)=r*x_max(j)+(1-r)*x0(j); end end
2.模拟退火的核心

为什么早期“大步”也算邻域？

模拟退火里的 neighborhood 定义 并不是“几何距离很小的点”，而是

“在当前温度下，算法愿意尝试的点”。

早期高温时，系统允许大幅度跳跃，因为接受度很大，因此 整个定义域 都被视为潜在邻域，这样保证不会陷入局部最优；随着温度降低，邻域概念才真正缩回到“局部”，因为接受度越来越小。

3.疑惑

1.为什么模拟退火算法最后一定会是一个相对最优解

模拟退火算法（Simulated Annealing, SA）最终不保证找到全局最优解，但它大概率会收敛到一个“相对最优解”（即接近全局最优的局部最优）。其核心逻辑依赖于概率性接受劣解和退火温度的衰减，具体原因如下：

1. 概率性跳出局部最优

  • Metropolis准则：算法以一定概率 e−ΔE/T 接受劣解（ΔE>0），其中 T 是温度。在高温阶段，接受概率高，允许探索更差的解；随着 T 降低，接受概率趋近于0，逐渐收敛到局部区域。

  • 关键作用：这种机制使算法在早期阶段能跳出浅层局部最优，后期则稳定在当前区域，避免无休止的随机游走。

2. 温度衰减的平衡

  • 退火计划：温度按 Tk+1​=αTk​（0<α<1）衰减，若衰减足够慢（如 α≈0.99），算法会经历“充分探索→局部精炼”的过程。

  • 理论保证：若采用对数衰减 Tk​=ln(k+1)C​，理论上可收敛到全局最优（但计算成本极高，实际中不可行）。实际应用中，指数衰减更常见，此时只能保证“相对最优”。

类比解释

想象一个凹凸不平的球面：

  • 高温阶段：球（当前解）被剧烈摇晃，可能翻越任何障碍（跳出局部最优）。

  • 低温阶段：摇晃减弱，球最终停在一个较深的谷底（局部最优），但不一定是全局最深的谷底。

2.有没有可能收敛到另一个局部最优 

最后不一定是整体最优，甚至连“相对最优”都不保证——它只是一个随机过程，最终停在哪个局部最优完全取决于：

  1. 退火速度（降温调度）
    降温太快，系统可能“过早冻结”在某个局部最优，连附近更好的解都没机会探索。

  2. 随机路径（蒙特卡洛抽样）
    即使退火速度合适，如果随机抽样“运气不好”，始终没碰到通往全局最优的路径，也会卡在另一个局部最优。

  3. 问题本身的能量景观
    如果全局最优被“高能量壁垒”包围，而算法没在高温阶段跨越过去，最终就进不去那个“盆地”。

3.那为什么还要选择模拟退火算法 

因为它在“够快”和“够好”之间，提供了一个工程上最划算的折中方案。

下面分场景给出更具体的理由：

  1. 问题本身太“丑”

    • 非凸、非光滑、维度高、组合爆炸（如 TSP、VLSI 布局、超参调优）。

    • 传统梯度法/整数规划/动态规划要么根本用不了，要么算到天荒地老。
      ➔ SA 只需一个“能量函数”即可开跑，写 20 行代码就能得到一个“还不错的可行解”。

  2. 要求“随时可用、随时可停”

    • 实际项目经常有时间/预算上限（例如 10 分钟、1000 次能量评估）。

    • SA 天然支持“任何时刻中断并取当前最佳解”，而很多精确算法必须跑完才有结果。

  3. 实现成本极低，通用性强

    • 与问题领域无关：只要你能定义“解”和“能量/代价”，就能套模板。

    • 对比遗传算法、粒子群、蚁群等，SA 参数少（主要是温度调度），调试门槛低。

4.为什么降低温度足够慢也会收敛到全局最优，选点不是随机的吗 

 最高点左右往上爬的机会更多，比如我在最高点附近，我选择附近的点，还是能继续往上爬的，这个是容易接受的，而不是最高点，就算能往上爬一段，也会在中途找不到更高的点，即使能接受一部分低点作为新x，但是总有跳走的时候

 4.运行结果

完整20000次

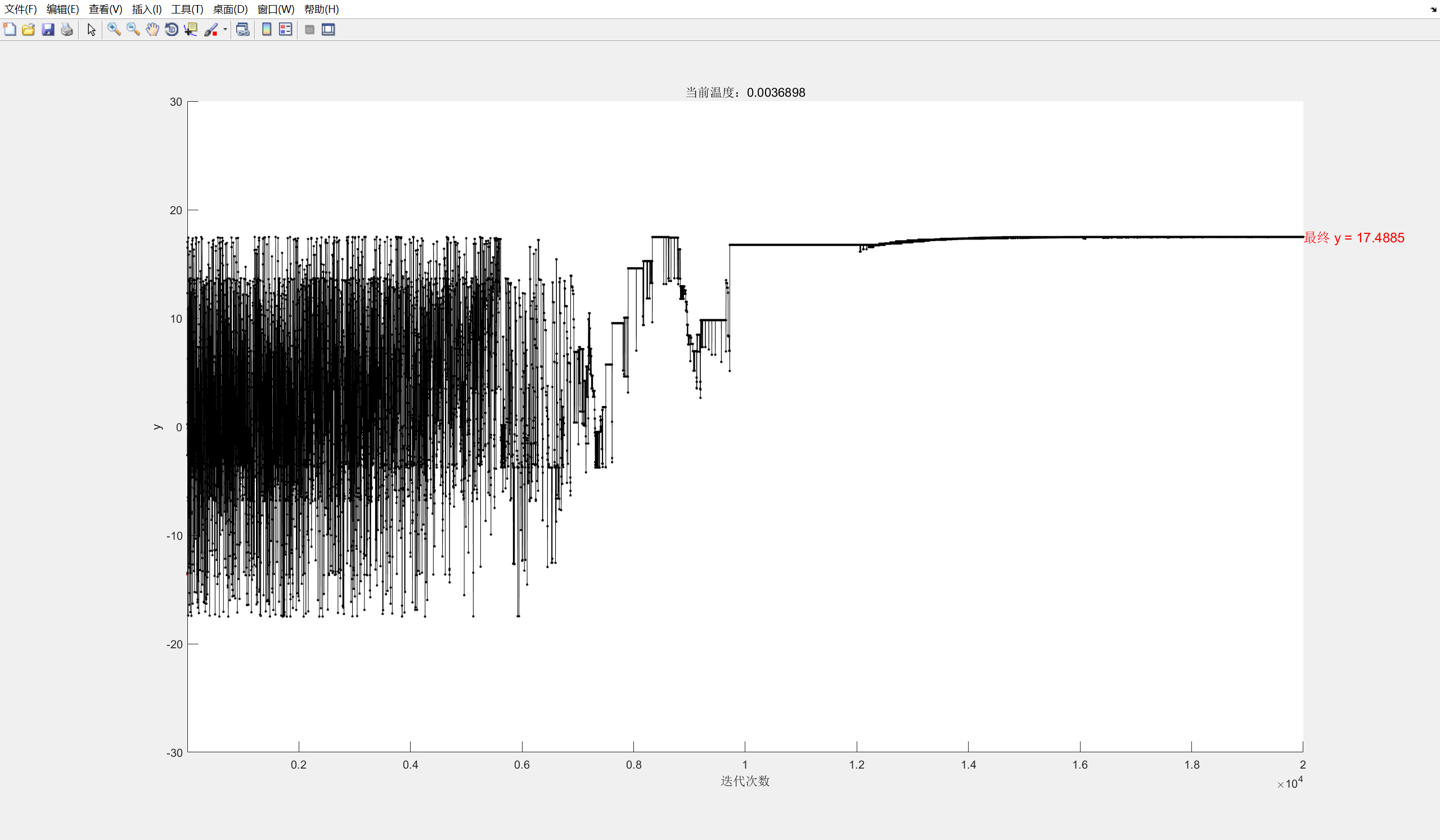
只看外层200次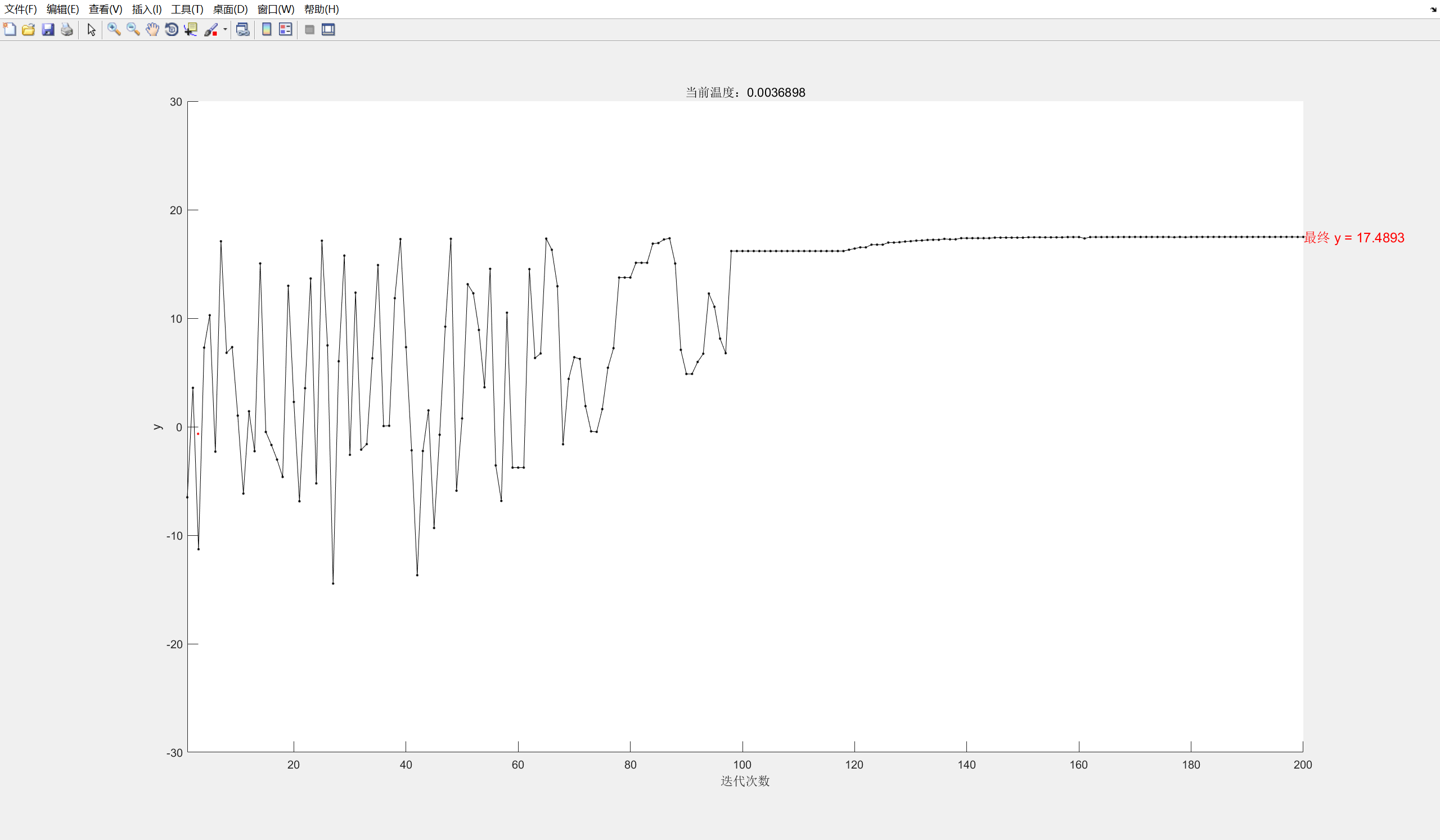

从这个图我们可以看到，有的时候都找到最大值了，但是由于运气问题会跳到非最大值，不过由于次数足够大，最终还是会找到一个比较好的结果 

网络标签：

相关问题