动态规划（背包问题）_背包问题 动态规划

一.背包问题

（1）01背包

问题核心：在有限容量的背包中，如何选择物品以获得最大价值” 的问题，其中每个物品只能选择一次（要么放入，要么不放入）

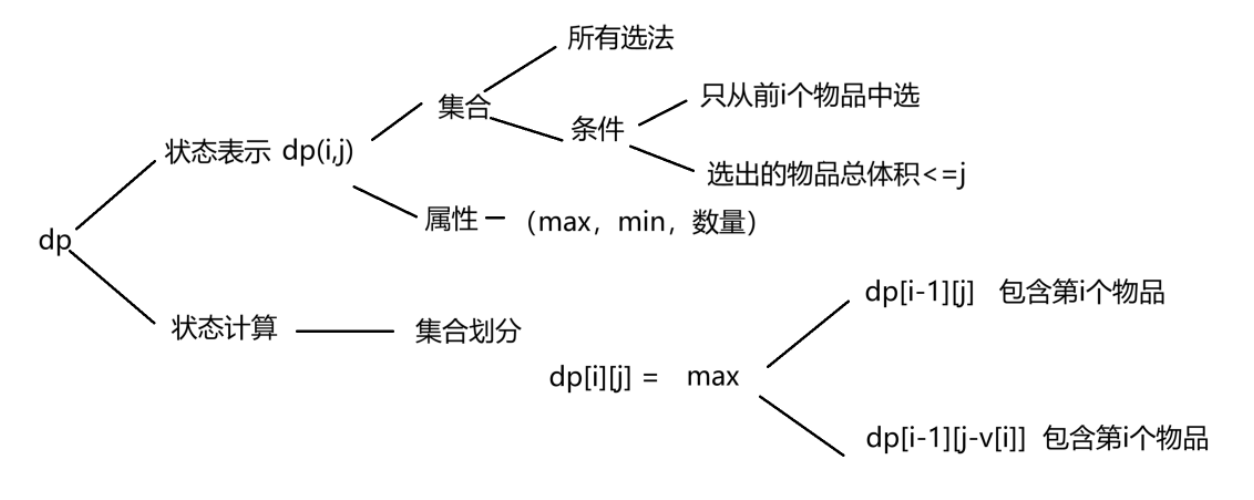
通过构建一个 DP 数组，记录 “在特定容量下能获得的最大价值”，逐步推导最优解。

设 dp[i][c] 表示 前 i 个物品（0 到 i-1）在背包容量为 c 时的最大价值。

对于第 i 个物品（索引 i-1），有两种选择：

不放入：最大价值等于前 i-1 个物品在容量 c 时的价值，即 dp[i][c] = dp[i-1][c]；

放入（满足 v[i-1] ≤ c）：价值为 “前 i-1 个物品在容量 c - [i-1] 时的价值” 加上当前物品的价值，即 dp[i][c] = dp[i-1][c - v[i-1]] + w[i-1]。

因此，状态转移方程为：
dp[i][c] = max(dp[i-1][c], dp[i-1][c - v[i-1]] + w[i-1])（若 v[i-1] ≤ c，否则取前者）。

题目描述

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi​，价值是 wi​。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
接下来有 N 行，每行两个整数 vi​、wi​，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤10000<vi​,wi​≤1000

输入样例

4 51 22 43 44 5

输出样例

8

代码实现

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =1e3+10;int n,m;int v[N],w[N];int dp[N][N];int main() { cin>>n>>m; for(int i = 1;i>v[i]>>w[i]; for(int i = 1;i<=n;i++)//枚举所有物品 { for(int j = 0;j=v[i]) dp[i][j] = max(dp[i][j],dp[i-1][j-v[i]]+w[i]); } } cout<<dp[n][m]; return 0;} 

优化成一维数组：

此时，为了保证每个物品只被选择一次，体积要从大到小枚举。

一维数组dp[j]的更新依赖于上一轮（处理前 i-1 个物品时）的状态，而非当前轮（处理第 i 个物品时）的状态。

假设从小到大遍历容量j（从v[i]到m）：

当计算dp[j]时，dp[j - v[i]]可能已经被更新过（因为j - v[i] < j，更早被遍历）。

这意味着dp[j - v[i]]已经包含了第 i 个物品的价值，此时再加上w[i]就相当于重复选择了第 i 个物品，违背了 01 背包的规则（变成了 “完全背包” 的逻辑）。

当从大到小遍历容量j（从m到v[i]）：

计算dp[j]时，j - v[i] < j，而j - v[i]尚未被遍历（因为我们从大到小处理），所以dp[j - v[i]]仍然是上一轮（前 i-1 个物品）的状态。

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =1e3+10;int n,m;int v[N],w[N];int dp[N];int main() { cin>>n>>m; for(int i = 1;i>v[i]>>w[i]; for(int i = 1;i=v[i];j--)//枚举所有体积 { dp[j] = max(dp[j],dp[j-v[i]]+w[i]); } } cout<<dp[m]; return 0;} 

（2）完全背包

问题核心：物品可以被无限次选取（只要背包容量允许）。

设 dp[i][c] 表示 前 i 个物品（0 到 i-1）在背包容量为 c 时的最大价值。

对于第 i 个物品（索引 i-1），因可重复选，选择逻辑变为：

不放入：同 01 背包，dp[i][c] = dp[i-1][c]；

放入（需满足 k*v[i-1] ≤ c）：若放入第 i 个物品，由于还能继续选它，因此状态应基于当前物品已选至少一次的情况，即 dp[i][c] = dp[i][c - k*v[i-1]] + k*w[i-1](k>=0)

完全背包问题

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。
第 i 种物品的体积是 vi​，价值是 wi​。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行两个整数 vi​、wi​，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤10000<vi​,wi​≤1000

输入样例

4 51 22 43 44 5

输出样例

10

代码实现

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =1e3+10;int n,m;int v[N],w[N];int dp[N][N];int main() { cin >> n >> m; // 输入物品种类数和背包容量 // 输入每种物品的体积和价值 for(int i = 1; i > v[i] >> w[i]; } // 动态规划求解 for(int i = 1; i <= n; i++) { // 枚举每种物品 for(int j = 1; j <= m; j++) { // 枚举所有可能的容量 // 不选第i种物品时的最大价值 dp[i][j] = dp[i-1][j]; // 枚举第i种物品的选择数量k（k≥1） for(int k = 1; k * v[i] <= j; k++) { // 状态转移：选择k个第i种物品时的最大价值 dp[i][j] = max(dp[i][j], dp[i-1][j - k*v[i]] + k*w[i]); } } } cout << dp[n][m]; // 输出容量为m时的最大价值 return 0;} 

优化成一维数组

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =1e3+10;int n,m;int v[N],w[N];int dp[N];int main() { cin >> n >> m; // 输入物品种类数和背包容量 // 输入每种物品的体积和价值 for(int i = 1; i > v[i] >> w[i]; } // 动态规划求解 for(int i = 1; i <= n; i++) { // 枚举每种物品 for(int j = v[i]; j <= m; j++) //因为一个物品可以重复选择，那么就不用从大到小枚举 { dp[j] = max(dp[j],dp[j-v[i]]+w[i]); } } cout << dp[m]; // 输出容量为m时的最大价值 return 0;} 

（3）多重背包问题

问题核心：每种物品有固定的数量限制（既不能像 01 背包那样只能选 1 次，也不能像完全背包那样无限选）

对于第 i 种物品，可选择的数量 k 满足：0 ≤ k ≤ s[i] 且 k × v[i] ≤ c（总重量不超过容量）。
因此，状态转移方程为：
dp[i][c] = max{ dp[i-1][c - k × v[i]] + k × w[i] }（其中 k 取 0 到最大可能值）。

当 k=0 时：不选第 i 种物品，价值为 dp[i-1][c]；

当 k>0 时：选 k 个第 i 种物品，价值为 “前 i-1 种物品在剩余容量 c - k×v[i] 时的价值” 加上 k 个物品的总价值。

题目描述

有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si​ 件，每件体积是 vi​，价值是 wi​。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行三个整数 vi​、wi​、si​，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000<vi​,wi​,si​≤100

输入样例

4 5 1 2 3 2 4 1 3 4 3 4 5 2 

输出样例
 

10

代码实现

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =1e3+10;int n,m;int v[N],w[N],s[N];// v[i]：体积；w[i]：价值；s[i]：该物品的最大数量int dp[N][N];int main() { cin >> n >> m; // 输入物品种类数和背包容量 // 输入每种物品的体积和价值 for(int i = 1; i > v[i] >> w[i]>>s[i]; } // 动态规划求解 for(int i = 1; i <= n; i++) { // 枚举每种物品 for(int j = 0;j<=m;j++) { for(int k = 0;k*v[i]<=j&&k<=s[i];k++)// 枚举第i种物品的选择数量k（0到最大可能数量） { dp[i][j] = max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]); } } } cout << dp[n][m]; // 输出容量为m时的最大价值 return 0;} 

 多重背包优化

多重背包的二进制优化原理核心是通过将物品数量拆分为 2 的幂次方组合，且这些数的组合能表示 0~s 之间的所有整数

将每个原物品拆分为 log2(s)+1 个虚拟物品后：

每个虚拟物品的体积 = 原体积 × 拆分的数量（如 k=2 时，虚拟体积 = v×2）

每个虚拟物品的价值 = 原价值 × 拆分的数量（如 k=2 时，虚拟价值 = w×2）

此时，多重背包问题转化为 01 背包问题—— 每个虚拟物品只能选择一次，但其组合可覆盖原物品所有可能的选取数量（0 到s）

题目描述

第 i 种物品最多有 si​ 件，每件体积是 vi​，价值是 wi​。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。
接下来有 N 行，每行三个整数 vi​、wi​、si​，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N≤10000<V≤20000<vi​,wi​,si​≤2000

输入样例

4 5 1 2 3 2 4 1 3 4 3 4 5 2 

输出样例

10

代码实现 

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =25000;int n,m;int v[N],w[N],s[N];int dp[N];int main() { int n,m;cin>>n>>m; int cnt = 0; // 记录拆分后虚拟物品的总数 for(int i = 1; i > a >> b >> s; int k = 1; // 二进制拆分的基数（1, 2, 4, 8...） while(k 0） if(s > 0) { cnt++; v[cnt] = a * s; w[cnt] = b * s; } } // 对拆分后的虚拟物品应用01背包解法 for(int i = 1; i = v[i]; j--) { dp[j] = max(dp[j], dp[j - v[i]] + w[i]); } } cout<<dp[m]; return 0;} 

（3）分组背包问题 

问题核心：物品被划分为若干组，每组中最多选一个物品 。

选该组的第 j 个物品（需满足 v[k][j] ≤ c）：价值为 “前 k-1 组在容量 c - v[k][j] 时的价值” 加上当前物品的价值，即 dp[k][c] = max(dp[k][c], dp[k-1][c - v[k][j]] + w[k][j])。

题目描述

有 N 组物品和一个容量是 V 的背包。
每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vi,j​，价值是 wi,j​，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式

第一行有两个整数，N，V，用空格隔开，分别表示物品组数和背包容积。

接下来有 N 组数据：

每组数据第一行有一个整数 Si​，表示第 i 个物品组的物品数量；

每组数据接下来有 Si​ 行，每行有两个整数 vi,j​、wi,j​，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000<Si​≤1000<vi,j​,wi,j​≤100

输入样例

3 5 2 1 2 2 4 1 3 4 1 4 5 

输出样例

8 

代码实现 

#include using namespace std;typedef long long ll;const int P = 998244353;const int N =110;int n,m;int v[N][N],w[N][N],s[N];int dp[N];int main() { cin>>n>>m; for(int i = 1;i>s[i]; for(int j = 0;j>v[i][j]>>w[i][j]; } for(int i = 1; i = 0; j--) { // 逆序遍历容量（关键：避免组内物品重复选择） for(int k = 0; k < s[i]; k++) { // 枚举组内每个物品 // 若当前物品体积不超过容量j，更新dp[j] if(v[i][k] <= j) { dp[j] = max(dp[j], dp[j - v[i][k]] + w[i][k]); } } }} cout<<dp[m]; return 0;}