网站导航
> 技术文档 > #Datawhale 组队学习#强化学习Task4

#Datawhale 组队学习#强化学习Task4

网友: 技术文档 2025-07-26 21:03:31

强化学习Task1：#Datawhale组队学习#7月-强化学习Task1-CSDN博客

强化学习Task2:#Datawhale组队学习#7月-强化学习Task2-CSDN博客

本篇是Task4：对应教材的第七章DQN算法，第八章DQN算法进阶

第七章DQN算法

 DQN (Deep Q-Network)是深度学习和强化学习结合的第一个重大突破，也是现代深度强化学习的基石。其是在Q-learning算法的基础上引入神经网络来近似Q函数，从而能够处理高维的状态空间。

7.1深度网络

传统Q表是一个二维表格，只能处理离散的状态和动作空间，而神经网络则可以处理连续的状态和动作空间。在Q表中我们描述状态空间的时候一般用的是状态个数，而在神经网络中我们用的是状态维度。

DQN算法的核心部分，即如何用神经网络来近似Q函数，以及如何用梯度下降的方式来更新网络参数。

7.2经验回放

在DQN中，我们会把每次与环境交互得到的样本都存储在一个经验回放中，然后每次从经验池中随机抽取一批样本来训练网络。

 这样做的好处是，首先每次迭代的样本都是从经验池中随机抽取的，因此每次迭代的样本都是近似独立同分布的，这样就满足了梯度下降法的假设。其次，经验池中的样本是从环境中实时交互得到的，因此每次迭代的样本都是相互关联的，这样的方式相当于是把每次迭代的样本都进行了一个打乱的操作，这样也能够有效地避免训练的不稳定性。

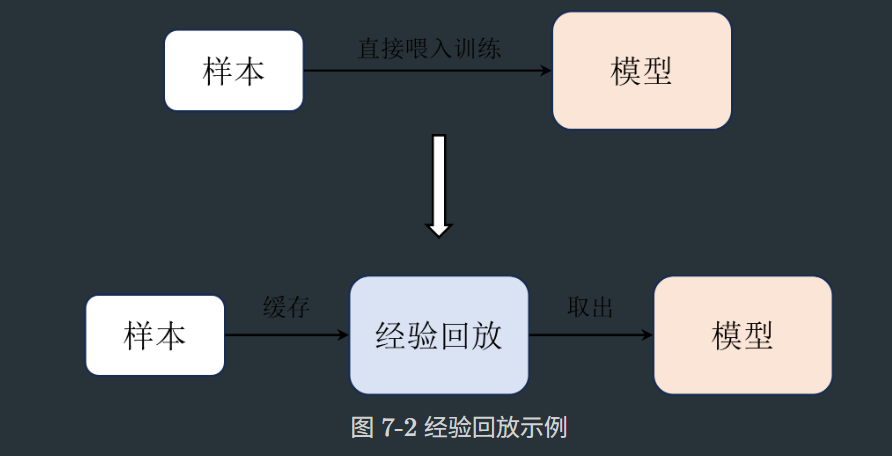
经验回放的容量是需要有一定的容量限制的。本质上是因为在深度学习中我们拿到的样本都是事先准备好的，即都是很好的样本，但是在强化学习中样本是由智能体生成的，在训练初期智能体生成的样本虽然能够帮助它朝着更好的方向收敛，但是在训练后期这些前期产生的样本相对来说质量就不是很好了，此时把这些样本喂入智能体的深度网络中更新反而影响其稳定。这就好比我们在小学时积累到的经验，会随着我们逐渐长大之后很有可能就变得不是很适用了，所以经验回放的容量不能太小，太小了会导致收集到的样本具有一定的局限性，也不能太大，太大了会失去经验本身的意义。

解决问题：

  1. 数据相关性：连续样本高度相关 → 导致SGD不稳定

  2. 数据利用率低：用后即弃 → 样本效率低

  3. 非平稳分布：策略更新导致数据分布漂移

为什么有效：

  • 相当于在历史数据分布上训练 → 更接近独立同分布（i.i.d）

  • 重用旧经验 → 样本效率提升10倍以上（Nature论文结论）

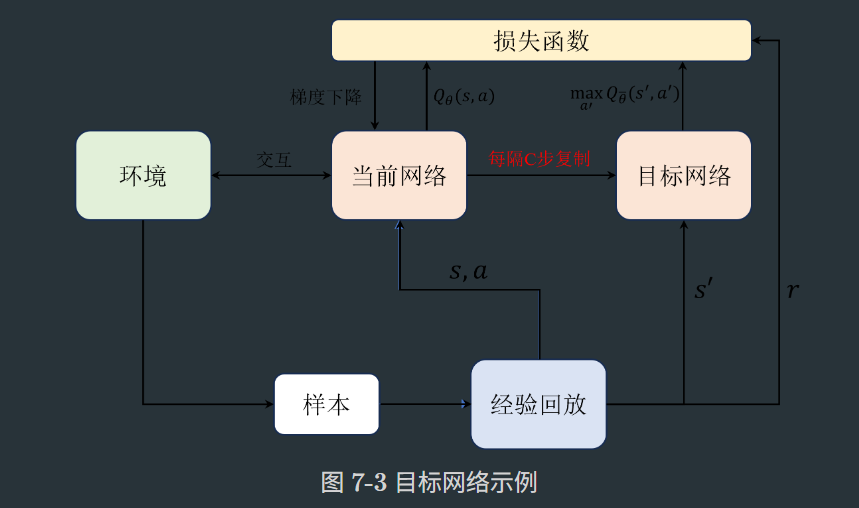
7.3目标网络

问题分析：

在Q-Learning中，目标值计算公式为：y = r + γ * max_a\' Q(s\', a\'; θ)

由于目标值计算与当前Q网络共享参数θ，导致在更新θ时目标值会同步变化，从而引发训练过程中的震荡和发散问题。

解决方案：

引入独立的目标网络Q(s, a; θ⁻)，保持参数θ⁻与主网络参数θ分离。

改进后的目标值计算公式：y = r + γ * max_a\' Q(s\', a\'; θ⁻)

目标网络和当前网络结构都是相同的，都用于近似Q值，在实践中每隔若干步才把每步更新的当前网络参数复制给目标网络，这样做的好处是保证训练的稳定，避免Q值的估计发散。

7.4实战DQN算法

伪代码：

以下是一个完整的 DQN 实现方案，包含代码实现、调试技巧和训练策略 。

完整 DQN 实现（PyTorch）（参考大模型辅助生成）

import gymimport numpy as npimport torchimport torch.nn as nnimport torch.optim as optimimport torch.nn.functional as Ffrom collections import deque, namedtupleimport randomimport matplotlib.pyplot as plt# 设置随机种子保证可复现SEED = 42random.seed(SEED)np.random.seed(SEED)torch.manual_seed(SEED)# 定义经验元组Experience = namedtuple(\'Experience\', (\'state\', \'action\', \'reward\', \'next_state\', \'done\'))class ReplayBuffer: \"\"\"经验回放缓冲区\"\"\" def __init__(self, capacity): self.buffer = deque(maxlen=capacity) # 环形队列 def __len__(self): return len(self.buffer) def add(self, state, action, reward, next_state, done): \"\"\"添加新经验\"\"\" self.buffer.append(Experience(state, action, reward, next_state, done)) def sample(self, batch_size): \"\"\"随机采样一批经验\"\"\" experiences = random.sample(self.buffer, batch_size) # 转换为PyTorch张量 states = torch.tensor([e.state for e in experiences], dtype=torch.float32) actions = torch.tensor([e.action for e in experiences], dtype=torch.int64) rewards = torch.tensor([e.reward for e in experiences], dtype=torch.float32) next_states = torch.tensor([e.next_state for e in experiences], dtype=torch.float32) dones = torch.tensor([e.done for e in experiences], dtype=torch.float32) return states, actions, rewards, next_states, donesclass QNetwork(nn.Module): \"\"\"Q网络模型\"\"\" def __init__(self, state_size, action_size, hidden_size=64): super(QNetwork, self).__init__() self.fc1 = nn.Linear(state_size, hidden_size) self.fc2 = nn.Linear(hidden_size, hidden_size) self.fc3 = nn.Linear(hidden_size, action_size) def forward(self, state): x = F.relu(self.fc1(state)) x = F.relu(self.fc2(x)) return self.fc3(x)class DQNAgent: \"\"\"DQN智能体\"\"\" def __init__(self, state_size, action_size): self.state_size = state_size self.action_size = action_size # 超参数 self.buffer_size = 10000 self.batch_size = 64 self.gamma = 0.99 # 折扣因子 self.lr = 0.001 # 学习率 self.tau = 0.005 # 软更新系数 self.epsilon = 1.0 # 初始探索率 self.epsilon_min = 0.01 self.epsilon_decay = 0.995 # 网络初始化 self.q_network = QNetwork(state_size, action_size) self.target_network = QNetwork(state_size, action_size) self.target_network.load_state_dict(self.q_network.state_dict()) # 优化器 self.optimizer = optim.Adam(self.q_network.parameters(), lr=self.lr) # 经验回放 self.memory = ReplayBuffer(self.buffer_size) # 训练统计 self.losses = [] self.rewards = [] def select_action(self, state): \"\"\"ε-贪心策略选择动作\"\"\" if np.random.rand() <= self.epsilon: return np.random.choice(self.action_size) # 随机探索 else: state = torch.tensor(state, dtype=torch.float32).unsqueeze(0) with torch.no_grad(): q_values = self.q_network(state) return torch.argmax(q_values).item() # 选择最大Q值动作 def update_epsilon(self): \"\"\"衰减探索率\"\"\" self.epsilon = max(self.epsilon_min, self.epsilon * self.epsilon_decay) def learn(self): \"\"\"从经验中学习更新网络\"\"\" if len(self.memory) = 195:  print(f\"Solved in {episode+1} episodes!\")  return print(\"Training completed!\") def plot_results(self): \"\"\"绘制训练结果\"\"\" plt.figure(figsize=(12, 5)) # 奖励曲线 plt.subplot(1, 2, 1) plt.plot(self.rewards, label=\'Episode Reward\') plt.plot(self.moving_average(self.rewards, 50), \'r-\', label=\'Moving Avg (50)\') plt.xlabel(\'Episode\') plt.ylabel(\'Reward\') plt.title(\'Training Rewards\') plt.legend() # 损失曲线 plt.subplot(1, 2, 2) plt.plot(self.losses) plt.xlabel(\'Learning Step\') plt.ylabel(\'Loss\') plt.title(\'Training Loss\') plt.tight_layout() plt.show() def moving_average(self, data, window_size): \"\"\"计算移动平均\"\"\" return np.convolve(data, np.ones(window_size)/window_size, mode=\'valid\')# 创建环境和智能体env = gym.make(\'CartPole-v1\')state_size = env.observation_space.shape[0]action_size = env.action_space.nagent = DQNAgent(state_size, action_size)# 开始训练agent.train(env, episodes=500)# 保存模型torch.save(agent.q_network.state_dict(), \'dqn_cartpole.pth\')# 绘制结果agent.plot_results()# 测试训练好的智能体def test_agent(env, agent, episodes=10, render=True): \"\"\"测试训练好的智能体\"\"\" total_rewards = [] for episode in range(episodes): state = env.reset() total_reward = 0 done = False while not done: if render: env.render() action = agent.select_action(state) state, reward, done, _ = env.step(action) total_reward += reward total_rewards.append(total_reward) print(f\"Test Episode {episode+1}: Reward = {total_reward}\") print(f\"Average Test Reward: {np.mean(total_rewards):.2f}\") env.close()# 加载模型进行测试agent.q_network.load_state_dict(torch.load(\'dqn_cartpole.pth\'))agent.epsilon = 0.01 # 设置较低的探索率test_agent(env, agent, episodes=10)

7.5习题

1. 相比于Q-learning算法，DQN算法做了哪些改进？

DQN算法在Q-learning的基础上主要引入了两项关键改进：一是使用深度神经网络作为函数近似器，以处理高维状态输入（如Atari游戏中的像素图像）；二是增加了经验回放机制和目标网络结构。经验回放通过存储和随机采样历史经验（即状态、动作、奖励、下一状态）来打破数据间的相关性，而目标网络通过定期更新其参数（而非每一步）来稳定目标Q值的计算，从而减少训练过程中的振荡和发散风险。这些改进使DQN能够更高效地学习复杂环境中的策略。

2. 为什么要在DQN算法中引入 ε—greedy策略？

在DQN算法中引入 ε—greedy策略是为了平衡探索（exploration）和利用（exploitation）。具体来说，ε—greedy策略以概率 εε 随机选择动作（探索新状态），以概率 1−ε 选择当前Q值最大的动作（利用已知最优动作）。这避免了算法过早收敛到次优策略，确保在训练初期充分探索环境，从而发现潜在的高奖励路径。例如，在游戏学习中，随机探索能帮助智能体尝试不同动作，避免陷入局部最优。

3. DQN算法为什么要多加一个目标网络？

DQN算法采用目标网络主要是为了解决训练不稳定的问题。在标准Q-learning中，目标Q值使用与当前网络相同的参数计算，导致目标值随训练快速变化，容易引起振荡或发散。目标网络是当前网络的副本，其参数定期更新（例如每1000步同步一次），而非每一步更新。这样，目标Q值在短期内保持相对稳定，减少了目标与估计值之间的相关性波动，使训练过程更平滑、收敛更快。

4. 经验回放的作用是什么？

经验回放的作用是提高训练效率和稳定性。它将智能体的经验（状态、动作、奖励、下一状态）存储在回放缓冲区中，并在训练时随机采样小批量经验进行学习。这样做有三个主要好处：一是打破数据间的时间相关性，减少方差；二是允许同一经验被多次复用，提高样本效率；三是通过随机采样避免过拟合当前策略，使学习更鲁棒。例如，在连续控制任务中，经验回放能帮助智能体从历史数据中泛化，加速收敛。

第八章DQN算法进阶

基础的DQN算法存在一些局限性，所以需要基于此做一些改进，以提高算法性能。

8.1 Double DQN 算法

Double DQN (DDQN) 算法这是DQN最重要的改进之一，旨在解决基础DQN中存在的Q值高估问题。主要贡献是通过引入两个网络用于解决Q值过估计的问题。把动作选择和动作评估这两个过程分离开来，从而减轻了过估计问题。

Double DQN (DDQN) 通过一个简单而深刻的洞见——使用在线网络选择动作，使用目标网络评估该动作的价值——有效地解耦了动作选择和动作价值评估这两个关键步骤。这种解耦打破了基础DQN中由于使用同一个有偏差的估计源（目标网络）进行这两项任务所导致的系统性高估循环。DDQN实现成本低，效果显著，是DQN系列算法中应用最广泛、最基础也最重要的改进之一，几乎成为了现代DQN实现的标配组件。

8.2 Dueling DQN 算法

Dueling DQN的核心思想是将Q网络分解为两个独立的、并行计算的流（Stream）。

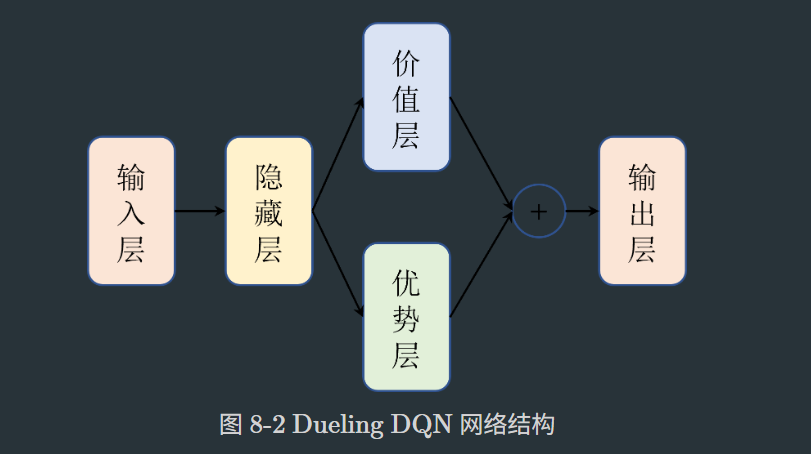
Dueling DQN通过创新性地将Q网络分解为状态价值流和动作优势流，并引入优势中心化技巧，有效解决了基础DQN中状态价值信息分散和动作优势学习困难的问题。其核心优势在于：

  • 解耦学习：独立学习状态价值和动作优势，减少冗余。

  • 高效表示：更擅长处理状态价值主导或动作优势微妙的场景。

  • 泛化提升：学习到的状态价值特征具有更好的泛化能力。

  • 易于集成：架构改进与Double DQN、PER等其他DQN进阶算法正交兼容。

Dueling DQN是深度强化学习中网络架构设计的一个典范，其思想简洁而深刻，在实践中被证明非常有效，并成为后续许多先进算法（如Rainbow）的核心组件之一。理解Dueling DQN是掌握深度Q学习进阶技术的关键。

8.3 Noisy DQN 算法

Noisy DQN的核心思想非常新颖：将噪声直接添加到Q网络的权重参数上，并使这些噪声参数可以通过梯度下降进行学习和调整。

Noisy DQN 通过一个巧妙的机制——将可学习的噪声注入Q网络的参数中，并在每次前向传播时重新采样这些噪声——革命性地替代了传统的 ε-greedy 探索。其核心价值在于实现了：

  • 自适应探索： 噪声强度 σ 通过梯度下降学习调整，实现“有把握时少探索，没把握时多探索”。

  • 状态相关探索： 探索行为由输入状态 s 和网络当前的学习状态共同决定，探索更加智能和高效。

  • 简化流程： 消除了手动调整 ε 衰减策略的繁琐过程。

Noisy DQN 不仅显著提升了DQN在复杂环境中的探索效率和最终性能，更重要的是，它提供了一种将探索机制深度集成到神经网络学习过程中的通用范式，这一思想对强化学习领域产生了深远影响。理解 Noisy DQN 是掌握现代深度强化学习探索技术的关键一步。

8.4 PER DQN 算法

DQN算法通常使用经验回放来提高算法的性能，即通过存储智能体与环境交互的经验，然后从中随机采样一批样本用于训练。这样做的好处是可以减少样本之间的相关性，从而提高训练的效率和稳定性。然而，这样的经验回放也会存在一个问题，即它采用的是均匀采样和批量更新的方法，这就导致一些特别少但是价值可能特别高的经验或者样本没有被高效地利用到，从而影响算法的收敛性。

PER DQN算法提出了一种新的经验回放，即优先经验回放，通过引入优先级采样的方法，使得经验回放中的样本可以根据其重要性来进行采样，这样不仅能提升算法的效果，还可以加快学习速度。

Prioritized Experience Replay (PER) DQN 通过根据经验样本的学习潜力（主要由TD误差绝对值衡量）赋予不同的采样优先级，革命性地改进了DQN的经验回放机制。其核心贡献在于：

  • 高效采样： 利用 SumTree 数据结构实现 O(log n) 时间复杂度的优先级采样。

  • 重要性采样校正： 通过引入重要性采样权重 w_i 和 β 调度策略，有效减轻了非均匀采样引入的偏差。

  • 显著提升： 在样本效率和最终性能上通常带来质的飞跃，尤其在包含稀疏或关键事件的环境中。

8.5 C51 算法

C51算法是一种值分布强化学习算法。C51 的核心思想是：不再让神经网络输出一个标量Q值，而是让它输出状态-动作对 (s, a) 的累积回报 Z(s, a) 的离散概率分布。

C51 (Categorical DQN) 算法是深度强化学习从期望值学习迈向分布学习的关键一步。其核心贡献在于：

  • 分布建模： 将累积回报 Z(s, a) 建模为在固定离散支撑点上的概率分布。

  • 投影贝尔曼更新： 设计了一种将贝尔曼算子作用后的分布投影回固定支撑点的方法（通过线性插值）。

  • 分布匹配损失： 使用KL散度/交叉熵损失最小化预测分布和目标分布的距离。

尽管存在计算开销和超参数敏感性的挑战，C51 在理论和实践中都证明了直接学习价值分布的优势：它提供了更丰富的信息表达、更强的学习信号，并最终在性能上超越了仅预测期望值的算法。

Rainbow DQN 算法。这是DeepMind在2017年提出的一个集成性工作，将当时六大DQN改进算法融合到一个框架中，在Atari游戏上实现了最先进（SOTA）的性能。Rainbow不仅展示了这些改进的互补性，也为深度强化学习的算法设计提供了重要范例。

组件 原论文对应算法 解决的核心问题 1. Double DQN Double DQN (2015) Q值高估（解耦动作选择与价值评估） 2. Prioritized Experience Replay (PER) Prioritized DQN (2015) 经验回放的采样效率（优先学习高TD误差样本） 3. Dueling Networks Dueling DQN (2016) 状态价值与动作优势的解耦学习 4. Multi-step Learning — 单步TD的偏差问题（折中MC和TD） 5. Distributional RL (C51) Categorical DQN (2017) 回报的分布建模（超越期望值） 6. Noisy Nets Noisy DQN (2017) 探索效率（替代ε-greedy）

8.6习题

1. DQN 算法为什么会产生 Q 值的过估计问题？
DQN 算法产生 Q 值过估计问题的核心原因在于目标值计算方式与函数近似误差的共同作用。具体来说，算法在计算目标 Q 值时使用公式：即时奖励 + 折扣因子 × 目标网络对下一状态的最大 Q 估计值。其中 最大化操作（max） 会优先选择被高估的动作值（即使存在估计误差），而深度神经网络对动作价值的估计存在正向偏差时，该偏差会被 max 操作放大。这种高估值会通过训练更新传回当前网络，形成 自增强循环，导致 Q 值系统性高于真实值。例如：多人估算商品价格时，若直接采用最高估价作为\"真实值\"，会导致整体定价虚高。

2. 同样是提高探索，Noisy DQN 和 ε-greedy 策略有什么区别？
两者的本质区别在于探索机制的设计层级：

  • ε-greedy 在 动作选择层 引入探索：以固定概率 ε 完全随机选择动作（无论动作优劣），其余情况选择最优动作。这种方式 与状态无关，可能重复尝试低价值动作，探索效率较低。

  • Noisy DQN 在 网络参数层 引入探索：通过向神经网络权重注入随机噪声（如高斯噪声），使所有动作的 Q 值计算产生 定向扰动。智能体仍选择扰动后 Q 值最大的动作，但噪声会导致不同状态下探索强度 自适应变化。例如：当某动作真实价值接近最优值时，噪声扰动更容易使其被选中，实现 高效定向探索。
    简言之：ε-greedy 是盲目的均匀探索，而 Noisy DQN 是通过参数扰动实现的智能探索。

好了，本次就写到这里。码字不易，点赞收藏关注吧。

网络标签：

相关问题