扩散模型原理学习记录【最大似然估计到KL散度的推导过程】

技术文档

扩散模型原理学习记录【最大似然估计到KL散度的推导过程】
这个公式展示了如何通过最大似然估计（Maximum Likelihood Estimation, MLE）来学习模型参数 (\\theta)，并最终将其与KL散度（Kullback-Leibler Divergence）联系起来。以下是每一步的详细解释：

1. 从数据中采样

$Pdata(x)\\text{Sample } \\{x^1, x^2, ..., x^m\\} \\text{ from } P_{data}(x)$
- 这是最大似然估计的起点。我们从真实数据分布 $P_{data}(x)$ ) 中独立采样得到 $(m$ ) 个样本 ${x^1, x^2, ..., x^m\\}$ )。

2. 最大似然估计的目标

$θ∗=arg⁡max⁡θ∏i=1mPθ(xi)\\theta^* = \\arg \\max_{\\theta} \\prod_{i=1}^m P_\\theta(x^i)$

目标是找到参数 $(θ(\\theta$ )，使得在这些样本下，模型分布 $(Pθ(x)(P_\\theta(x)$ ) 的联合概率（似然函数）最大。
直接优化乘积形式可能数值不稳定，因此通常转换为对数似然。

3. 转换为对数似然

$θ∗=arg⁡max⁡θlog⁡∏i=1mPθ(xi)=arg⁡max⁡θ∑i=1mlog⁡Pθ(xi)\\theta^* = \\arg \\max_{\\theta} \\log \\prod_{i=1}^m P_\\theta(x^i) = \\arg \\max_{\\theta} \\sum_{i=1}^m \\log P_\\theta(x^i)$

对数函数是单调递增的，优化对数似然等价于优化原始似然。
乘积转换为求和，简化计算。

4. 用期望近似求和

$θ∗≈arg⁡max⁡θEx∼Pdata[log⁡Pθ(x)]\\theta^* \\approx \\arg \\max_{\\theta} E_{x \\sim P_{data}}[\\log P_\\theta(x)]$

当样本数量 (m) 很大时，求和可以用期望近似：
$1m∑i=1mlog⁡Pθ(xi)≈Ex∼Pdata[log⁡Pθ(x)].\\frac{1}{m} \\sum_{i=1}^m \\log P_\\theta(x^i) \\approx E_{x \\sim P_{data}}[\\log P_\\theta(x)].$
最大化期望对数似然等价于最大化原始目标。

这里 $P_\\theta(x^i)$ 是值， $P_{data}(x)$ 是前面那个值对应的概率，当样本量足够大的时候，样本均值收敛于期望值，为什么概率是 $P_{data}(x)$ ，因为这是x在真实世界采样的概率，就是x会出现的概率。

5. 引入KL散度

$θ∗=arg⁡max⁡θ∫xPdata(x)log⁡Pθ(x)dx−∫xPdata(x)log⁡Pdata(x)dx\\theta^* = \\arg \\max_{\\theta} \\int_x P_{data}(x) \\log P_\\theta(x) dx - \\int_x P_{data}(x) \\log P_{data}(x) dx$

第一项是期望对数似然 $(Ex∼Pdata[log⁡Pθ(x)](E_{x \\sim P_{data}}[\\log P_\\theta(x)]$ )，就是期望的定义嘛，样本值和样本概率的积分。
第二项是真实分布 $P_{data}(x)$ ) 的熵，与 $(θ(\\theta$ ) 无关，因此可以忽略，对于 $(θ(\\theta$ ) 的优化没有影响，因此可以添加，为了后面的转化。
通过加减这一项，可以将问题重新表述为KL散度的形式。

6. 转换为KL散度的最小化

$θ∗=arg⁡max⁡θ∫xPdata(x)log⁡Pθ(x)Pdata(x)dx=arg⁡min⁡θKL(Pdata∥Pθ)\\theta^* = \\arg \\max_{\\theta} \\int_x P_{data}(x) \\log \\frac{P_\\theta(x)}{P_{data}(x)} dx = \\arg \\min_{\\theta} KL(P_{data} \\| P_\\theta)$

比值 $(log⁡Pθ(x)Pdata(x)(\\log \\frac{P_\\theta(x)}{P_{data}(x)}$ ) 是KL散度的核心部分。
KL散度的定义为：
$KL(Pdata∥Pθ)=∫xPdata(x)log⁡Pdata(x)Pθ(x)dx.KL(P_{data} \\| P_\\theta) = \\int_x P_{data}(x) \\log \\frac{P_{data}(x)}{P_\\theta(x)} dx.$
最大化对数似然等价于最小化 $(KL(Pdata∥Pθ)(KL(P_{data} \\| P_\\theta)$ )，即让模型分布 $(Pθ(P_\\theta$ ) 尽可能接近真实分布 (P_{data})。

总结

核心思想：通过最大似然估计，模型参数 (\\theta) 的学习过程可以转化为最小化真实分布 (P_{data}) 和模型分布 (P_\\theta) 之间的KL散度。
KL散度的意义：衡量两个分布之间的差异，最小化KL散度意味着让模型分布逼近真实分布。
实际应用：在生成模型（如VAE、GAN）中，KL散度是衡量生成分布与真实分布差异的重要工具。

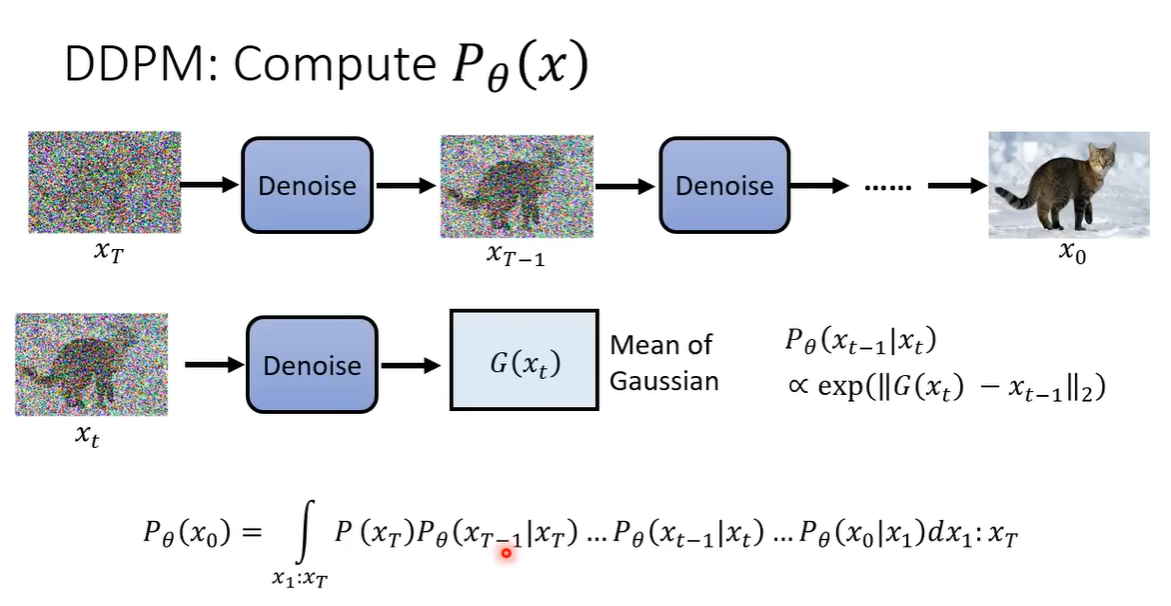
扩散模型原理学习记录【最大似然估计到KL散度的推导过程】
这张图描述了扩散概率模型（DDPM）中生成数据 ( x_0 ) 的概率 ( P_\\theta(x_0) ) 的计算过程。以下是逐步解析：

1. DDPM 的核心思想

DDPM（Denoising Diffusion Probabilistic Models）通过逐步去噪的方式生成数据。其核心是定义一个前向扩散过程（逐步加噪）和反向去噪过程（逐步生成）。

2. 前向与反向过程

前向过程（扩散过程）：
逐步将数据 $x_0$ ) 加噪，直到变为纯噪声 $x_T$ 。
- 每一步的转移概率为 $q(x_t|x_{t-1})$ )，通常定义为高斯分布。
反向过程（生成过程）：
从噪声 $x_T$ ) 开始，逐步去噪生成数据 $x_0$ )。
- 每一步的转移概率为 $P_\\theta(x_{t-1}|x_t)$ )，由神经网络 $G(x_t)$ ) 学习。

3. 生成概率 $P_\\theta(x_0)$ ) 的计算

图中给出了生成 $x_0$ ) 的概率的积分形式：
$dx1⋯dxTP_\\theta(x_0) = \\int_{x_1 \\cdots x_T} P(x_T) P_\\theta(x_{T-1}|x_T) \\cdots P_\\theta(x_0|x_1) \\, dx_1 \\cdots dx_T$

$P(x_T)$ )：初始噪声分布（通常是标准高斯分布 $\\mathcal{N}(0, I)$ )）。
$P_\\theta(x_{t-1}|x_t)$ )：反向过程的每一步去噪概率，由神经网络 $G(x_t)$ ) 建模。
积分路径：对所有可能的中间状态 $x_1$ ) 到 $x_T$ ) 进行积分。

4. 反向过程的转移概率 $P_\\theta(x_{t-1}|x_t)$ )

图中提到：
$Pθ(xt−1∣xt)∝αexp⁡(−∥G(xt)−xt−1∥2)P_\\theta(x_{t-1}|x_t) \\propto \\alpha \\exp\\left(-\\|G(x_t) - x_{t-1}\\|_2\\right)$

$G(x_t)$ )：去噪网络的输出，通常是 $x_{t-1}$ ) 的均值。
高斯分布假设：实际中， $P_\\theta(x_{t-1}|x_t)$ ) 通常定义为高斯分布：
$Pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))P_\\theta(x_{t-1}|x_t) = \\mathcal{N}\\left(x_{t-1}; \\mu_\\theta(x_t, t), \\Sigma_\\theta(x_t, t)\\right)$
其中均值 $\\mu_\\theta(x_t, t)$ ) 由网络预测，方差 $\\Sigma_\\theta(x_t, t)$ ) 可以是固定的或学习的。

5. 去噪网络 $G(x_t)$ ) 的作用

输入：噪声数据 $x_t$ ) 和时间步 $(t$ )。
输出：预测去噪后的数据 $x_{t-1}$ ) 或其均值。
训练目标：最小化预测与真实去噪结果的误差（如均方误差）。

6. 关键点总结

生成过程：通过从噪声 $x_T$ ) 逐步去噪（ $x_T \\to x_{T-1} \\to \\cdots \\to x_0$ )）生成数据。
概率计算：生成 $x_0$ ) 的概率是所有可能路径的积分。
网络建模：去噪步骤 $P_\\theta(x_{t-1}|x_t)$ ) 由神经网络学习，通常假设为高斯分布。

数学补充

在实际训练中，DDPM 通过优化以下变分下界（ELBO）来学习去噪网络：
$L=Eq(x1:T∣x0)[log⁡q(x1:T∣x0)Pθ(x0:T)]\\mathcal{L} = \\mathbb{E}_{q(x_{1:T}|x_0)} \\left[ \\log \\frac{q(x_{1:T}|x_0)}{P_\\theta(x_{0:T})} \\right]$
其中 $P_\\theta(x_{0:T})$ ) 是联合生成分布， $q(x_{1:T}|x_0)$ ) 是前向扩散分布。

图示改进建议

若需完善此图，可补充：

前向扩散过程的示意图（从 $x_0$ ) 到 $x_T$ )）。
去噪网络 $G(x_t)$ ) 的详细结构（如U-Net）。
时间步$( t $) 对去噪过程的影响。

扩散模型原理学习记录【最大似然估计到KL散度的推导过程】

1. 从数据中采样

2. 最大似然估计的目标

3. 转换为对数似然

4. 用期望近似求和

这里 $P_\\theta(x^i)$ 是值， $P_{data}(x)$ 是前面那个值对应的概率，当样本量足够大的时候，样本均值收敛于期望值，为什么概率是 $P_{data}(x)$ ，因为这是x在真实世界采样的概率，就是x会出现的概率。

5. 引入KL散度

6. 转换为KL散度的最小化

总结

1. DDPM 的核心思想

2. 前向与反向过程

3. 生成概率 $P_\\theta(x_0)$ ) 的计算

4. 反向过程的转移概率 $P_\\theta(x_{t-1}|x_t)$ )

5. 去噪网络 $G(x_t)$ ) 的作用

6. 关键点总结

数学补充

图示改进建议

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

扩散模型原理学习记录【最大似然估计到KL散度的推导过程】

1. 从数据中采样

2. 最大似然估计的目标

3. 转换为对数似然

4. 用期望近似求和

5. 引入KL散度

6. 转换为KL散度的最小化

总结

1. DDPM 的核心思想

2. 前向与反向过程

3. 生成概率 (Pθ(x0)( P_\\theta(x_0)(Pθ​(x0​)) 的计算

4. 反向过程的转移概率 (Pθ(xt−1∣xt)( P_\\theta(x_{t-1}|x_t)(Pθ​(xt−1​∣xt​))

5. 去噪网络 (G(xt)( G(x_t)(G(xt​)) 的作用

6. 关键点总结

数学补充

图示改进建议

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

3. 生成概率 $P_\\theta(x_0)$ ) 的计算

4. 反向过程的转移概率 $P_\\theta(x_{t-1}|x_t)$ )

5. 去噪网络 $G(x_t)$ ) 的作用